
- •Министерство образования и науки российской федерации
- •Дифференциальные уравнения первого порядка
- •Уравнения с разделёнными и разделяющимися переменными
- •Однородные уравнения первого порядка
- •Линейные уравнения первого порядка
- •Уравнение в полных дифференциалах
- •Интегрирующий множитель
- •Дифференциальные уравнения высших порядков
- •Уравнения вида
- •Уравнения второго порядка, приводящиеся к уравнениям первого порядка
- •Линейные однородные уравнения. Определения и общие свойства
- •Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения го порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения второго порядка
- •Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения высших порядков
- •Системы обыкновенных дифференциальных уравнений
- •Системы линейных дифференциальных уравнений с постоянными коэффициентами
- •Р я д ы Числовые ряды Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакопеременные ряды
- •Функциональные ряды
- •Ряды Тейлора и Маклорена
- •Ряды Фурье
- •Ряды Фурье для четных и нечетных функций
- •Ряд Фурье для функции с периодом
- •К о м б и н а т о р и к а
- •Общие правила комбинаторики
- •Соединения в комбинаторике
- •Размещения без повторений
- •Перестановки без повторений
- •Сочетания без повторений
- •Размещения с повторениями
- •11 12 13 14 15 16 17 19
- •Перестановки с повторениями
- •Т е о р и я в е р о я т н о с т е й Случайные события Основные понятия теории вероятностей
- •Основные теоремы теории вероятностей Теорема сложения вероятностей несовместных событий
- •Зависимые и независимые события. Условная вероятность
- •Теорема умножения вероятностей
- •Теорема сложения вероятностей совместных событий
- •Вероятность появления хотя бы одного события
- •. Формула полной вероятности
- •Формула Бейеса
- •Повторение испытаний
- •Формула Бернулли
- •Локальная теорема Лапласа
- •. Формула Пуассона
- •Интегральная теорема Лапласа
- •Случайные величины Случайная величина. Виды случайных величин
- •Закон распределения вероятностей дискретной случайной величины
- •Числовые характеристики дискретных случайных величин
- •Математическое ожидание дискретной случайной величины
- •Дисперсия дискретной случайной величины
- •Плотность распределения вероятностей непрерывной случайной величины
- •Числовые характеристики непрерывных случайных величин
- •Законы распределений
- •Равномерное распределение
- •Нормальное распределение
- •. Правило трёх сигм
- •Показательное распределение
- •Функция надёжности
- •Элементы математической статистики Основные сведения из математической статистики
- •Статистическое распределение выборки. Полигон и гистограмма
- •1 4 6
- •10 15 25
- •Статистические оценки параметров распределения
- •Оценка генеральной дисперсии по исправленной выборочной
- •Точность оценки, доверительная вероятность (надёжность). Доверительный интервал
- •Методы расчёта сводных характеристик выборки
- •Сведение первоначальных вариант к равноотстоящим
- •Оценка отклонения теоретического и эмпирического распределений от нормального. Асимметрия и эксцесс
- •Элементы теории корреляции
- •. (1)
- •(4) . (5) Корреляционная таблица
- •Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным
- •Методика вычисления выборочного коэффициента корреляции
- •. Статистическая проверка статистических гипотез
- •Линейное программирование Задача линейного программирования
- •Построение математической модели
- •Графическое решение задачи линейного программирования
- •Симплексный метод решения задачи линейного программирования
- •Решение задачи 1 симплексным методом
- •Искусственное начальное решение. Метод больших штрафов.
- •Особые случаи применения симплекс-метода
- •1.7.2 Бесконечное множество решений
- •1.7.4 Неограниченные решения
- •1.7.5 Промежуточное вырожденное решение
- •Задача о назначениях
- •4 Изменение запаса ресурса продукта а 7
- •1 Изменение единицы стоимости продукта а 4
- •Заключение
Числовые характеристики дискретных случайных величин
Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться числами, которые описывают случайную величину суммарно. Такие числа называют числовыми характеристиками случайной величины. К ним относятся: математическое ожидание, дисперсия.
Математическое ожидание дискретной случайной величины
Математическим
ожиданием
дсв называют сумму произведений всех
её возможных значений на их вероятности
и обозначается
 .
.
Если дсв задана законом распределения

 , то
, то

Пусть произведено
 испытаний, в которых случайная величина
испытаний, в которых случайная величина приняла
приняла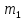 раз значение
раз значение ,
, раз значение
раз значение ,
…,
,
…, раз значение
раз значение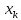 ,
причём
,
причём +
+ +…+
+…+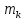 =
= .
Тогда сумма всех значений, принятых
.
Тогда сумма всех значений, принятых , равна
, равна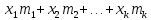 .
Найдём среднее арифметическое
.
Найдём среднее арифметическое всех значений
всех значений .
Итак,
.
Итак,
 .
Вероятностный смысл полученного
результата таков: математическое
ожидание приближённо равно среднему
арифметическому наблюдаемых значений
случайной величины.
.
Вероятностный смысл полученного
результата таков: математическое
ожидание приближённо равно среднему
арифметическому наблюдаемых значений
случайной величины.
Математическое ожидание обладает следующими свойствами:
Математическое ожидание постоянной величины равно самой постоянной, т.е.

В
самом деле, постоянную можно рассмотреть
как дискретную случайную величину,
которая имеет одно возможное значение
 и принимает его с вероятностью
и принимает его с вероятностью .
.



Постоянный множитель можно выносить за знак математического ожидания, т.е.
 .
.
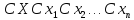

 .
.
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е.

Если
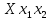
 , то
, то




Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых, т.е.
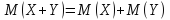 .
.
Если

 , то
, то





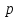





 +
+
 ,
т.к.
,
т.к.
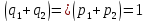 .
.
Математическое ожидание числа появлений события А в
 независимых испытаниях равно произведению
числа испытаний на вероятность появления
события в каждом испытаний, т.е.
независимых испытаниях равно произведению
числа испытаний на вероятность появления
события в каждом испытаний, т.е.
Дисперсия дискретной случайной величины
Математическое ожидание, или среднее значение, случайной величины в ряде вопросов является достаточной характеристикой изучаемой случайной величины. Но бывает так, что одно среднее значение не даёт практически исчерпывающей характеристики случайной величины, а требуется ещё знать, сколь велики отклонения отдельных значений случайной величины от её математического ожидания.
Например, по данным статистического наблюдения изучается: средний рост или вес человека в определённой группе. Результаты опыта или наблюдения может считаться удачным, если возможные значения случайной величины незначительно отличаются от математического ожидания. Поэтому возникает необходимость введения ещё понятия отклонения случайной величины от её математического ожидания.
Отклонением
называют разность между случайной
величиной и её математическим ожиданием:
 .
.
Это отклонение характеризует рассеяние случайной величины. На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение, т.е. математическое ожидание отклонения.
Покажем, что
математическое ожидание отклонения
равно нулю. В самом деле
 .
Это объясняется тем, что одни возможные
отклонения положительны, а другие –
отрицательны; в результате их взаимного
погашения среднее значение отклонения
равно нулю. Эти соображения говорят о
целесообразности заменить возможные
отклонения их абсолютными значениями
или их квадратами. В случае замены
абсолютными значениями приходится
оперировать с абсолютными величинами,
что приводит иногда к серьёзным
затруднениям. Поэтому чаще всего идут
по другому пути, вычисляют среднее
значение квадрата отклонения, которое
и называют дисперсией.
.
Это объясняется тем, что одни возможные
отклонения положительны, а другие –
отрицательны; в результате их взаимного
погашения среднее значение отклонения
равно нулю. Эти соображения говорят о
целесообразности заменить возможные
отклонения их абсолютными значениями
или их квадратами. В случае замены
абсолютными значениями приходится
оперировать с абсолютными величинами,
что приводит иногда к серьёзным
затруднениям. Поэтому чаще всего идут
по другому пути, вычисляют среднее
значение квадрата отклонения, которое
и называют дисперсией.
Дисперсией
дискретной
случайной величины называют математическое
ожидание квадрата отклонения случайной
величины от её математического ожидания
и обозначают
 .
Таким образом:
.
Таким образом:
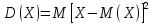
При решении
практических задач часто пользуются
немного видоизменённой формулой
дисперсии, а именно:
 .
При преобразовании было учтено, что
математическое ожидание
.
При преобразовании было учтено, что
математическое ожидание
 есть постоянная величина, а значит,
есть постоянная величина, а значит, есть также постоянные величины. Итак,
есть также постоянные величины. Итак,

Дисперсия обладает следующими свойствами:
Дисперсия постоянной величины равна нулю, т.е.
 .
.
В
самом деле
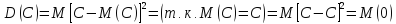 .
.
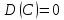 .
.
Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т.е.
 .
.
В
самом деле

 .
.
 .
.
Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин, т.е.



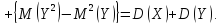

Дисперсия разности двух независимых случайных величин равна сумме их дисперсии, т.е.



Дисперсия числа появления события А в
 независимых испытаниях, в каждом из
которых вероятность
независимых испытаниях, в каждом из
которых вероятность появления события постоянна, равна
произведению числа испытаний на
вероятности появления и непоявления
события в одном испытании, т.е.
появления события постоянна, равна
произведению числа испытаний на
вероятности появления и непоявления
события в одном испытании, т.е. .
.
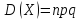 .
.
Среднее квадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг её среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Средним
квадратическим отклонением случайной
величины Х называется квадратный корень
из дисперсии и обозначается σ( :
:
 .
.
Легко показать, что
дисперсия имеет размерность, равную
квадрату размерности случайной величины.
Так как среднее квадратическое отклонение
равно квадратному корню из дисперсии,
то размерность σ(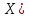 совпадает с размерностью случайной
величины. Поэтому в тех случаях, когда
желательно, чтобы оценка рассеяния
имела размерность случайной величины,
вычисляют среднее квадратическое
отклонение, а не дисперсию.
совпадает с размерностью случайной
величины. Поэтому в тех случаях, когда
желательно, чтобы оценка рассеяния
имела размерность случайной величины,
вычисляют среднее квадратическое
отклонение, а не дисперсию.
Функция распределения вероятностей случайной величины
Дискретная случайная величина может быть задана перечнем всех её возможных значений и их вероятностей. Такой способ задания не является общим: он не применим, например, для непрерывных случайных величин, так как в этом случае не предоставляется возможным перечислить все возможные значения. Поэтому вводят понятие функции распределения вероятностей случайной величины.
Пусть
 – действительное число. Вероятность
события, состоящего в том, что Х примет
значение, меньшее
– действительное число. Вероятность
события, состоящего в том, что Х примет
значение, меньшее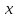 , т.е. вероятность события
, т.е. вероятность события ,
обозначим через
,
обозначим через .
.
Функцией
распределения
называется функция
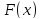 ,
определяющая вероятность того, что
случайная величин
,
определяющая вероятность того, что
случайная величин в результате испытания примет значение,
меньшее
в результате испытания примет значение,
меньшее ,
т.е.
,
т.е.
 .
.
Функция распределения обладает следующими свойствами:
 .
.Если
 ,
то
,
то .
.
В
самом деле, пусть
 .
Событие, состоящее в том, что
.
Событие, состоящее в том, что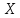 примет значение, меньшее
примет значение, меньшее ,
можно подразделить на два несовместных
события:
,
можно подразделить на два несовместных
события: примет значение, меньшее
примет значение, меньшее и
и примет значение, удовлетворяющее
неравенству
примет значение, удовлетворяющее
неравенству т.е.
т.е. ).
По теореме сложения имеем:
).
По теореме сложения имеем: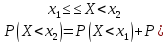 ),
откуда
),
откуда
 )
или
)
или
 .
Т.к. любая вероятность есть число
неотрицательное, то
.
Т.к. любая вероятность есть число
неотрицательное, то или
или .
.
Если
 и
и ,
то
,
то .
Таким образом, вероятность того, что
случайная величина примет значение,
заключённое в интервале
.
Таким образом, вероятность того, что
случайная величина примет значение,
заключённое в интервале ,
равна приращению функции распределения
на этом интервале:
,
равна приращению функции распределения
на этом интервале:

Если возможные значения случайной величины принадлежат интервалу
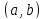 ,
то
,
то
а)
 ,
б)
,
б) .
График функции распределения непрерывной
случайной величины имеет вид:
.
График функции распределения непрерывной
случайной величины имеет вид:

