1.7.5 Промежуточное вырожденное решение

В отличие от случая 1.7.1 в данном случае на следующей итерации вырожденность уже не имеет места, причем значение целевой функции улучшается.

Пример 6. В стандартной форме

(1)

, (2)

, (3) ,

, (4)

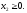(5)

Б	с				3	2	0		0		0				Замечания
	0		12		4	3	1		0		0		3		Признак вырожденности
	0		8		4	1	0		1		0		2
	0		8		4	-1	0		0		1		2
				0	-3	-2		0		0		0
	3		2		1		0				0		8		- вырожденное неоптимальное решение
	0		4		0	2	1		-1		0		2-min
	0		0		0	-2	0		-1		1		отр
				6	0	-		0				0
		3			1	0	-				0				- оптимальное вырожденное решение.
		2	2		0	1			-		0
		0	4		0	0	1		-2		1
					0	0						0

Задача о назначениях

Требуется распределить работ постанкам. Работа, выполнимая на станке, связана с затратами. Задача состоит в таком распределении работ по станкам ( одна работа выполняется одним станком ), которое соответствует минимуму суммарных затрат. Такая задача известна какзадача о назначениях.

Эту задачу можно рассматривать как частный случай транспортной задачи. Здесь работы представляют «исходные пункты», а станки – «пункты назначения». Предложение в каждом исходном пункте равно 1, т.е. .Аналогично спрос в каждом пункте назначения равен 1, т.е.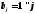. Стоимость «перевозки» (прикрепления) работык станкуравна. Если какую-либо работу нельзя выполнить на некотором станке, то соответствующая стоимостьберётся равной очень большому числу.

Общая структура задачи о назначениях имеет вид:

В случае существования дисбаланса, добавив фиктивные работы или станки в зависимости от начальных условий, можно его ликвидировать. Поэтому без потери общности можно положить .

Задачу о назначениях можно представить следующим образом. Пусть

Теперь задача будет формулироваться как

Заметим, что оптимальное решение задачи о назначениях не изменится, если к любой строке или столбцу матрицы стоимостей прибавить (или вычесть) постоянную величину. В самом деле, если ивычитаются изой строки иго столбца, то новые стоимости имеют вид. Отсюда получается новая целевая функция

Поскольку , то. Следовательно, минимизация исходной целевой функцииприводит к такому же решению, как минимизация. Приведённое соображение показывает, что если можно построить новуюматрицу с нулевыми элементами и эти нулевые элементы соответствуют допустимому решению, то такое решение будет оптимальным, поскольку стоимость не может быть отрицательной.

Специфическая структура задачи о назначениях позволяет разработать эффективный метод её решения. Покажем, как реализуется этот метод на примере.

Презентация решения задачи о назначениях

Интерпретация симплекс-таблиц – анализ модели на чувствительность

Анализ моделей на чувствительность – это процесс, реализуемый после того, как оптимальное решение задачи получено. Исследователя вряд ли устроила бы заключительная симплекс-таблица, из которой можно было бы получить только список переменных и их значения. На самом же деле результирующая симплекс-таблица «насыщена» весьма важными данными, лишь небольшую часть которых составляют оптимальные значения переменных. Из симплекс-таблицы либо непосредственно, либо при помощи простых дополнительных вычислений можно получить информацию относительно

1) оптимального решения,

2) статуса ресурсов,

3) ценности каждого ресурса,

4) чувствительности оптимального решения к изменению запасов ресурсов, вариациям коэффициентов целевой функции и интенсивности потребления ресурсов.

Сведения, относящиеся к первым трем пунктам, можно получить непосредственно из симплекс-таблицы для оптимального решения. Получение информации, относящиеся к четвертому пункту, требует дополнительных вычислений.

Для иллюстрации возможностей получения указанной выше информации из заключительной симплекс-таблицы воспользуемся опять задачей 1. Эта задача формулируется следующим образом:

max ( прибыль )

Оптимальная симплекс-таблица имеет вид:

Базис	с		3		2	0		0	0		0
	2		0		1			-	0		0
	3		1		0	-			0		0
	0	3	0		0	-1		1	1		0
	0		0		0	-			0		1
Решение				0	0					0		0

1) Оптимальное решение

Управляемые переменные	Оптимальные значения	Решение
	31/3	Объём производства краски для наружных работ должен быть равен 31/3 т в сутки
	11/3	Объём производства краски для внутренних работ должен быть равен 11/3 т в сутки
	122/3	Прибыль от реализации продукции равна 122/3 тыс. долл. ( в сутки )

2) Статус ресурсов

Прямая, проходящая через оптимальную точку, представляет связывающее ограничение ( на рисунке 1.1 ограничения 1 и 2 ). В противном случае соответствующее ограничение будет несвязывающим ( на рисунке 1.1 ограничения 3 и 4 ). Связывающее ограничение относится к разряду дефицитного ресурса, несвязывающее – недефицитный ресурс.

Ресурс	Остаточные переменные	Статус ресурса
Исходный продукт А	(нет в базе)	Дефицитный
Исходный продукт В	(нет в базе)	Дефицитный
Превышение объёма производства краски для внутренних работ по отношению к объёму производства краски для наружных работ		Недефицитный
Спрос на краску для внутренних работ		Недефицитный

3) Ценность ресурса

Ресурс	Статус ресурса	Ценность ресурса
Исходный продукт А	Дефицитный
Исходный продукт В	Дефицитный
Превышение объёма производства краски для внутренних работ по отношению к объёму производства краски для наружных работ	Недефицитный	0
Спрос на краску для внутренних работ	Недефицитный	0

Полученные результаты свидетельствуют о том, что дополнительные вложения в первую очередь следует направить на увеличение исходного продукта В и лишь затем – на увеличение исходного продукта А. Что касается недефицитных ресурсов, то, как и следовало ожидать, их объем увеличивать не следует.

4) Максимальное изменение запаса ресурса

Базис	с		3	2	0	0	0	0
	0		1	2	1	0	0	0
	0	8	2	1	0	1	0	0
	0	1	-1	1	0	0	1	0
	0	2	0	1	0	0	0	1
		0	-3	-2	0	0	0	0
	0		0		1		0	0
	3	4	1		0		0	0
	0	5	0		0		1	0
	0	2	0	1	0	0	0	1
		12	0	-	0		0	0
	2		0	1		-	0	0
	3		1	0	-		0	0
	0		0	0	-1	1	1	0
	0		0	0	-		0	1
			0	0			0	0

Как изменится симплекс-таблица при изменении величины запаса ресурса на ? Проще всего получить ответ на этот вопрос, если ввестив правую часть первого ограничения начальной симплекс-таблицы и затем выполнить все преобразования. Прежде всего заметим, что на каждой итерации новая правая часть каждого ограничения представляет собой сумму двух величин: постоянной и члена, линейно зависящего от. Постоянные соответствуют числам, которые были на соответствующих итерациях в правых частях ограничений симплекс-таблиц до введения. Коэффициенты приво вторых слагаемых равны коэффициентам при на той же итерации. Другими словами, при анализе влияния изменений в правых частях второго, третьего и четвертого ограничений нужно пользоваться коэффициентами при переменных , ,соответственно.

Величина должна быть ограничена таким интервалом значений, при которых выполняется условие неотрицательности правых частей ограничений, т.е.

;