Нормальное распределение

Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Заметим, что для определения нормального распределения необходимо знать параметры: . Выясним вероятностный смысл этих параметров. Найдём математическое ожидание непрерывной случайной величины

- интеграл Пуассона. Итак, математическое ожидание нормального распределения равно параметру , т.е..

Определим дисперсию, учитывая, что .

==, т.к.. Итак,. Таким образом второй параметрравен среднему квадратическому отклонению.

Вычислим вероятность попадания в заданный интервал нормальной случайной величины.

Часто требуется вычислить вероятность того, что отклонение нормально распределённой величины по абсолютной величине меньше заданного положительного числа, т.е. требуется найти вероятность осуществления неравенства.

.

. Правило трёх сигм

Преобразуем формулу , полагая . В итоге получим.

Если t=3 и, следовательно, , то, т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события практически считаются невозможными. В этом и состоит сущность правила трёх сигм:если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трёх сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведённом правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

Показательное распределение

Показательным называется распределение вероятностей непрерывной случайной величины , которое описывается плотностью

где - постоянная положительная величина.

Найдём функцию распределения показательного закона

. Итак,

Найдём математическое ожидание =;.

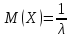Найдём дисперсию

=

=;;

Найдём вероятность попадания в интервал непрерывной случайной величины, которая распределена по показательному закону, заданному функций распределения

Функция надёжности

Всякое устройство, независимо от того, «простое» оно или «сложное» будем называть элементом.

Пусть элемент начинает работать в момент времени , а по истечении времени длительностью происходит отказ. Обозначим черезнепрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно время, меньшее, то, следовательно, за время длительностьюнаступит отказ. Таким образом функция распределенияопределяет вероятность отказа за время длительностью. Тогда вероятность безотказной работы за это же время длительностью, т.е. вероятность противоположного события, равна.

Функцией надёжности называют функцию, определяющую вероятность безотказной работы элемента за время длительностью:

.

Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого . Тогда .

Показательным законом надёжности называют функцию надёжности, определяемую равенством , где- интенсивность отказов.