Размещения с повторениями

«Опять восьмёрка!» - горестно воскликнул председатель клуба велосипедистов, взглянув на погнутое колесо своего велосипеда. «А всё почему? Да потому, что при вступлении в клуб мне выдали билет за номером 008. И теперь месяца не проходит, чтобы то на одном, то на другом колесе не появилась восьмёрка. Надо менять номер билета. А чтобы меня не обвиняли в суеверии, проведука я перерегистрацию всех членов клуба и буду выдавать только билеты с номерами, в которые ни восьмёрка, ни нуль не входят».

Сказано – сделано, и на другой день он заменил все билеты. Сколь членов было в клубе, если известно, что использованы все трёхзначные номера, не содержащие ни одной восьмёрки и ни одного нуля?

Для решения этой задачи определим сначала, сколько будет однозначных номеров. Ясно, что таких номеров будет восемь: 1 2 3 4 5 6 7 9.

А теперь найдём все двузначные номера, для чего возьмём любой из найденных однозначных номеров и припишем к нему любую из восьми цифр:

11 12 13 14 15 16 17 19

21 22 23 24 25 26 27 29

31 32 33 34 35 36 37 39

41 42 43 44 45 46 47 49

51 52 53 54 55 56 57 59

61 62 63 64 65 66 67 69

71 72 73 74 75 76 77 79

91 92 93 94 95 96 97 99

Очевидно, двузначных номеров будет . Но за каждым из них снова можно поставить любую из восьми допустимых цифр. В результате получимтрёхзначных номеров. Значит, в клубе было 512 велосипедистов.

Задача о велосипедистах относится к следующему типу задач. Даны предметы, относящиеся к различным видам. Из них составляют всевозможные расстановки попредметов в каждой, при этом в расстановки могут входить и предметы одного вида, а две расстановки считаются различными, если они отличаются друг от друга или видом входящих в них предметов, или порядком этих предметов. Надо найти общее число таких расстановок.

Расстановки описанного типа называются k- размещениями с повторениями из элементов видов и обозначается.

Естественно предположить, что если число видов равно , а в каждое размещение входитэлементов, то можно составить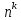размещений с повторениями. Итак,

Перестановки с повторениями

Переставляя буквы слова «ток», получим 6 различных перестановок:

ток тко отк окт кто кот

А если вместо слова «ток» взять слово «тот», то во всех выписанных перестановках надо будет заменить «к» на «т»

тот тто отт отт тто тот

При этом некоторые из наших перестановок окажутся одинаковыми и в итоге мы получим всего 3 различных перестановок.

Общая задача формулируется следующим образом: имеются предметы различных типов.Сколько перестановок можно сделать из элементов первого типа,элементов второго типа, . . . ,элементов-го типа?

Число элементов в каждой перестановке равно . Поэтому если бы все элементы были различны, то число перестановок равнялось бы!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В самом деле, возьмём, например, перестановку

в которой сначала выписаны все элементы первого типа, потом второго, . . . , наконец, 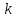-го типа. Элементы первого типа можно переставлять друг с другом! способами. Но так как все эти элементы одинаковы, то такие перестановки ничего не меняют. Точно так же ничего не меняют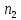! перестановок элементов второго типа и т.д. Поэтому множество всех! перестановок распадается на части, состоящие из!! . . .! одинаковых перестановок каждая. Значит, число различных перестановок с повторениями, которые можно сделать из данных элементов, равно

(

Сочетания с повторениями

Рассмотрим задачу. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоёные. Сколькими способами можно купить 7 пирожных?

Эта задача не является задачей на размещения с повторениями, так как порядок, в котором укладывают пирожные в коробку, несуществен. Задача ближе к задачам на сочетания. Но она отличается тем, что в комбинации могут входить повторяющиеся элементы, например, можно купить 7 эклеров. Такие задачи называют задачами на сочетания с повторениями.

Чтобы решить эту задачу, поступим следующим образом. Зашифруем каждую покупку с помощью нулей и единиц. Именно, сначала напишем столько единиц, сколько куплено наполеонов. Потом, чтобы отделить наполеоны от эклеров, напишем нуль, а затем – столько единиц, сколько куплено эклеров. Далее снова напишем нуль. Если не было куплено ни одного эклера, то в записи появятся два следующих друг за другом нуля. Далее напишем столько единиц, сколько куплено песочных пирожных, снова напишем нуль, и наконец, напишем столько единиц, сколько куплено слоёных пирожных. Например, если куплено 3 наполеона, 1 эклер, 2 песочных пирожных и 1 слоёное, то получим такую запись: 1110101101. Если же куплено 2 наполеона и 5 песочных, то получится запись: 1100111110.

Таким образом, число различных покупок равно числу перестановок с повторениями, которые можно составить из 7 единиц и 3 нулей. В результате получим:

.

Общая формулировка таких задач такова: имеются предметы различных типов.Сколько -комбинаций можно сделать из них, если не принимать во внимание порядок элементов в комбинации?

Эта задача в общем виде решается точно так же, как и задача и пирожных. Именно, надо зашифровать каждую комбинацию с помощью нулей и единиц: для каждого типа написать столько единиц, сколько предметов этого типа входит в комбинацию, а различные типы отделять друг от друга нулями, при этом ели предметы какого-нибудь типа совсем не вошли в комбинацию, то надо писать подряд два или большее число нулей. При этом мы получим столько единиц, сколько предметов входит в комбинацию, т.е. , а число нулей будет на 1 меньше, чем число типов предметов, т.е.. Таким образом, мы получим перестановки с повторениями изединиц инулей.

Число сочетаний с повторениями из элементов типов обозначаетсяи равно числу перестановок с повторениями изнулей иединиц. Таким образом:

.

Заметим, что .