Неоднородные линейные уравнения второго порядка с постоянными коэффициентами

Неоднородные линейные уравнения второго порядка с постоянными коэффициентами имеют вид:

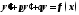, (1)

где и- действительные числа.

В предыдущей теме мы ознакомились с общим методом нахождения решения неоднородного уравнения. В случае уравнения с постоянными коэффициентами частное решение иногда бывает возможно найти проще, не прибегая к методу вариации произвольных постоянных. Рассмотрим несколько таких возможностей для данного уравнения (1).

1. Правая часть уравнения (1) представляет собой произведение показательной функции на многочлен ой степени, т.е.

(2)

Возможны следующие случаи:

1. Число не является корнем характеристического уравнения

В этом случае частное решение следует искать в виде

(3)

Найдём производные до второго порядка и подставим в уравнение (1):

или

(4)

многочлен степени 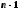, многочлен степени ,многочлен степени . Таким образом, слева и справа от знака равенства стоят многочленыой степени. Приравнивая коэффициенты при одинаковых степенях, получим системууравнений для определения неизвестных коэффициентов.

2. Число является однократным корнем характеристического уравнения

В этом случае, т.к. корень характеристического уравнения, тои слева в равенстве (4) будет стоять многочленой степени, а справаой степени. Следовательно, ни при какихравенство (4) не было бы тождеством. Поэтому в рассматриваемом случае частное решение нужно брать в виде многочленастепени, но без свободного члена, т.к. свободный член этого многочлена исчезнет при определении производной:

(5)

3. Число являетсядвукратным корнем характеристического уравнения

Тогда в равенстве (4) кроме того, что , ещё и. Следовательно, в левой части равенства (4) остаётся многочленой степени. Для того, чтобы в результате подстановки получить многочлен степени, следует частное решение искать в виде произведения показательной функции на многочленой степени . При этом свободный член и член первой степени этого многочлена исчезнут при дифференцировании:

(6)

2. Правая часть уравнения (1) имеет вид:

, (7)

где и- многочлены от, то форма частного решения определяется так:

1. Если число не является корнем характеристического уравнения

то

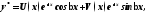(8)

где и- многочлены, степень которых равна наивысшей степени многочленови;

2. Если число является корнем характеристического уравнения

то

. (9)

_{Замечание}. Указанные формы частных решений (8) и (9) сохраняются и в том случае, когда в правой части уравнения (1) один из многочленов и тождественно равен нулю, т.е. когда правая часть имеет видили

Неоднородные линейные уравнения высших порядков

Пусть дано неоднородное линейное уравнение

(1)

где непрерывные функции отили постоянные числа. Пусть нам известно общее решение

(2)

соответствующего однородного уравнения

(3)

Для уравнения (1) справедливо утверждение: «Если общее решение однородного уравнения (3), ачастное решение неоднородного уравнения (1), тоесть общее решение неоднородного уравнения».

Как и в случае уравнения второго порядка, частное решение уравнения (1) можно находить по способу вариации произвольных постоянных, считая в выражении (2) функциями от.

(4)

В случае неоднородного уравнения высшего порядка с постоянными коэффициентами частные решения иногда находятся проще, а именно: