Системы обыкновенных дифференциальных уравнений

Рассмотрим систему уравнений первого порядка

( 1 )

гдеискомые функции,аргумент.

Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.

Решить систему – значит определить функции , удовлетворяющие системе уравнений (1) и данным начальным условиям:

( 2 )

Интегрирование системы (1) производится следующим образом.

Дифференцируем по первое из уравнений (1):

Заменяя производные их выражениямииз уравнений (1), будем иметь уравнение

.

Дифференцируя полученное уравнение и поступая аналогично предыдущему, получим:

.

Продолжая далее, таким же образом получим, наконец, уравнение

.

Итак, получим следующую систему:

( 3 )

Из первых уравнений определимвыразив их черези производные:

( 4 )

Подставляя эти выражения в последнее из уравнений (3), получим уравнение порядка для определения:

. ( 5 )

Решая уравнение (5), определим :

( 6 )

Дифференцируя выражение (6) раз, найдём производные

как функции от . Подставляя эти функции в (4), получим:

( 7 )

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Пусть дана система дифференциальных уравнений

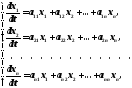( 1 )

где постоянные,аргумент,искомые функции,. Система (1) называетсясистемой линейных однородных дифференциальных уравнений с постоянными коэффициентами.

Эту систему можно решать путём сведения к одному уравнению го порядка, которое в данном случае будет линейным. Но можно решать систему (1) и другим методом, не сводя к уравнениюго порядка. Этот метод даёт возможность более наглядно анализировать характер решений.

Будем искать решение системы в виде:

( 2 )

Надо определить постоянные итак, чтобы функции удовлетворяли системе уравнений (1), т.е.

Сократив на , перенеся все члены в одну сторону и собрав коэффициенты при, получим систему уравнений

( 3 )

Выберем итакими, чтобы удовлетворялась система (3). Эта система есть система линейных однородных алгебраических уравнений относительно . Из курса линейной алгебры следует, что она будет иметь нетривиальное решение, если

( 4 )

Это уравнение называется характеристическим уравнениемдля системы (1), его корни называются корнямихарактеристического уравнения.

В качестве примера рассмотрим случай, когда корни характеристического уравнения - действительные и различные.

Для каждого корня 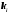напишем систему уравнений (3) и определим коэффициенты

.

Можно показать, что один из них произвольный, его можно считать равным единице. Таким образом, получаем:

для корня решение системы (1)

для корня решение системы (1)

для корня решение системы (1)

.

Путём непосредственной подстановки в уравнения можно убедиться, что система функций

( 5 )

где произвольные постоянные, тоже является решением системы дифференциальных уравнений (1). Это есть общее решение системы (1)

Р я д ы Числовые ряды Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда

Числовым рядом называется выражение вида

(5),

где члены ряда,общий член ряда (5).

Сумма первыхчленов ряда (5) называетсячастичной суммой этого ряда.

Суммой ряда называется предел частичной суммыэтого ряда при условии, чтопроизвольным способом неограниченно возрастает:

(6)

Числовой ряд, имеющий сумму в смысле этого определения, называется сходящимся, ряд же, не имеющий суммы, называется расходящимся.

Отметим некоторые свойства сходящихся рядов:

1. Если в сходящемся ряде заменить конечное число членов новыми числами, или отбросить или приписать конечное число членов ряда, или совершить перестановку любого конечного числа членов ряда, то получим новый сходящийся ряд.

2. Если все члены сходящегося ряда, сумма которого равна , умножить на некоторое число, то получится новый сходящийся ряд, сумма которого равна.

3. Сумма и разность двух сходящихся рядов есть новый сходящийся ряд. Его сумма равна соответственно сумме или разности сумм этих двух рядов.

Необходимый признак сходимости ряда. Теорема. Если ряд сходится, то его ый член стремится к нулю при неограниченном возрастании, т.е..

Доказательство. Пусть ряд (5) сходится, т.е. , тогда имеет место также и равенство. Вычитая почленно из первого равенства второе, получимили. Но, следовательно.

Следствие. Если , то ряд расходится.

Рассмотренный признак является только необходимым, но не является достаточным, т.е. из того, что , еще не следует, что ряд сходится, - ряд может и расходиться. Так, например, так называемыйгармонический ряд расходится, хотя . Покажем это. Пусть,, поэтому, или. 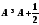Если бы гармонический ряд сходился, то по определению, а тогда последовательностьимела бы тот же предел, а в предшествующем неравенстве был бы возможен предельный переход, который привел бы к соотношению, что нелепо.