Достаточные признаки сходимости рядов с положительными членами

1. Признак сравнения. Если даны два ряда ис неотрицательными членами, причем члены первого ряда не превосходят соответствующих членов второго ряда:, то:

а) из сходимости второго ряда следует сходимость первого ряда,

б) из расходимости первого ряда следует расходимость второго ряда.

Для сравнения часто используются ряды:

1. сходящийся (геометрическая прогрессия),

2. ,

3. если иряды с положительными членами и существует конечный

,

то рассматриваемые ряды одновременно сходятся или расходятся.

Сходимость рядов вида , гдемногочлен степени,многочлен степени, полностью исчерпывается сравнением с рядом, где.

2. Признак Даламбера. Если ряд с положительными членами таков, что существуетто ряд сходится при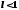и расходится при.

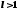Если , то вопрос о поведении ряда остается открытым.

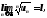3. Признак Коши. Если ряд с положительными членами таков, что существуетто ряд сходится прии расходится при.

Если 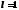, то вопрос о поведении ряда остается открытым.

4. Интегральный признак. Если функция 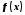непрерывная, положительная, невозрастающая дляи, начиная с некоторого,, то ряди несобственный интегралодновременно сходятся или расходятся.

Знакопеременные ряды

Из числовых рядов с произвольными знаками их членов рассмотрим прежде всего знакочередующиеся ряды.

Ряд называется знакочередующимся, если любые два соседних члена его противоположны по своим знакам.

Если считать первый член такого ряда положительным, то этот ряд запишется в виде . Сходимость знакочередующегося ряда может быть установлена признаком Лейбница:

Если члены знакочередующегося ряда убывают по абсолютной величине и , то такой ряд сходится и сумма его.

Доказательство. Рассмотрим частичную сумму четного числа членов ряда , записывая ее в двух вариантах:

1. ,

2. .

Так как по условию , то входящие в обе записи частичной суммыразности положительны; поэтому, судя по первой записи,переменная возрастающая, а по второй записи, т.е. ограничена. Из курса математического анализа следует, что возрастающая и ограниченная последовательность имеет предел, не превышающий числа.

Рассмотрим еще частичную сумму нечетного числа членов ряда 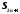в виде. Эта запись показывает, что нечетная сумма членов ряда – переменная строго убывающая., но по условию, следовательно,. Значит, последовательности частичных сумм ряда и при четном и при нечетном числе членов стремятся к одному и тому же пределу, а это доказывает сходимость заданного ряда.

В отношении знакопеременных рядов имеет место признак сходимости:

Пусть знакопеременному ряду

(7)

приводится в соответствие ряд

, (8)

составленный из абсолютных величин членов ряда (7). Тогда, если сходится ряд (8), то сходится и ряд (7).

Знакопеременный ряд (7) называется абсолютно сходящимся, если сходится ряд (8), составленный из абсолютных величин членов данного ряда. Если знакопеременный ряд (7) сходится, а составленный из абсолютных величин его членов ряд (8) расходится, то данный ряд (7) называется условно сходящимся.