Искусственное начальное решение. Метод больших штрафов.

В задаче 1 для получения начального базисного решения использовались остаточные переменные. Однако, когда исходное ограничение записано в виде равенства или имеет знак , нельзя сразу же получить допустимое начальное базисное решение. Покажем это на конкретном примере.

Начальная форма задачи: Стандартная форма задачи:

Таким образом, имеются три уравнения, содержащие четыре неизвестных. Это означает, что каждому базисному решению соответствует одна небазисная переменная (равная нулю). В отличие от случая, когда каждое уравнение содержит остаточную переменную, в данной ситуации уже нельзя быть уверенным в том, что при нулевом значении одной из переменных все базисные переменные будут неотрицательными. При выборе переменной, которой следует приписать нулевое значение, можно, конечно, использовать метод проб и ошибок. Однако этот метод требует дополнительных затрат времени и неудобен для выполнения расчетов. Поэтому следует применить более рациональный способ нахождения начального допустимого базисного решения.

Идея использования искусственных переменных достаточна проста. Она предполагает включение неотрицательных переменных в левую часть каждого из уравнений, не содержащих «очевидных» начальных базисных переменных. Обеспечивая получение начального базиса, эти дополнительно вводимые переменные выполняют, по существу, ту же роль, что и остаточные переменные. Однако, поскольку такие искусственные переменные не имеют отношения к содержанию поставленной задачи, их введение допустимо только в том случае, если соответствующая схема вычислений будет обеспечивать получение оптимального решения, в котором все искусственные переменные окажутся равными нулю.

Для построения требуемой схемы вычислений можно применить следующий прием: наложить «штраф» за использование искусственных переменных, вводимых в целевую функцию. Разработаны два метода получения стартовой точки, в которых используется «штрафование» искусственных переменных: метод больших штрафов и двухэтапный метод.

Рассмотрим схему применения метода больших штрафов в нашем примере. В первом и втором уравнениях нет переменных, выполняющих роль остаточных. Поэтому введём в каждое из этих уравнений по одной искусственной переменной, обозначив их через 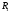и:

За использование этих переменных в составе целевой функции можно ввести штраф, приписывая им достаточно большой положительный коэффициент . Такой способ введения искусственных переменных приводит к следующей линейной модели:

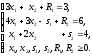
Ба- зис	сz	bi							θ	Замечания
Результи- рующая строка		zопт
Результи- рующая строка		zопт
Результи- рующая строка		zопт
Результи- рующая строка		zопт