Общие правила комбинаторики

Комбинаторные задачи бывают самых разных видов. Но большинство задач решается с помощью двух основных правил – правила суммы и правила произведения.

Правило суммы: если некоторый объект А можно выбрать способами, а другой объект В можно выбратьспособами, то выбор «либо А, либо В» можно осуществитьспособами.

При использовании правила суммы в последней формулировке надо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-нибудь способом выбора объекта В (или, как мы говорим, чтобы ни одна комбинация не попала сразу в два класса). Если такие совпадения есть, правило суммы утрачивает силу, и мы получим лишь способов выбора, где- число совпадений.

Правило произведения: если объект А можно выбрать способами и если после каждого такого выбора объект В можно выбратьспособами, то выбор пары (А,В) в указанном порядке можно осуществитьспособами.

Соединения в комбинаторике

Различные группы, составленные из каких-либо предметов и отличающиеся одна от другой или порядком этих предметов, или самими предметами, называются соединениями.

Предметы, из которых составляются соединения, называются элементами. Элементы обозначаются буквами .

Соединения могут быть трёх видов: размещения, перестановки, сочетания без повторений и с повторениями.

Рассмотрим каждый из видов в отдельности.

Размещения без повторений

Определение. Размещениями из элементов поназываются такие соединения, каждое из которых содержитэлементов, взятых из данныхэлементов, и которые отличаются одно от другого или элементами, или порядком элементов и обозначается.

Другими словами, если две выборки, отличающиеся только порядком записи символов, считают различными, то говорят о размещении из m элементов по k.

Пусть дано элементов:. Сначала составим из них все размещения по 1.

Их, очевидно, будет . Значит,.

Теперь составим все размещения по 2. Для этого к каждому из ранее составленных размещений по 1 приставим последовательно все оставшиеся элементов по 1. Так, к элементуприставим последовательно оставшиеся элементы: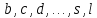; к элементуприставим последовательно оставшиеся элементы:и т.д. Получим следующие размещения по 2:

m строк

Так как всех элементов , то из каждого размещения по одному элементу мы получимразмещений по 2, а всего их будет. Значит,.

Чтобы составить размещения по 3, берём каждое из составленных сейчас размещений по 2 и приставим к нему последовательно по одному все оставшихся элементов. Тогда получим следующие размещения по 3:

m(m-1) строк

Так как число всех размещений по 2 равно m(m-1) и из каждого получается m-2 размещения по 3, то всех таких размещений окажется: m(m-1)(m-2). Таким образом . Подобно этому получим:, и вообще:

Числитель и знаменатель умножим на произведение

.

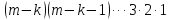
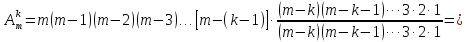
Перестановки без повторений

Если размещения из элементов взяты по(такие размещения будут различаться только порядком элементов), то такие размещения называютсяперестановками и обозначается .

Таким образом:

Сочетания без повторений

Если из всех размещений, которые можно составить из элементов по, мы отберём только те, которые одно от другого разнятся по крайней мере одним элементом, то получим соединения, которые называютсясочетаниями и обозначается .

Другими словами, если две выборки, отличающиеся только порядком записи символов, считают совпадающими, то говорят о сочетании из m элементов по k.

Например, из четырёх элементов сочетания по 3 будут:

.

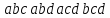Если в каждом из этих соединений сделаем всевозможные перестановки, то получим всевозможные размещения из четырёх элементов по 3:

Число таких размещений равно, очевидно, .

Таким образом, число всех размещений из 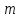элементов поравно числу всех сочетаний изэлементов по, умноженному на число всех перестановок, какие можно сделать изэлементов, т.е.. Отсюда

Формулу числа сочетаний можно привести к другому виду, если умножим числитель и знаменатель её на произведение

.

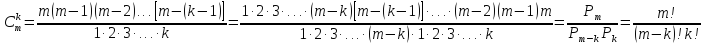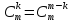Заметим, что , следовательно. Принято