
- •Министерство образования и науки Российской Федерации
- •Глава I. Наивная теория множеств
- •§ 1. Основные понятия и операции
- •Основные операции над множествами
- •Универсальные множества и операция дополнения
- •§ 2. Проверка некоторых равенств со множествами
- •§ 3. Бинарные отношения и их основные свойства
- •Способы задания бинарных отношений
- •Основные типы бинарных отношений
- •§ 4. Отношения эквивалентности и разбиения множеств
- •§ 5. Функции и их основные виды
- •Графики функций
- •Функции специального вида
- •§ 6. Композиция (суперпозиция) функций
- •Обратимые функции
- •§ 7*. Об аксиоматике Цермело-Френкеля теории множеств
- •40. Аксиома существования булеана (множества всех подмножеств) :
- •50. Аксиома (неупорядоченной) пары :
- •Глава II. Мощности множеств
- •§ 1. Счётные множества и множества мощности континуум
- •Некоторые свойства счётных множеств и множеств мощности континуума
- •§ 2. Сравнение мощностей
- •§ 3. Кардинальные числа : порядок
- •Порядок на кардиналах
- •§ 4. Кардинальные числа : арифметика
- •Основные свойства операций с кардиналами
§ 4. Отношения эквивалентности и разбиения множеств
Бинарное отношение на множестве А называется отношением эквивалентности, если оно является рефлексивным, симметричным и транзитивным.
Примеры: 1. Отношение равносильности является отношением эквивалентности на множестве Ф всех формул исчисления высказываний.
2. Отношение равенства = множеств является отношением эквивалентности на множестве B(U) – множестве всех подмножеств множества U.
3 .
Отношением эквивалентности будет
бинарное отношение подобия ~ треугольников
на множестве
всех
треугольников плоскости.
.
Отношением эквивалентности будет
бинарное отношение подобия ~ треугольников
на множестве
всех
треугольников плоскости.
4. Будет отношением эквивалентности и бинарное отношение на множестве А = {0, 1, 2, 3}, заданное графом, приведённым слева.
5. Пусть A = Z , x y (x – y 3). Проверим, будет ли отношением эквивалентности ?
Рефлексивность: a Z a – a 3 – верно, т.к. 0 3. Значит, рефлексивно.
Симметричность: a, b R a – b 3 b – a 3 – верно, т.к. если a – b 3, т.е. a – b = 3q (q Z), то b – a = 3(–q), т.е. b – a 3. Значит, симметрично.
Транзитивность: a, b, c Z a – b 3 b – c 3 a – c 3. Это тоже верно: если a – b 3 и b – c 3, то a – c = (a – b)+(b – c) 3. Таким образом, транзитивно.
Итак, – отношение эквивалентности.
Для отношения
эквивалентности
на множестве
A
с каждым элементом a
A
можно связать
множество
![]() = {b
A
| a
b},
которое называется классом
эквивалентности отношения
с представителем a.
Множество
= {b
A
| a
b},
которое называется классом
эквивалентности отношения
с представителем a.
Множество
![]() = {
= {![]() | a
A}
всех классов
эквивалентности отношения
называется
фактор-множеством
множества A
по отношению эквивалентности .
| a
A}
всех классов
эквивалентности отношения
называется
фактор-множеством
множества A
по отношению эквивалентности .
Примеры: 1. Найдём все классы эквивалентности и фактор-множество для отношения эквивалентности из предыдущего примера 4.
Ясно, что
![]() = {b
A
| 0
b}
= {0},
= {b
A
| 0
b}
= {0},
![]() = {b
A
| 1
b}
= {1, 2, 3},
= {b
A
| 1
b}
= {1, 2, 3},
![]() = {b
A
| 2
b}
= {1, 2, 3},
= {b
A
| 2
b}
= {1, 2, 3},
![]() = {b
A
| 3
b}
= {1, 2, 3}.
Таким образом, получилось всего два
различных класса эквивалентности:
= {b
A
| 3
b}
= {1, 2, 3}.
Таким образом, получилось всего два
различных класса эквивалентности:
![]() = {0}
и
= {0}
и
![]() =
=
![]() =
=
![]() = {1, 2, 3},
т.е. фактор-множество
= {1, 2, 3},
т.е. фактор-множество
![]() = {
= {![]() ,
,
![]() }
в данном
случае состоит из двух элементов. При
этом множество А
= {0, 1, 2, 3}
разбилось на два непересекающихся
подмножества: А
= {0}
{1, 2, 3}, которые
и являются найденными классами
эквивалентности:
}
в данном
случае состоит из двух элементов. При
этом множество А
= {0, 1, 2, 3}
разбилось на два непересекающихся
подмножества: А
= {0}
{1, 2, 3}, которые
и являются найденными классами
эквивалентности:
|
А |
0 |
|
1, 2, 3 |
2. Найдём все классы эквивалентности и фактор-множество для отношения эквивалентности из предыдущего примера 5.
Имеем:
![]() = {b
Z
| 0
b}
= {b
Z
| 0 – b
3} = {b
Z
| b
3} =
= {b
Z
| 0
b}
= {b
Z
| 0 – b
3} = {b
Z
| b
3} =
= {… , –6, –3, 0, 3, 6, …},
![]() = {b
Z
| 1
b}
= {b
Z
| 1 – b
3} = {b
Z
| 1 – b
= 3q
(q
Z)}
= = {b
Z
| b
= 3q
– 1} = {… , –7, –4, –1, 2, 5, 8, …},
= {b
Z
| 1
b}
= {b
Z
| 1 – b
3} = {b
Z
| 1 – b
= 3q
(q
Z)}
= = {b
Z
| b
= 3q
– 1} = {… , –7, –4, –1, 2, 5, 8, …},
![]() = {b
Z
| 2
b}
= {b
Z
| 2 – b
3} = {b
Z
| 2 – b
= 3q
(q
Z)}
= = {b
Z
| b
= 3q
– 2} = {… , –8, –5, –2, 1, 4, 7, …}.
= {b
Z
| 2
b}
= {b
Z
| 2 – b
3} = {b
Z
| 2 – b
= 3q
(q
Z)}
= = {b
Z
| b
= 3q
– 2} = {… , –8, –5, –2, 1, 4, 7, …}.
Дальнейшие попытки не дают новых множеств: например,
![]() = {b
Z
| 4
b}
= {b
Z
| 4 – b
3} = {b
Z
| 4 – b
= 3q
(q
Z)}
= = {b
Z
| b
= 3q
– 4} = {… –7, –4, –1, 2, 5, 8 …} =
= {b
Z
| 4
b}
= {b
Z
| 4 – b
3} = {b
Z
| 4 – b
= 3q
(q
Z)}
= = {b
Z
| b
= 3q
– 4} = {… –7, –4, –1, 2, 5, 8 …} =
![]() .
.
Докажем, что
полученные три класса эквивалентности
и составляют фактор-множество
![]() (т.е. что других классов уже нет). Это
легко сделать, если вспомнить, что при
делении на3
любое целое
число даёт остаток, равный либо 0,
либо 1,
либо 2.
Найденные три класса эквивалентностей
как раз и состоят из чисел, дающих при
делении на 3
остатки 0
– класс
(т.е. что других классов уже нет). Это
легко сделать, если вспомнить, что при
делении на3
любое целое
число даёт остаток, равный либо 0,
либо 1,
либо 2.
Найденные три класса эквивалентностей
как раз и состоят из чисел, дающих при
делении на 3
остатки 0
– класс
![]() ,1 –
класс
,1 –
класс
![]() и2 – класс
и2 – класс
![]() . Если взять любое числоx
Z,
то оно попадёт в один из найденных
классов, пусть, например, x
. Если взять любое числоx
Z,
то оно попадёт в один из найденных
классов, пусть, например, x
![]() (т.е. чтоx
= 2 + 3n,
n
Z)
и докажем, что
(т.е. чтоx
= 2 + 3n,
n
Z)
и докажем, что
![]() =
=
![]() .
Действительно,y
.
Действительно,y
![]()
y
{b
Z
| x
b}
= = {b
Z
| x
– b
3}
x
– y
= 3q
(q
Z)
y
= x
– 3q
= 2 + 3n
– 3q
= = 2 + 3(n
– q)
(y
даёт остаток 2 при делении на 3)
y
y
{b
Z
| x
b}
= = {b
Z
| x
– b
3}
x
– y
= 3q
(q
Z)
y
= x
– 3q
= 2 + 3n
– 3q
= = 2 + 3(n
– q)
(y
даёт остаток 2 при делении на 3)
y
![]() .
.
Итак,
![]() = {
= {
![]() ,
,
![]() ,
,
![]() },
и само множество всех целых чисел Z
разбивается
на три непересекающиеся части, являющиеся
найденными классами эквивалентности:
},
и само множество всех целых чисел Z
разбивается
на три непересекающиеся части, являющиеся
найденными классами эквивалентности:
|
Z |
… , –6, –3, 0, 3, 6, … |
|
… , –8, –5, –2, 1, 4, 7, … | |
|
… , –7, –4, –1, 2, 5, 8, … |
Сделанные наблюдения можно обобщить:
Лемма (о классах эквивалентности). Пусть – отношение эквивалентности на множестве А. Тогда
a A
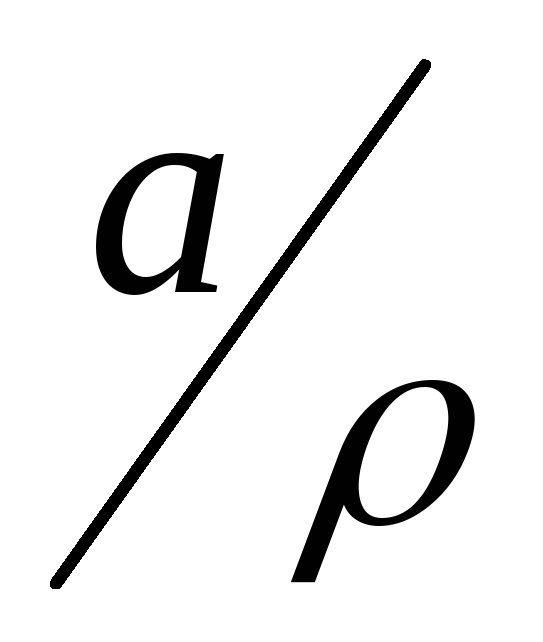
,
, a, b A (
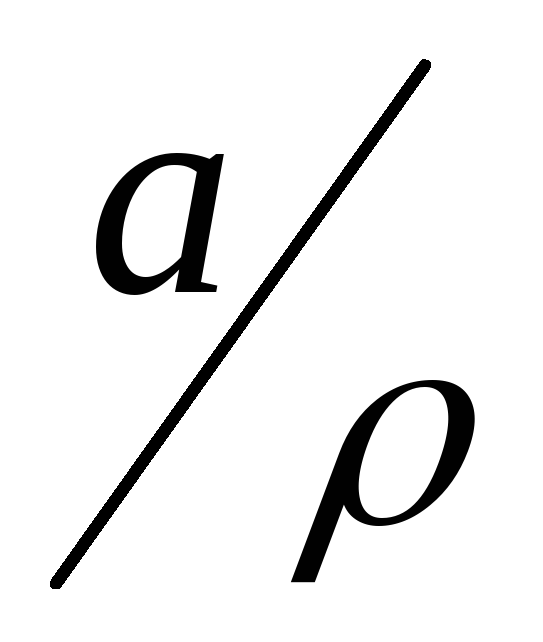 =
=
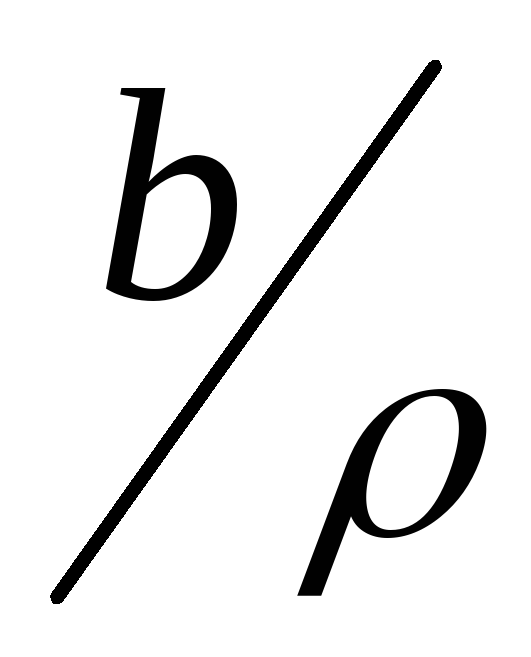 )
a
b,
)
a
b, a, b A (
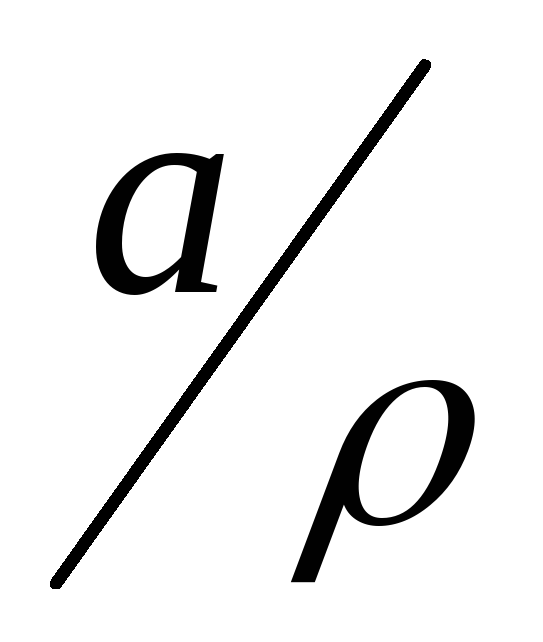
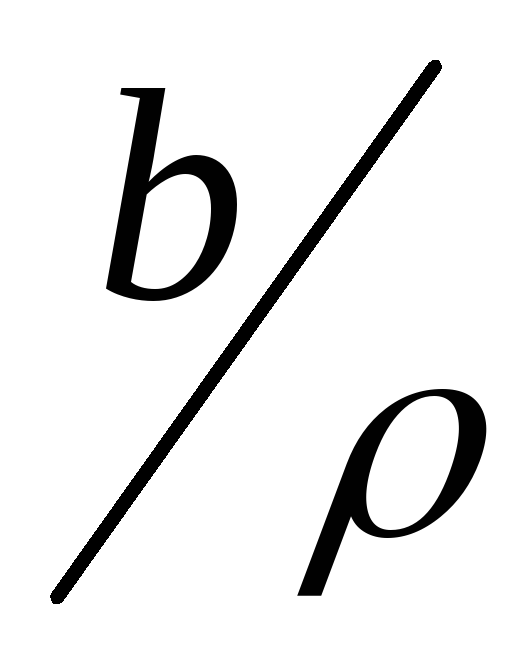 )
(
)
(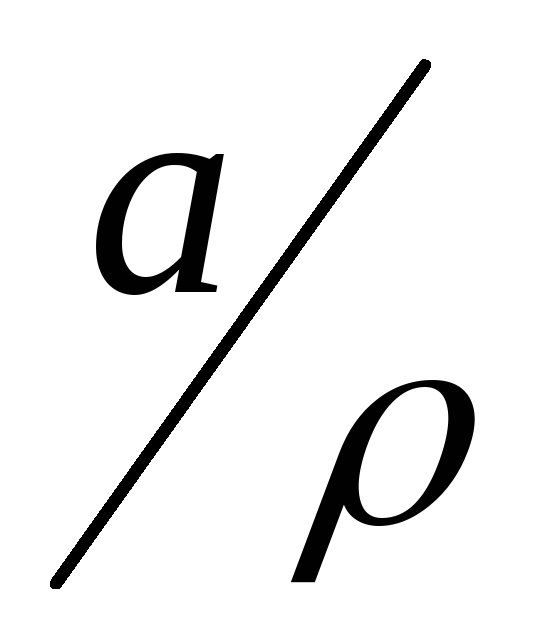
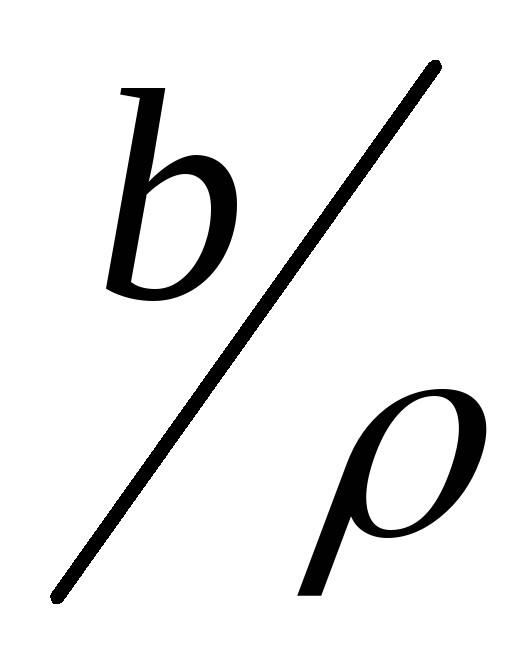 =
)
,
=
)
, a A b A a
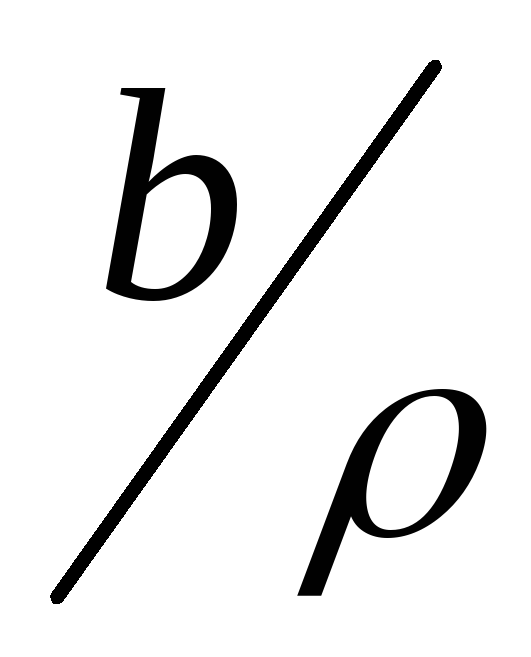 ,
т.е.
A
=
{
,
т.е.
A
=
{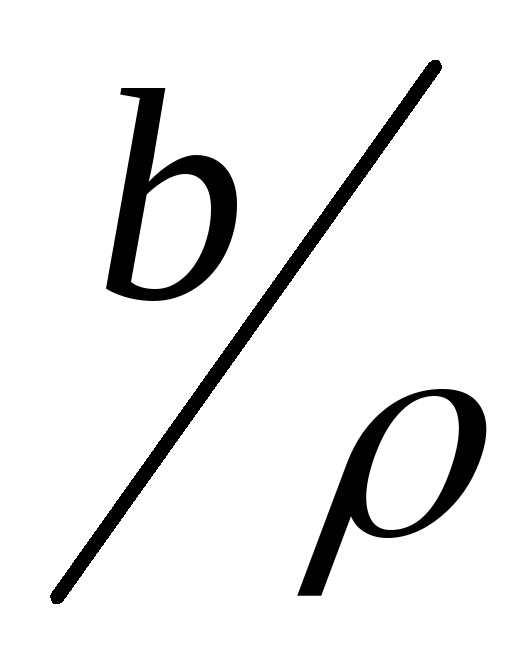 | b
A}.
| b
A}.
Доказательство.
(1)
По свойству рефлексивности отношения
эквивалентности
имеем
a
A
a
a,
т.е. a
{b
A
| a
b}
=
![]() ,
т.е.
,
т.е.![]()
.
.
(2) ()
Если
![]() =
=
![]() , тоb
, тоb
![]() =
=
![]() = {b
A
| a
b},
так что a
b.
= {b
A
| a
b},
так что a
b.
()
Предположим,
что a
b
и докажем
равенство
![]() =
=
![]() , проверив два включения
, проверив два включения![]()
![]() и
и![]()
![]() .
.
Если x
![]() = {y
A
| a
y},
то a
x,
и учитывая, что a
b,
получим a
x
a
b
{симметричность }
x
a
a
b,
откуда по транзитивности отношения
заключаем
x
b
b
x,
т.е. x
= {y
A
| a
y},
то a
x,
и учитывая, что a
b,
получим a
x
a
b
{симметричность }
x
a
a
b,
откуда по транзитивности отношения
заключаем
x
b
b
x,
т.е. x
![]() = {z
A
| b
z}.
Таким образом,
= {z
A
| b
z}.
Таким образом,
![]()
![]() .
.
Если x
![]() = {z
A
| b
z},
то b
x,
и учитывая, что a
b,
получим a
b
b
x,
откуда по транзитивности отношения
заключаем
a
x
, т.е.
= {z
A
| b
z},
то b
x,
и учитывая, что a
b,
получим a
b
b
x,
откуда по транзитивности отношения
заключаем
a
x
, т.е.
x
![]() = {y
A
| a
x},
т.е.
= {y
A
| a
x},
т.е.
![]()
![]() .
.
(3) ()
Если
![]() , нос
, нос
![]() , то a
c
b
c
a
c
c
b,
откуда по транзитивности, a
b
и (ввиду
(2))
, то a
c
b
c
a
c
c
b,
откуда по транзитивности, a
b
и (ввиду
(2))
![]() =
=
![]() – противоречие.
– противоречие.
()
Если
![]() = ,
то
= ,
то
![]() , ибо
, ибо
![]()
– противоречие.
– противоречие.
(4) Если
a
A,
то a
![]() ,
так что можно взятьb
= a.
,
так что можно взятьb
= a.
Лемма доказана.
Таким образом,
фактор-множество
![]() состоит из непустых подмножеств
множестваА
(классов
эквивалентности
состоит из непустых подмножеств
множестваА
(классов
эквивалентности
![]() ),
различные из которых не пересекаются,
а в совокупности покрывают всё множествоА (A
=
{
),
различные из которых не пересекаются,
а в совокупности покрывают всё множествоА (A
=
{![]() |a
A}),
т.е.
|a
A}),
т.е.
![]() является разбиением множестваА
в смысле
следующего определения.
является разбиением множестваА
в смысле
следующего определения.
Пусть А – непустое множество. Разбиением множества А называется любое множество X его подмножеств (X B(A)), удовлетворяющее следующим трём условиям:
(Р1): x X x (разбиение состоит из непустых множеств),
(Р2): x, y X (x = y) (x y = ) (различные элементы разбиения не пересекаются),
(Р3): A = X, т.е. a A x X a x (разбиение покрывает всё множество А).
Теорема (о разбиении на классы эквивалентности). Пусть А – непустое множество. Тогда
(1) всякое отношение
эквивалентности
на А определяет разбиение
![]() множества А на классы эквивалентности,
множества А на классы эквивалентности,
(2) Если X
– разбиение множества А, то существует
такое отношение эквивалентности
на А, что X
=
![]() .
.
Доказательство. (1) уже доказано в лемме о классах эквивалентности.
(2) Пусть задано разбиение X множества А. Определим на А бинарное отношение следующим образом: ab x X a x b x (a, b A) и проверим, что – искомое отношение эквивалентности.
Во-первых, – действительно отношение эквивалентности:
Рефлексивность: ( a A a a) ( a A x X a x a x) ( a A x X a x) – истинно ввиду (Р3).
Симметричность: ( a, b A a b b a) ( a, b A ( x X a x b x) ( x X b x a x)) – очевидно выполнено.
Транзитивность: ( a, b, c A a b b c a c) ( a, b, c A ( x X a x b x) ( y X b y c y) ( z X a z c z). Поскольку b x y, то x y и по свойству (Р2), x = y. Таким образом, a x, b x, c x и можно взять z = x X .
Итак, – отношение эквивалентности, удовлетворяющее условию b A ! x X b x (доказано при обосновании транзитивности). В дальнейшем однозначно определённый элемент x X со свойством b x будем обозначать через x(b). Тогда определение бинарного отношения можно записать в виде a b x(a) = x(b) (a, b A).
Проверим, что X
=
![]() . Действительно, еслиx
X
, то по
свойству (Р1)
существует
a
x.
Поэтому
x
= {b
A | b
x} = {b
A | a
x
b
x} = = {b
A | x(a) = x(b)} =
. Действительно, еслиx
X
, то по
свойству (Р1)
существует
a
x.
Поэтому
x
= {b
A | b
x} = {b
A | a
x
b
x} = = {b
A | x(a) = x(b)} =
![]() .
Таким
образом, X
.
Таким
образом, X
![]() .
Обратно,
если
a
A,
то
.
Обратно,
если
a
A,
то
![]() = {b
A | a
b} = {b
A | x(a) = x(b)} = x(a)
X
,
т.е.
X
= {b
A | a
b} = {b
A | x(a) = x(b)} = x(a)
X
,
т.е.
X
![]() .
.
Теорема доказана.
Примеры: 1.
Задать на множестве A
= {0, 1, 3, 5} отношение
эквивалентности с фактор-множеством
![]() = {{1}, {3}, {0, 5}}.
= {{1}, {3}, {0, 5}}.
Во-первых, ясно, что задано разбиение множества A:
|
А |
1 |
|
3 | |
|
0, 5 |
Исходя из построения отношения эквивалентности при доказательстве теоремы, можно выписать определение искомого отношения : a b x X a x b x. Более конкретно для каждого элемента:
0 b x X 0 x b x b x = {0, 5},
1 b x X 1 x b x b x = {1},
3 b x X 3 x b x b x = {3},
5 b x X 5 x b x b x = {0, 5}.
Можно нарисовать граф полученного отношения эквивалентности:
2 .
Пусть задано разбиение множества Z
на два
подмножества: чётных и нечётных чисел.
Задать соответствующее отношение
эквивалентности на множестве Z.
.
Пусть задано разбиение множества Z
на два
подмножества: чётных и нечётных чисел.
Задать соответствующее отношение
эквивалентности на множестве Z.
Понятно, что задано действительно разбиение множества Z:
|
Z |
… , –5, –3, –1, 1, 3, 5, … |
|
… , –4, –2, 0, 2, 4, … |
В соответствии с общими рассуждениями искомое отношение эквивалентности должно объявить эквивалентными между собой все нечётные числа (из первого множества разбиения) и эквивалентными между собой все чётные числа (из второго множества разбиения). Задать такое отношение можно многими способами. Например, a b a – b 2 (a, b Z) – один из возможных способов (проверьте !!).
