§ 4. Кардинальные числа : арифметика

Прежде всего, заметим, что если A, B  U, то можно найти такие множества A, B  U, что A ~ A, B ~ B, A  B = . Действительно, достаточно положить A = {u₁}A, B = {u₂}B , где u₁ , u₂  U, u₁  u₂ . Ясно, что соответствия a  (u₁ ; a) (a  A) и b  (u₁ ; b) (b  B) между множествами A и A , B и B биективны и A  B =  (?!).

Сумма + : Пусть  = , =  Card(U). Тогда их суммой называется кардинал  = .

Это определение не зависит от конкретных представителей A и B: если  = , = , то С ~ A, D ~ B, так что C ~ A, D ~ B и C  D ~ A  B. Поэтому = = .

Аналогично можно определить и суммыобщего вида: если есть множество кардиналов {_i = | i  I }, то по множествам A_i построим непересекающиеся попарно множества A_i = {{i}}A_i  U (?!) и суммой назовём кардинал, который тоже не зависит от представителейA_i (i  I).

Произведение  : Пусть  = , =  Card(U). Тогда их произведением  называется кардинал  = . Аналогично, в общем случае, если есть множество кардиналов {_i = | i  I }, то произведением назовём кардинал. Убедитесь, что эти определения не зависят от представителей.

Степень : Пусть  = , =  Card(U). Тогда степенью  ^ называют кардинал  ^ = , где, как обычно, A^B – множество всех отображений из B в A: A^B = {f : B  A | f – отображение}.

Основные свойства операций с кардиналами

1⁰.   ,  , ,   Сard(U)          +    + 

Пусть кардиналы  ,  , ,  соответствуют попарно непересекающимся множествам A, B, C, D. Нужно доказать, что если существуют инъекции f : A  B и  : C  D, то существует инъекция h : A  C  B  D. Зададим h(x) = . Это – инъекция, т.к. если h(x) = h(y), то x и y не могут принадлежать разным множествам (А  С = ), и значит, выполнены равенства f(x) = f(y) или (x) = (y), откуда (ввиду инъективности отображений f и ) x = y.

2⁰.   ,  , ,   Сard(U)           

Аналогично предыдущему. Пусть кардиналы  ,  , ,  соответствуют попарно непересекающимся множествам A, B, C, D. Нужно доказать, что если существуют инъекции f : A  B и  : C  D, то существует инъекция h : AC  BD. Зададим h((a; c)) = (f(a) ; (c)) . Проверьте сами, что это – инъекция.

3⁰.   ,  ,   Сard(U) ( + ) +  =  + ( + )

Нужно доказать, что для попарно непересекающихся множеств A, B, C верно |(A  B)  C| = |A  (B  C)|. Это очевидно ввиду закона ассоциативности объединения.

4⁰.   ,   Сard(U)  +  =  + 

Аналогично предыдущему.

5⁰.  0  Сard(U)    Card(U) 0 +  =  =  + 0

|  A| = |A| = |A  |.

6⁰.   ,  ,   Сard(U) () = ()

Нужно доказать, что |(AB)C| = |A(BC)|. Биекция между этими множествами естественна: ((a; b); c)  (a; (b; c)).

7⁰.   ,   Сard(U)  = 

Самостоятельно.

8⁰.  1  Сard(U)    Card(U) 1 =  = 1

|{a}A| = |A| = |A{a}|.

9⁰.   ,  ,   Сard(U) ( + ) =  + 

Нужно доказать, что |(A  B)C| = |(AC)  (BC)| для непересекающихся A, B. Это следует из (A  B)C = (AC)  (BC).

10⁰.   ,  ,   Сard(U)  ^{ + } =  ^ ^

Нужно доказать, что |A^{B  C}| = |A^BA^C| для непересекающихся B и C. Биекция естественна: отображению f : B  C  A ставим в соответствие пару функций (f |_B ; f |_C)  A^BA^C, где f |_X – ограничение функции f на множество X  B  C.

11⁰.   ,  ,   Сard(U) ()^ =  ^ ^

Равенство |(AB)^C| = |A^CB^C| проверяется построением биекции, ставящей в соответствие функции f : C  AB пару функций (f_A ; f_B), где f_A = π_Af, f_B = π_Bf (π_A и π_B – естественные проекции множества AB на сомножители).

12⁰.   ,   Сard(U) ( ^)^ = ^()

Равенство |(A^B)^C| = |A^BC| проверяется построением биекции, ставящей в соответствие отображению f : C  A^B отображение g : BC  A где g((b; c)) = f(c)(b)  A (нужно помнить, что f(c)  A^B является отображением из B в А).

13⁰. 1 + 1 + … = , k₁ + k₂ + … = 

|{a₁}  {a₂}  …| = |{a₁ , a₂ , …}| = |N| при попарно различных a_i (i  N),

|{1, … , k₁}  {k₁ + 1, … , k₁ + k₂ + 2}  …| = |N|.

14⁰.  +  + … = 

Объединение счётного числа счётных множеств счётно.

15⁰. n =  =  ⁿ

Декартово произведение конечного числа счётных множеств счётно, а значит, n = . Кроме того,  ⁿ = = ² ^n–2 =  ^n–2 =  ^n–1 = … = .

16⁰. 1+  +  ² + … +  ⁿ + … = 

Объединение счётного числа счётных множеств счётно.

17⁰. n^ =  ^ = c^ = c = 2^ = с

Прежде всего, c = |[0; 1]| = |{0, c₁c₂ …  R | c_i – двоичные цифры}|. Поэтому c – мощность всех последовательностей с компонентами из двухэлементного множества цифр, т.е. c = 2^.

Далее, с = 2^  n^   ^  c ^ = (2 ^)^ = = 2 ^ = c, так что все эти мощности равны.

Наконец, c  c  c ² = c .

18⁰. 1+ с + с ² + … + с ⁿ + … = 1+ с + с + … + с + … = с = с

19⁰.   ,   Сard(U) (      )  ( = max{, })

Достаточно доказать для бесконечного кардинала  равенство  ² =  : если    , то      ² =  , и значит,  =  = max{, }.

Пусть для некоторого бесконечного кардинала  верно  ²  . Тогда во в.у.м. Card(U) можно выбрать наименьший кардинал с этим свойством, который и обозначим через . По выбору  имеем   <   ² = . Рассмотрим произвольный отрезок    <  и рассмотрим кардинал  , отвечающий множеству  \  . Тогда  +  =  и выполнены соотношения:

 ² = ( + )² =  ² + 2 +  ² =  + 2 +  ².

Если  <  , то  ² =  и 2  2 ² =  , где  = max{ , }. Таким образом, в этом случае  ² =  + 2 +  ² =  +  +  =  +  =  – противоречие. Значит,  =  >  .

Для каждого    <  есть биекция _ :    ² . На множестве упорядоченных пар ( ; _ ) введём отношение порядка  : ( ; _ )  ( ; _ ) тогда и только тогда, когда  <  и _ |_ = _ . Это отношение частичного порядка. При этом, если ( ; _ )  ( ; _ )  … – возрастающая цепочка, то у неё есть верхняя грань (u ; ), где u – объединение всех кардиналов  ,  , … этой цепочки, а  : u  u ² продолжает все функции цепочки: (x) = _(x), если x   . Такое определение не зависит от выбора  : если x   , где ( ; _) < ( ; _), то _(x) = _(x), т.к. _ |_ = _ . Проверьте, что  – биекция.

П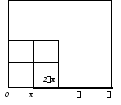о лемме Цорна существует максимальная пара(π ; ), т.е. непродолжаемое биективное отображение  : π  π ². Ясно, что  < π <  и по доказанному выше  =  – π =  > π . Рассмотрим кардинал π + π = 2π <  и распространим  до биекции  : 2π  (2π)² : квадрат (2π)² состоит из четырёх равномощных квадратиков π ² ~ π, причём π = π²   3π² = 3π  π ² = π , так что существует биекция из отрезка (π; 2π] на “уголок” из трёх квадратиков (см. рисунок выше). Таким образом,  будет по-прежнему отображать [0; π] на квадратик π ² , а отрезок (π; 2π] – на “уголок” из трёх таких квадратиков. Построенное продолжение противоречит непродолжаемости  .

20⁰.   ,   Сard(U) (      )  ( +  = max{, })

Если   , то  +    +  = 2   ² = max{, } =    + .

Итак, арифметика кардинальных чисел, с одной стороны, обобщает обычную арифметику натуральных чисел, но, с другой, привносит многие необычные черты в знакомый пейзаж.

Л И Т Е Р А Т У Р А

1. Брудно А.Л. Теория функций действительного переменного. – М.: Наука, 1971.

2. Валицкас А.И. Конспект лекций по математической логике. – Тобольск, ТГСПА им. Д.И. Менделеева, 2010.

3. Демидович Б.П. Сборник задач и упражнений по математическому анализу: Учеб. пособие. – М.: АСТ, 2002.

4. Ершов Ю.Л., Палютин Е.А. Математическая логика. – СПб.: Издательство “Лань”, 2004.

5. Игошин В.И. Математическая логика и теория алгоритмов. – М.: Издательский центр “Академия”, 2004.

6. Игошин В.И. Задачник-практикум по математической логике. – М.: Издательский центр “Академия”, 2005.

7. Ильин В.А. Математический анализ: Учебник : в 2 ч. / В.А. Ильин, В.А. Садовничий и др. - 3-е изд.,пер. и доп. - М.: Проспект, 2006.

8. Йех Т. Теория множеств и метод форсинга. – М.: Мир, 1973.

9. Кон П.М. Универсальная алгебра. – М.: Мир, 1968.

10. Кострикин А.И. Введение в алгебру (в 3-х ТТ.). – М.: ФИЗМАТЛИТ, 2000.

11. Сборник задач по алгебре / Под ред. А.И. Кострикина. – М.: ФИЗМАТЛИТ, 2001.

12. Коэн П. Дж. Теория множеств и континуум-гипотеза. – М.: Мир, 1969.

13. Кудрявцев Л.Д. Курс математического анализа. Т. I-II. – М.: Высшая школа, 1991.

14. Курош А.Г. Курс высшей алгебры. – СПб.: Издательство “Лань”, 2008.

15. Курош А.Г. Лекции по общей алгебре. – СПб.: Издательство “Лань”, 2007.

16. Лавров И.А. Математическая логика. – М.: Издательский центр “Академия”, 2008.

17. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Издательский центр “Академия”, 2007.

18. Никольский С.Н. Курс математического анализа: Учеб. для вузов. – 6-е изд. стер. – М.: Физматлит, 2002.

19. Фаддеев Д.К. Лекции по алгебре. – СПб.: Издательство “Лань”, 2002.

20. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. – СПб.: Издательство “Лань”, 2007.

21. Шварц Л. Анализ.Т. I-II. – М.: Мир, 1972.

22. Ященко И.В. Парадоксы теории множеств. – М.: Издательство МЦНМО, 2002.

*при первом чтении можно пропустить

*₀ – это буква древнееврейского алфавита, читается“алеф-ноль”.

88