Основные операции над множествами

1. Если А, В – множества, то существует множество А  В – объединение множеств А и В, которое состоит из всех элементов, являющихся элементами либо множества А, либо множества В:

x  A  B  x  A  x  B.

Примеры: 1. Если A = {1, 2, 5, }, B = {{1}, 2, 5, }, то

А  В = {1, 2, 5, , {1}}.

2. Если A = {x  R | 1 < x  5}, B = {x  R | –1  x < 2}, то

A  B = [–1; 5] = {x  R | –1  x  5}.

2. Если А, В – множества, то существует множество А  В – пересечение множеств А и В, которое состоит из всех элементов, являющихся одновременно элементами и множества А, и множества В:

x  A  B  x  A  x  B.

Примеры: 1. Если A = {1, 2, 5, }, B = {{1}, 2, 5, }, то

А  В = {2, 5, }.

2. Если A = {x  R | 1 < x  5}, B = {x  R | –1  x < 2}, то

A  B = (1; 2) = {x  R | 1 < x < 2}.

3. A  B = {a  A | a  B}.

На основе понятий пересечения и объединения двух множеств можно ввести аналогичные операции над несколькими множествами:

A₁  …  A_n = (…((A₁  A₂)  A₃)  …)  A_n ,

A₁  …  A_n = (…((A₁  A₂)  A₃)  …)  A_n .

3. Если А, В – множества, то существует множество А \ В – разность множеств А и В, которое состоит из всех элементов, принадлежащих множеству А, но не принадлежащих множеству В:

x  A \ B  x  A  x  B.

Примеры: 1. Если A = {1, 2, 5, }, B = {{1}, 2, 5, }, то А \ В = {1}.

2. Если A = (1; 5] = {x  R | 1 < x  5}, B = [–1; 2) = {x  R | –1  x < 2}, то A \ B = [2; 5].

3. A \ B = {a  A | a  B}.

4. Если А – множество, то существует множество всех его подмножеств B(A), называемое также булеаном множества А, и состоящее из всех подмножеств множества А: X  B(A)  X  A.

Важно отметить, что булеан B(A) состоит из множеств (подмножество множества А само является множеством) и содержит в качестве элементов пустое множество  и само множество А (которые в случае А =  совпадают).

Примеры: 1. Если А = , то B(A) = {}.

2. Если A = {1}, то B(А) = {, {1}}.

3. Если A = {1, 2}, то B(А) = {, {1}, {2}, {1, 2}}.

4. Если A = {1, 2, 3}, то

B(А) = {, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.

5. Можно доказать, что булеан n-элементного множества А состоит из 2ⁿ элементов. Поэтому булеан часто называют степенью множества А и обозначают 2^A.

5. Если А, В – множества, то существует их прямое (декартово) произведение АВ, состоящее из всех упорядоченных пар (a; b), где а  А, b  B:

АВ = {(a; b) | a  A  b  B}.

Примеры: 1. Если А = {1}, B = {0, 5}, то АВ = {(1; 0), (1; 5)}.

2. Если А = {0, 2}, B = {0, 5}, то АВ = {(0; 0), (0; 5), (2; 0), (2; 5)}.

3. Если множество А состоит из m элементов, а множество В – из n элементов, то можно доказать, что множество АВ состоит из mn элементов. По этой причине в названии множества АВ используется термин “произведение”. Если А = B, то множество АА состоит из m² элементов и называется декартовым квадратом множества А и обозначается через A².

Вслед за декартовым произведением двух можно ввести и декартово произведение A₁  …  A_n = ( … ((A₁  A₂)  A₃) …) A_n n множеств A₁ , … , A_n . Множество называетсядекартовой степенью множества A и обозначается A ⁿ.

Декартово произведение АВ = {(a; b) | a  A  b  B} двух множеств А и В иногда условно изображают на плоскости, трактуя компоненты упорядоченной пары (a; b) как координаты: a – координата по оси x, на которой отмечают множество А, а b – координата по оси y, на которой отмечают множество В. Таким образом, элементы (a; b)  АB условно изображаются точками на плоскости с “координатами” a и b.

О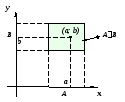собенно удобно графическое изображение декартова произведения АВ в случае, когда А и В – числовые множества, т.е. А  R, B  R . Тогда изображение принимает не условный характер, а имеет вполне конкретный геометрический смысл: множество АВ представляет из себя множество точек M(a; b) декартовой плоскости, первая координата а которых принадлежит множеству А, а вторая b – принадлежит множеству В.

Пример. Изобразим множество АВ, где A = [1; 2], B = (2; 3).

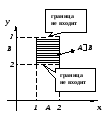
Понятие декартова (прямого произведения множеств) обобщается на случай произвольного количества множеств-сомножителей: если A₁ , … , A_k – множества, то их прямым (или декартовым) произведением А₁ … А_k называют множество, состоящее из всех упорядоченных наборов (a₁ ; … ; а_k) длины k, где а_i  А_i (1  i  k):

А₁ …  A_k = {(a₁ ; … ; a_k ) | a₁  A₁  …  a_k  A_k }.

Для k = 3 это множество можно аналогично случаю k = 2 условно изображать в пространстве. Если множества А_i содержат n_i элементов (1  i  k), то их декартово произведение содержит n₁ … n_k элементов. В случае A₁ = … = A_k = A декартово произведение А₁ …  A_k называется k-й декартовой степенью множества А и обозначается через A^k. Это название обусловлено тем, что для n-элементного множества A декартова степень A^k содержит n^k элементов.

Упражнения: 1. Перечислите все элементы множеств A  B, A  B, A \ B, B(A), AB для A = {, 0, {1}}, B = {{}, 0, 1}.

2. Изобразите на числовой оси следующие множества A  B, A  B, A \ B, B \ A, (A  B) \ (B  A), B \ (A  B) для

а) А = (1; 3], B = [2; 3); б) А = [–1; 2)  (3; 5], B = [0; 2,5]  [4; 6);

в) A = (–∞; 2), B = [–4; +∞); г) A = (–∞; 0], B = (–∞; 5).

3. Изобразите на декартовой плоскости следующие множества:

[–1; 1](0; 3], {–1; 1}(0; 3], [–1; 1]{0; 3}, {–1; 1}{0; 3}.

4. Что можно сказать о множествах А и В, если

а) А В = А  В, б) А \ В = В \ А , в) АВ = ВА, г) АВ =  ,

д) А \ (B  A) = A \ B , е) A(A  B) = (A  B)B ?