§ 2. Сравнение мощностей

В этом параграфе более формально докажем те свойства равномощности и сравнения мощностей, которыми на интуитивном уровне пользовались уже ранее.

1⁰. Любое множество равномощно самому себе:  X |X| = |X| (рефлексивность).

Это очевидно, т.к. для любого множества X биективно тождественное отображение _X : X  X, заданное правилом  x  X _X(x) = x .

2⁰. Если X равномощно Y, то Y равномощно X:

 X, Y |X| = |Y|  |Y| = |X| (симметричность).

Действительно, если f : X  Y – биективное отображение, то для него существует обратное g = f ^–1 : Y  X , которое тоже биективно.

3⁰. Если X равномощно Y, а Y равномощно Z, то X равномощно Z:

 X, Y, Z |X| = |Y|  |Y| = |Z|  |X| = |Z | (транзитивность).

Это следует из того, что если f : X  Y и g : Y  Z – взаимно однозначны, то биективна и их композиция (суперпозиция) g f : X  Z, заданная правилом  x  X g  f(x) = g(f(x)).

Таким образом, доказано, что отношение равномощности множеств обладает свойствами рефлексивности, симметричности и транзитивности, т.е. оно аналогично отношению равенства. Это отношение не является отношением эквивалентности, т.к. невозможно указать множество, на котором оно задано (множество всех множеств множеством не является). С другой стороны, если задано множество U, то это отношение равномощности будет отношением эквивалентности на множестве B(U).

Напомним, что мощность множества X меньше или равна мощности множества Y, если существует инъективное отображение f : X  Y. В этом случае пишут |X|  |Y|.

Точно так же, как в свойствах 1⁰ , 2⁰ доказываются следующие свойства

4⁰.  X |X|  |X| (рефлексивность).

5⁰.  X, Y, Z |X|  |Y|  |Y|  |Z|  |X|  |Z| (транзитивность).

Это показывает, что введённое отношение похоже на отношение порядка. Однако, для полного сходства необходимо доказать свойство антисимметричности.

6⁰.  X, Y |X|  |Y|  |Y|  |X|  |X| = |Y| (антисимметричность).

Более развёрнуто: если существуют вложения f : X  Y и g : Y  X, то существует биекция h : X  Y , т.е. |X| = |Y|.

Если одно из отображений сюръективно, то доказывать нечего, т.к. оно является и биективным. В противном случае проведём, следуя Маклейну, следующее остроумное рассуждение.

Пусть   X₁ = X \ Im(g)  X, где Im(g) = {x  X |  y  Y x = g(y)}, и если X_n  X уже определено, то X_n+1 = g  f(X_n)  X . Пусть X_∞ = X_n (см. рисунок ниже).

Тогда для любого элемента x  X_∞ верно x  X₁ = X \ Im(g), т.е. x  Im(g). Таким образом, доказано, что X \ X_∞  Im(g).

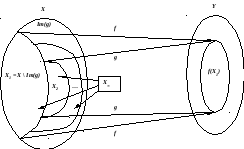
Поскольку функция g : Y  Im(g) – биективна, то существует обратная функция g ^–1: Im(g)  Y, которая, как показано выше, определена на множестве X \ X_∞  Im(g). Теперь формулой h(x) = определим функцию h : X  Y . Ясно, что h – отображение, т.е. функция h определена для любого x  X.

Это отображение инъективно. Действительно, если для x₁  x₂  X верно h(x₁) = h(x₂), то (ввиду инъективности функций f и g ^–1 ) не могут одновременно выполняться включения x₁ , x₂  X_∞ или x₁ , x₂  X \ X_∞ . Поэтому можно считать x₁  X_∞ , а x₂  X_∞ . Таким образом, f(x₁) = h(x₁) = h(x₂) = g ^–1(x₂), т.е. x₂ = g(f(x₁)) = gf(x₁). Поскольку x₁  X_k для некоторого k  N, то получается x₂ = gf(x₁)  gf(X_k) = X_k+1  X_∞ , т.е. x₂  X_∞ – противоречие.

Наконец, h сюръективно. В самом деле, если y  Y, то возможны два случая: либо g(y)  X_∞ , либо g(y)  X_∞ . В первом случае y = g ^–1(g(y)) = = h(g(y))  Im(h). Во втором случае g(y)  X_k для некоторого k  N. При этом k > 1, т.к. g(y)  Im(g). Значит g(y)  X_k = gf(X_k–1), и g(y) = gf(x_k–1) для некоторого x_k–1  X_k–1 , откуда (учитывая инъективность функции g) получим y = f(x_k–1) = h(x_k–1)  Im(h).

Итак, h – биективное отображение множества X на множество Y, что и требовалось.

Аналог антисимметричности для сравнения мощностей доказан.

Теперь докажем свойство линейности полученного порядка мощностей.

7⁰. Для любых множеств X и Y верно одно и только одно из трёх: либо |X| < |Y| , либо |X| = |Y| , либо |X| > |Y|.

Ясно, что пустое множество  содержится в любом, так что имеем || = || и || < |M| для любого непустого множества M. Поэтому в дальнейшем можно считать, что X    Y.

Допустим, что не существует вложения множества X во множество Y. Построим вложение множества Y во множество X. Для этого введём на множестве всех вложений

I = { f : B  A | A  X, B  Y, A = Im(f), f – вложение}

бинарное отношение, полагая f  g тогда и только тогда, когда функция g является продолжением функции f, т.е. f : B  A , g : D  C, B  D, A  C и  b  B f(b) = g(b). Ясно, что множество I  , т.к. в нём содержится функции f : {y}  {x} с одноэлементными областями определения и значений при любых x  X, y  Y.

Отношение  удовлетворяет, очевидно, следующим свойствам:

рефлексивности ( f : B  A f  f),

транзитивности ( f : B  A, g : D  C, h : F  E f  g  g  h  f  h),

антисимметричности ( f : B  A, g : D  C f  g  g  f  f = g).

Последнее следует из общепринятого определения равенства функций: из f  g следует B  D, A  C, а g  f означает, что D  B, C  A и  d  D f(d) = g(d). Таким образом, B = D, A = C и  d  D f(d) = g(d), т.е. f = g.

Итак,  – отношение порядка.

Кроме того, введённый порядок индуктивен, т.е. удовлетворяет следующему условию: любая возрастающая цепочка f₁  f₂  …  f_n  … имеет верхнюю грань – существует вложение f со свойством  n  N f_n  f. Действительно, если дана цепочка указанного вида, то для f_n : B_n  A_n имеют место включения B₁  B₂  … , A₁  A₂  … , а каждая функция f_n+1 является продолжением функции f_n , а значит, и всех предыдущих. Рассмотрим B = B_n , A = A_n , и построим вложение f : B  A , продолжающее все вложения цепочки. Именно, для b  B_n положим f(b) = f_n(b). Значение f(b) не зависит от номера n: если b  B_m , то f_n(b) = f_m(b), т.к. при n  m функция f_n продолжает f_m , а при m  n – f_m продолжает f_n . Функция f будет вложением, т.к. каждая функция f_n переводит разные элементы в разные. Очевидно, что f продолжает все функции цепочки, так что f – верхняя грань рассматриваемой цепи: f₁  f₂  …  f_n  …  f.

Итак, I – упорядоченное множество со свойством индуктивности. К нему можно применить лемму Цорна:

Лемма Цорна: Любое упорядоченное множество со свойством индуктивности имеет максимальный элемент.

Эта лемма, как отмечалось выше, эквивалентна аксиоме выбора. Таким образом, у множества I есть максимальный элемент, т.е. такой элемент i  I, что  f  I f  i. Докажем, что i : Y  U – вложение. Ясно, что i : V  U – вложение, т.к. i  I. Предположим, что V  Y. Тогда U  X, иначе i : V  X – биективно и существует обратное вложение i ^–1: X  V  Y вопреки первоначальному предположению. Итак, V  Y и U  X, значит можно выбрать элементы y  Y \ V, x  X \ U и продолжить вложение i до вложения j  I, где j : V  {y}  U  {x},  v  V j(v) = i(v), j(y) = x. Это противоречит максимальности вложения i, т.к. должно быть j  i, а это не так: V  {y} V.

Итак, найдено вложение i : Y  U  X, что и требовалось.

То, что никакие два условия |X| < |Y|, |X| > |Y|, |X| = |Y| не могут выполняться одновременно ясно из определений отношения < для мощностей.

Полученная теория сравнения мощностей имеет смысл, если бесконечных мощностей бесконечно много. Это действительно так, что следует из теоремы Кантора-Бернштейна:

8⁰. Теорема Кантора-Бернштейна: Любое множество не равномощноно множеству всех своих подмножеств. Более точно: если X – множество и B(X) – булеан множества X (множество всех подмножеств множества X), то существует инъекция f : X  B(X), но не существует биекции g : B(X)  X.

Функцию f : X  B(X) построить легко: можно задать f(x) = {x}  B(X).

Предположим, вопреки доказываемому, что есть биекция g : B(X)  X. Используем диагональный метод Кантора, чтобы получить противоречие. Рассмотрим множество M  X, где M = {x  X | x  g^–1(x)} . Зададимся вопросом g(M)  M ?

Если x = g(M)  M, то (по определению множества M) имеем x  g^–1(x) = = g^–1(g(M)) = M, т.е. x  M – противоречие.

Если же x = g(M)  M, то (по определению множества M) x  g^–1(x) = = g^–1(g(M)) = M, т.е. x  M – противоречие. Таким образом, g не может быть биекцией.

Теорема Кантора-Бернштейна доказана.

На самом деле, аналогичным образом можно доказать значительно больше. Пусть для множеств X, Y символ X^Y обозначает множество всех отображений из Y в X : X^Y = {f: Y  X | D(f) = Y} . В частности, если X = {0, 1}, то множество {0, 1}^Y обычно обозначают 2^Y и отождествляют с булеаном B(Y). Более точно, существует биекция : {0, 1}^Y  B(Y), которую можно задать, например, так: (f) = {y  Y | f(y) = 1}. Это действительно биекция:

инъ: если (f) = (g), то отображения f: Y  {0, 1} и g: Y  {0, 1} принимают значение 1 на одном и том же множестве, вне которого они одновременно принимают значение 0. Значит, f = g.

сюръ: для любого множества Z  B(Y), т.е. для Z  Y построим отображение f: Y  {0, 1} по правилу f(y) =. Очевидно, что (f) = Z.

Итак, можно отождествить функцию f  2^Y с множеством (f)  B(Y), т.е. отождествить 2^Y c B(Y). Кстати, для конечного множества Y из n элементов получаем равенство |2^Y| = 2ⁿ = |B(Y)| , которое и оправдывает обозначение 2^Y.

9⁰. Если X и Y – множества, причём |X| > 1, то |X^Y| > |Y| , т.е. существует вложение : Y  X^Y, но не существует биективного отображения  : Y  X^Y.

Доказательство аналогично доказательству свойства 9⁰. Зафиксируем два различных элемента x₁ и x₂ множества X.

Функцию  : Y  X^Y построить легко: например, можно задать (y) = c_y , где c_y : Y  X – задаётся правилом c_y(u) = . Отображение  инъективно: если y₁  y₂ , то , так что.

Предположим, вопреки доказываемому, что нашлась биекция  : Y  X^Y. Чтобы получить противоречие, используем диагональный метод Кантора: построим отображение f: Y  X, не содержащееся в образе отображения  .

Положим f(y) = . Тогда f(y)  (y)(y), и значит, f отлична от любой функции (y), т.е. f  Im(µ) = X^Y – противоречие.