Тетрадь 3 (функция одной переменной)
.pdf
6.14. Знайдіть найбільше й найменше значення функції f (x) x4 |
2x2 3 |
на відрізку 2;1 . |
|
Хід розв’язання. |
|
Крок 1. Знайдіть область визначення функції f (x) x4 2x2 |
3. |
D( y) : x ...
Скористайтесь тим, що степенева функція y xn |
визначена всюди при x R . |
||||||
Крок 2. |
Знайдіть похідну функції f (x) x4 |
2x2 3. |
|||||
|
4 |
2x |
2 |
|
... |
|
|
f (x) x |
|
|
3 |
|
|||
|
Для знаходження похідної |
застосуйте |
правило |
диференціювання суми |
||
|
U V та скористайтесь |
формулами: |
|
C U , де |
C const ; |
|
U V |
|
C U |
||||
xn nxn 1 .
Крок 3. Знайдіть критичні точки функції f (x) x4 2x2 3. Для цього розв’яжіть рівняння f (x) 0 .
154
|
|
4x |
3 |
4x 0 |
f (x) 0 |
|
...
x1 ... ; x2 ... ; x3 ... .
Точки, у яких похідна дорівнює нулю або її немає, називаються критичними точками.
Крок 4. Серед критичних точок функції оберіть ті, що належать відрізку 2;1 .
|
x1 ... 2;1 ; |
x2 ... 2;1 ; |
x3 ... 2;1 . |
|
||
|
Функція |
f (x) задана на відрізку 2;1 . |
|
|
||
|
Крок 5. |
Обчисліть значення функції |
f (x) у знайдених критичних |
|||
точках і точках x 2 та x 1 кінців відрізка 2;1 . |
|
|||||
|
f ( 2) ... |
|
|
|
|
|
|
f ( 1) ... |
|
|
|
|
|
|
f (0) |
... |
|
|
|
|
|
f (1) |
... |
|
|
|
|
|
Підставте у функцію f (x) |
замість змінної |
x вказані точки: x 2; |
x 1; |
||
x 0; |
x 1. |
|
|
|
|
|
Крок 6. Серед знайдених значень функції f (x) у критичних точках і на кінцях відрізка 2;1 , оберіть найбільше та найменше.
max f (x) max f ( 2); f ( 1); f (0); f (1) max ... ; ... ; ... ; ... ...
2;1
min f (x) min f ( 2); f ( 1); f (0); f (1) min ... ; ... ; ... ; ... ...
2;1
155
Якщо функція f (x) неперервна на відрізку a;b , то функція досягає свого найбільшого та найменшого значень або на кінцях відрізка a;b , або в критичних точках, які належать цьому відрізку.
|
|
|
Відповідь: M max f (x) f ( 2) 17; |
m min f (x) f ( 1) 2 . |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2;1 |
|
|
|
|
|
|
|
2;1 |
|
|
||||||||||
6.15. Знайдіть найбільше значення функції |
f (x) |
ln x |
в інтервалі |
0; . |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||||
|
|
|
Хід розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Крок 1. |
Знайдіть область визначення функції |
f (x) |
ln x |
. |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
|
D( y) : x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Скористайтесь тим, що функція y ln x визначена при x 0; . |
|
|
||||||||||||||||||||||||||||
|
|
|
Крок 2. |
Знайдіть похідну функції f (x) |
ln x |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
ln x |
|
|
|
x ... |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Для |
|
знаходження |
похідної застосуйте |
правило |
диференціювання |
частки |
||||||||||||||||||||||||
|
|
|
|
U V U V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
U |
|
|
, де U ln x, V x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Крок 3. |
|
Знайдіть критичні |
точки функції |
f (x) |
ln x |
. Для |
цього |
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
розв’яжіть рівняння f |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
(x) 0 та f |
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
f (x) |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
1 ln x 0 |
|
|
|
|
|
|
|
x 0 |
|
|
||||||||||||||||||
|
|
|
f (x) |
|
|
|
|
|
f (x) |
|
|
|||||||||||||||||||||||
...
x ... .
156
Точки, у яких похідна дорівнює нулю або її немає, називаються критичними точками.
Розв’язок логарифмічного рівняння: якщо ln x a , то x ea .
Крок 4. Серед критичних точок функції оберіть ті, що належать інтервалу 0; .
Скористайтесь тим, що функція f (x) визначна в інтервалі 0; .
Крок 5. Знайдіть другу похідну функції та визначте її значення у критичній точці x e . За знаком другої похідної у критичній точці, зробіть висновок.
|
|
|
|
|
|
|
|
|
|
|
... |
|
2 |
... |
... |
|
|
|
|
|
|
f |
|
1 ln x |
|
x |
|
|
|
... |
... |
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
4 |
||||||
(x) |
|
|
x |
|
|
|
|
x |
|
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f |
|
|
|
|
3 ln x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(x) |
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(e) ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f |
|
|
0 |
|
x |
e |
точка |
|
... |
|
|
|
|
|
|||||||
(e) ... |
|
|
|
|
|
|
|
||||||||||||||
|
Врахуйте те, |
що функція не визначена на кінцях інтервала 0; . Зважаючи |
|||||||||||||||||||
на те, є лише одна критична точка, скористайтесь другою достатньою умовою локального екстремуму.
Крок 6. Обчисліть значення f (x) у точці максимуму x e . Це і є найбільше значення функції в інтервалі 0; .
ln e
f (e) ...
e
M max f (x) f (e) ...
0;
157
Скористайтесь тим, що функція f (x) має єдину точку максимуму в інтервалі0; , тому в цій точці вона набуває найбільшого значення.
Відповідь: M max f (x) f (e) |
1 |
. |
|
||
0; |
e |
|
6.16. Визначте максимальну площу рівнобедреного трикутника, бічна сторона якого дорівнює l .
Хід розв’язання.
Крок 1. Позначте висоту трикутника x та знайдіть площу трикутника ABC , як функцію висоти x .
OC x; |
|
|
CB l |
||||||
|
|
|
|
|
|
|
|
||
OB |
... |
|
|
|
|
||||
|
|
|
|
|
|||||
AB 2OB 2 |
... |
|
|||||||
S |
|
|
1 |
OC AB |
... |
||||
ABC |
|
||||||||
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Отже, |
S (x) |
... |
|||||||
Для знаходження сторони ОВ скористайтесь теоремою Піфагора.
Формула обчислення площі трикутника: S 12 a ha , де ha висота, проведена до сторони a .
Отже, задачу можна сформулювати так: знайдіть найбільше значення функції S(x) x 
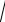l2 x2 в інтервалі 0;l .
Крок 2. Знайдіть похідну функції S(x) x 
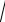l2 x2 .
|
|
|
|
|
|
|
x ... |
|
|
|
S (x) x |
l |
x |
|
... |
l |
x |
|
|
... |
158
Для знаходження похідної застосуйте правило диференціювання добутка
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
U |
|
x, V |
l |
2 |
x |
2 |
, а також формули |
|
диференціювання |
|||||||||||
U V U V U V , |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
складеної функції: U |
|
|
|
|
|
|
U . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||||||||||||||||
Крок 3. Знайдіть критичні точки функції S(x) x l2 |
x2 . Для цього |
|||||||||||||||||||||||||
розв’яжіть рівняння |
|
|
|
0 та |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
S (x) |
S (x) . |
|
|
|
|
|
|
|||||||||||||||||||
|
l2 |
2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
l |
2 |
2x |
2 |
0 |
|
|
|
|
|
|
|
l |
2 |
x |
2 |
0 |
|||||||
S (x) 0 |
|
|
|
|
|
|
|
|
S (x) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
||
|
|
|
|
|
|
x1,2 ... . |
|
|
|
|
|
|
|
x3,4 ... |
|
|
||||||||||
Точки, в яких похідна дорівнює нулю або її немає, називаються критичними точками.
Крок 4. Серед критичних точок функції оберіть ті, що належать інтервалу 0;l .
Скористайтесь тим, що функція |
f (x) |
визначна в інтервалі 0;l . |
||||
Крок 5. У критичній точці x |
1 |
|
|
функція S(x) набуває максимуму. |
||
|
|
|
|
|||
|
|
|||||
Дійсно, в інтервалі завдання 0;l |
2 |
|
|
|||
за змістом задачі функція S(x) додатна, |
||||||
на кінцях інтервалу дорівнює нулю (перевірте самостійно). Звідси випливає, що функція повинна набувати максимуму у внутрішній точці
інтервалу, а так як є лише одна критична точка x 12 , то саме вона й буде
точкою найбільшого значення функції. Знайдіть значення функції у точці x 12 .
159
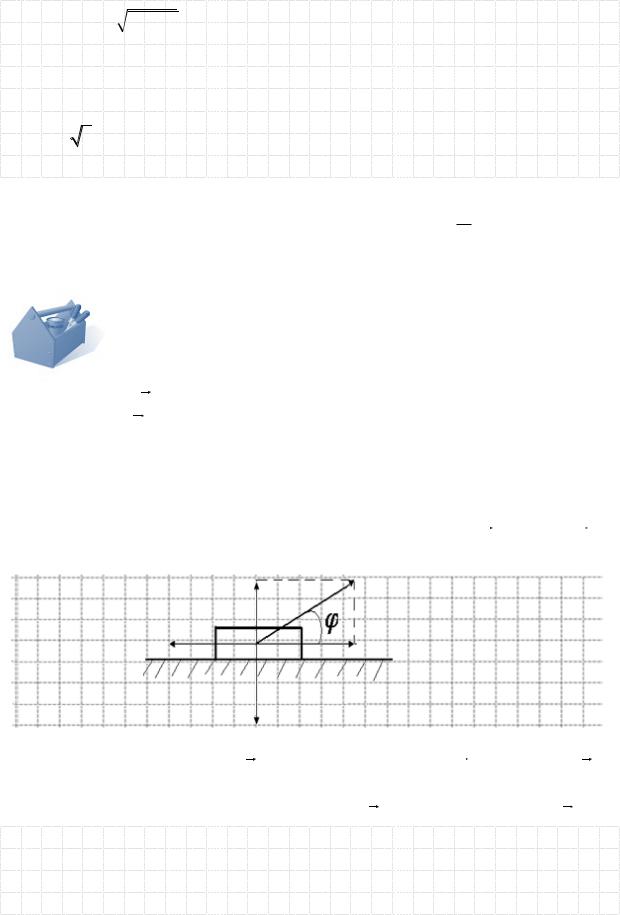
S (x) x 
l 2 x2
S (0) ...
S (l) ...
|
1 |
|
|
... |
|
S |
|
|
|
|
|
|
|
|
|||
|
|
||||
|
2 |
|
|
|
|
Відповідь: максимальна площа трикутника Smax l2 . 2
Учимося моделювати професійну діяльність інженера
6.17. Тіло вагою P , що лежить на горизонтальній площині, можна зрушити з місця силою F , що прикладена до нього. Під яким кутом до обрію необхідно прикласти цю силу, щоб її значення було найменшим?
Хід розв'язання.
Крок 1.Побудуйте схему зрушення тіла вагою P силою F з урахуванням сили тертя (позначте вказані сили на рисунку).
На тіло, крім власної ваги P і прикладеної до нього сили F , діє сила тертя R .
Крок 2. Запишіть величину сили тертя R , що діє на тіло вагою P .
Тобто R ( ... |
F sin ) |
160
Величина сили тертя пропорційна величині сили (уведіть коефіцієнт пропорційності або коефіцієнт тертя), що притискає тіло до поверхні і спрямована протилежно напряму.
Крок 3. Урівноважте величину сили тертя R на тіло, що рухається під дією сили F , прикладеної до тіла під кутом .
Отже R ... |
cos |
Враховуйте, що сила тертя R повинна врівноважуватись горизонтальною складовою F cos сили F .
Крок 4. Прирівняйте праві частини |
обох рівностей для R й |
|||
отримайте функцію залежності сили F від кута . |
||||
Одержимо (P F sin ) ... |
, |
|||
звідки F |
|
... |
|
|
|
|
|
|
|
|
... |
|
||
... |
|
|||
Застосовуйте перетворення для дробово-раціональних виразів.
|
|
|
F |
P |
|
Крок 5. |
Знайдіть найменше значення функції |
|
. |
||
cos sin |
|||||
Оберіть проміжок дослідження змінної . |
|
|
|
||
y ... |
. де ... ; ... |
|
|
|
|
Проаналізуйте функцію, що залежить від змінної (чим більше значення знаменника, тим менше значення дробу). Для дослідження функції уведіть позначання y f ( ) .
Крок 6. Дослідіть отриману функцію на найбільше значення на
161
заданому проміжку.
Похідна y / |
... . у / 0 , якщо |
tg ... |
або ... |
Знайдіть похідну функції і прирівняйте її до нуля.
Крок 7. Перевірте, чи буде отримане значення найбільшим та зробіть висновок.
Оскільки y // ... |
. 0 , то ... |
Знайдіть другу похідну для функції і порівняйте її з нулем. Якщо y 0 , то отримане значення є найбільшим.
Крок 8. Проаналізуйте отримане значення залежно від коефіцієнта тертя .
Оскільки arctg ,то ...
Розгляньте випадок, коли тіло пересувається по дерев'яному настилі, для якого
0,4 .
Відповідь: вигідніше прикладати силу F під кутом тертя бо при цьому її величина буде найменшою. Так, наприклад, якщо тіло пересувається дерев'яним настилом, то 0,4 й 22 .
162