5.4.Пересечение плоскостей общего положения (вторая основная позиционная задача

Алгоритм построения линии пересечения

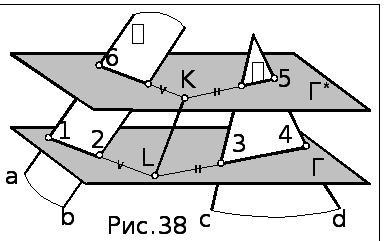Для построения линии пересечения плоскостей общего положения применяется метод вспомогательных секущих плоскостей(рис.38):

1. Проводится вспомогательная проецирующая плоскость Г, пересекающая заданные ( (а в) и  (c d)).

2. Строятся линии пересечения вспомогательной плоскости с заданными:

(12) = Г (а в), (34) = Г (c d).

3. Находится точка пересечения построенных линий пересечения: L= (12) (34). Эта точка – общая для двух заданных плоскостей и, следовательно, лежит на линии их пересечения.

4. Введя еще одну вспомогательную проецирующую плоскость Г^*, по аналогичному алгоритму находим вторую точку линии пересечения К. Если Г Г^*, то построение линии пересечения вспомогательной плоскости Г^* с заданными значительно упрощается, т.к. параллельными плоскостями плоскость пересекается по параллельным прямым.

5. Соединив одноименные проекции точек L и К, находим линию пересечения заданных плоскостей

Задача. Построить линию пересечения плоскостей общего положения  (а в) и  (c d ) (рис.38а).

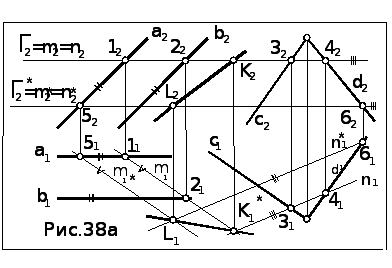Алгоритм решения

1.Проводим горизонтальную плоскость Г, пересекающую заданные плоскости.

2.Строим линии m и n пересечения вспомогательной плоскости Г с заданными плоскостями (а в) и (c d).

Фронтальные их проекции находим из условия принадлежности линий пересечения плоскости Г : m₂ = n₂ = Г₂. Горизонтальные проекции линий пересечения находим из условия их принадлежности плоскостям  (а в) и  (c d): располагаясь в  и , прямые m и n пересекают прямые, задающие эти плоскости в точках 1, 2, 3,4 соответственно. Найдя фронтальные проекции этих точек как результат пересечения одноименных проекций прямых: 1₂ = a₂m₂ , 2₂ = b₂m₂, 3₂ = с₂n₂, 4₂ = d₂n₂, горизонтальные их проекции находим по принадлежности соответствующим прямым: 1₁ a₁, 2₁  b₁, 3₁ с₁, 4₁ d₁.Соединив попарно точки 1₁,2₁ и 3₁ ,4₁ , получим горизонтальные проекции m₁ и n₁ .

3. Находим точку К – общую для заданных плоскостей: К₁ = m₁n₁ и К₂ Г₂

4. Вторую точку L искомой линии пересечения заданных плоскостей находим по аналогичному алгоритму, проведя вспомогательную плоскость Г^* Г.

5. Соединив одноименные проекции точек L и К, находим линию пересечения заданных плоскостей

5.5.Перпендикулярность прямых и плоскостей

5.5.1.Перпендикуляр к плоскости

Если плоскость – частного положения, то перпендикуляр к ней тоже прямая частного положения: перпендикуляр к проецирующей плоскости – линия уровня, к плоскости уровня – проецирующая прямая (рис.39). Проведение нормали к плоскости не требует каких-либо построений.

Если плоскость – общего положения, то перпендикуляр к ней тоже прямая общего положения и его построение основывается на следующем положении.

Определение: прямая перпендикулярна плоскости, если она перпендикулярна к каждой из двух пересекающихся прямых, лежащих в плоскости. Если пересекающиеся прямые – линии уровня плоскости, то по теореме проецирования прямого угла в горизонтальную плоскость проекций проецируется в натуральную величину прямой угол между перпендикуляром n и горизонталью, а во фронтальную - прямой угол между перпендикуляром и фронталью: n₁h₁ и n₂  f₂ .

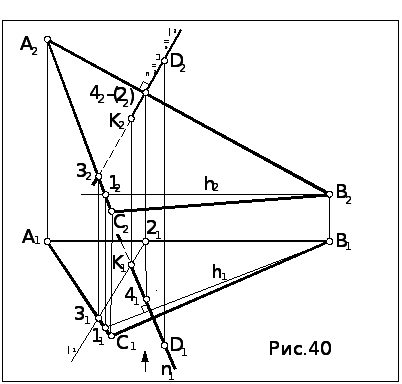
Задача. Из точки D опустить перпендикуляр на плоскость  (АВС) и найти его основание (рис.40).

Алгоритм решения

1. Проводим в плоскости  произвольные линии уровня.

Фронталь плоскости уже имеется – сторона АВ. Горизонталь h проводим через вершину В: В₂ h₂ x₂ , В₁ h₁ 1₁ .

2. Через точку D проводим нормаль к плоскости: D₁n₁.

3. Находим основание перпендикуляра (первая основная позиционная задача):

3а. Заключаем нормаль во фронтально проецирующую плоскость  : ₂ = n₂.

3б. Строим линию l пересечения плоскостей  и  (АВС): l    l₂ = ₂; l    2₁l₁3₁.

3в. Находим точку пересечения перпендикуляра n с плоскостью  (АВС): К₁ = n₁l₁ , К₂ n₂.

3г. Видимость нормали на П₂ определяем с помощью конкурирующих точек 2АС и 4n. Видимость на П₁ такая же, т.к. плоскость  - восходящая.