11.2.Пересечение поверхностей вращения второго порядка

Линия пересечения поверхностей вращения 2-го порядка в общем случае – про-странственная замкнутая кривая 4-го порядка, состоящая из двух линий в случае прони-цания или из одной - в случае врезки.

Основные точки ЛП - точки пересечения очерковых образующих одной поверх-ности с другой поверхностью и точки пересечения очерковых линий второй поверхности с первой поверхностью.

Точки ЛП в общем случае находятся способом вспомогательных секущих поверх-ностей-посредников, в роли которых могут выступать плоскости и сферы.

11.2.1.Способ секущих плоскостей (рис.82)

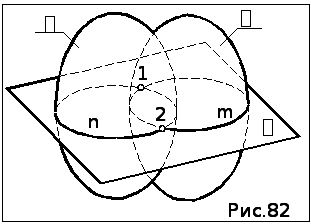1.Проводится вспомогательная плоскость , пере-секающая обе поверхности по геометрически про-стым линиям, которые проецируются также в виде геометрически простых линий (прямых или ок-ружностей).

2. Строятся линии m и n пересечения поверхно-стей  и Ф плоскостью  : m = Ф , n = .

3. Находятся точки 1 и 2 пересечения построен-ных линий пересечения m и n : 1,2 = m n.

Это и есть искомые точки ЛП заданных поверх-ностей  и Ф. Проведя достаточное число секущих плоскостей, находим достаточное количество точек ЛП.

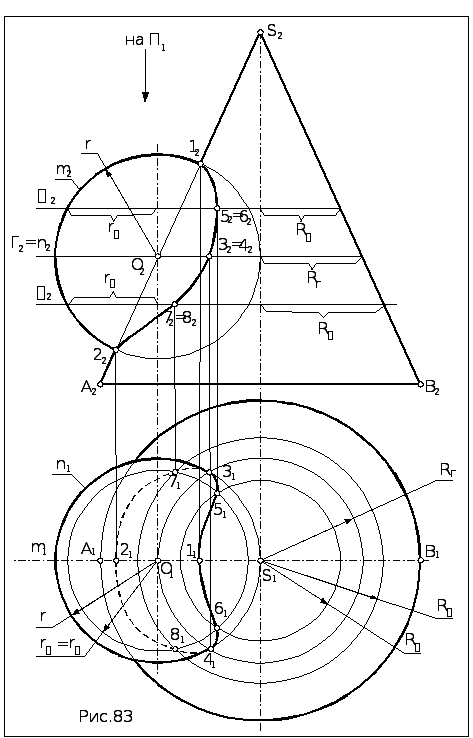
Задача. Построить линию пересечения сферы и конуса (рис.83).

Алгоритм решения

1. Определяем тип линии пересечения. Пересекаются поверхности вращения 2-го порядка, случай врезки: ЛП - одна за-мкнутая пространственная кривая 4-го порядка.

Обе поверхности имеют общую фронтальную плоскость симметрии. Следовательно, фронтальные проекции видимой и невидимой на П₂ ветвей ЛП - совпадают и замкнутая кри-вая на П₂ проецируется в виде разомкнутой.

2. Построение особых точек ЛП.

Главные меридианы сферы m и ASB конуса лежат в одной плос-кости (фронтальной плоскости симметрии) и, следовательно, пересекаются. Поэтому граничные точки видимости на П₂ находятся как результат пересечения проекций главных меридианов сферы и конуса:

1₂, 2₂ = m₂A₂S₂.. На П₁ эти точки находятся по принадлежности меридианам.

Точки пересечения горизонтального очерка сферы (экватора n) с конусом находим методом вспомогательных секущих плоскостей:

• проводим плоскость Г(Г₂) через экватор сферы,

• строим линии пересечения сферы и конуса: cфера пересекается по экватору n, который уже построен на обеих проекциях, а конус – по окружности радиуса R_Г ,

• находим проекции точек 3₁ и 4₁ пересечения этих окружностей на П₁ , а затем фронтальные проекции этих точек по принадлежности Г₂ .

3. Случайные точки ЛП находим тем же способом, что и точки 3 и 4, проводя горизонтальные секущие плоскости  и . При этом для упрощения построений проводим их на

4. Видимость ЛП и очерков поверхностей определяем по представлению.

11.2.2.Способ концентрических секущих сфер

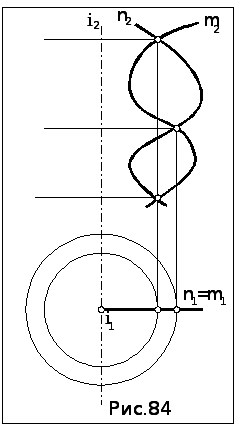
В основе способа - теорема: две соосные поверхности вращения (рис.84) пересекаются по окружностям, число которых равно числу точек пересечения главных полумеридианов m и n поверхностей. Эти окружности являются общими для обеих соосных поверхностей параллелями, плоскости которых перпендикулярны общей оси вращения.

Это обстоятельство позволяет использовать в качестве вспомогательных секущих элементов не плоскости, а сферические поверхности.

Способ секущих сфер применяется в случае,

- если решение задачи методом секущих плоскостей либо невозможно, либо графически усложнено,

- если оси заданных поверхностей пересекаются : можно провести сферу, соосную обеим поверхностям,

- если оси заданных поверхностей образуют общую плоскость симметрии, параллельную какой-либо плоскости проекций : окружности - линии пересечения сферы с поверхностями - проецируются в виде простых линий окружностей и отрезков прямых.

Алгоритм построения ЛП поверхностей способом концентрических секущих сфер аналогичен алгоритму метода секущих плоскостей:

1. Проводится сфера, соосная обеим заданным поверхностям и пересекающая их.

2. Строятся окружности - линии пересечения секущей сферы с обеими заданными поверхностями.

3. Находятся точки пересечения построенных окружностей. Это и будут искомые точки ЛП поверхностей.

Выбор параметров секущих сфер:

1.Чтобы сфера была соосна обеим заданным поверхностям, ее центр должен располагаться в точке пересечения осей вращения поверхности.

2. Радиус сферы должен удовлетворять условию Rmаx  R  Rmin.

Минимальный радиус Rmin секущей сферы определяется из условия, что сфера должна пересекать обе заданные поверхности. Сфера Rmin касается одной из поверхностей и пересекает другую, поэтому Rmin равен большей из нормалей, проведенных из центра сфер к очерковым образующим заданных поверхностей.

Максимальный радиус секущей сферы Rmax определяется из условия, что линии пересечения сферы с заданными поверхностями должны пересекаться между собой, поэтому Rmax равен расстоянию между центром сфер и наиболее удаленной от него точкой пересечения очерковых образующих заданных поверхностей.

Задача: Построить ЛП поверхностей методом концентрических секущих сфер(рис.85).

Алгоритм решения

1. Находим на П₂ точки пересечения очерковых образующих конуса SA и SB и цилиндра e и g. Судя по их горизонтальным проекциям (лежат на одной прямой, параллельной оси проекций x₁₂ ), эти образующие располагаются в одной фронтальной плоскости и пересекаются : 1₂ = S₂A₂ e₂ , 2₂ = S₂A₂g₂ , 3₂ = S₂B₂ e₂ , 4₂ = S₂B₂g₂ . Горизонтальные проекции этих точек находим по принадлежности соответствующим образующим.

2. Выбираем на фронтальной проекции параметры секущих сфер. Проекцию центра O₂ берем на пересечении осей вращения конуса i₂ и цилиндра j₂ и проводим из O₂ нормали m и n к фронтальным очерковым конуса S₂A₂ и цилиндра е₂ . Rmin равен

большей из этих нормалей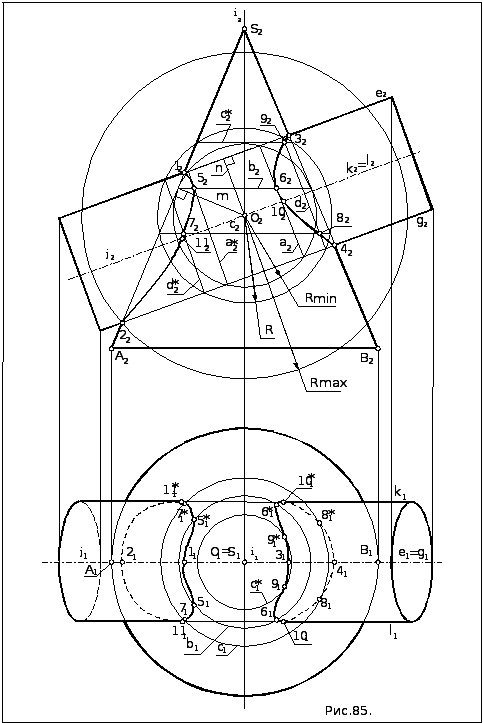: Rmin = m . Из этого, кстати, можно сделать вывод, что в месте пересечения поверхностей диаметр цилиндра меньше диаметра конуса и цилиндр полностью пересекается конусом. Значит, мы имеем дело со случаем проницания и ЛП, состоящей из двух замкнутых контуров, располагающихся на поверхности цилиндра. Rmаx принимаем равным расстоянию между центром О₂ и наиболее удаленной от него точкой 2₂ пересечения очерковых образующих поверхностей.

3. Находим на П₂ точки ЛП методом секущих сфер.

3.1. Проводим на П₂ сферу R = Rmin.

3.2. Находим точки пересечения её проекции с проекциями очерковых e₂ и g₂ цилиндра. Соединив полученные точки попарно отрезками, перпендикулярными оси j₂ цилиндра, получим проекции а₂ и а₂^* окружностей, по которым сфера пересекает цилиндр. Находим точки касания проекции сферы Rmin очерковых A₂S₂ и B₂S₂ конуса и, соединив их отрезком , перпендикулярным оси конуса, получим проекцию окружности касания сферы и конуса b₂ . Окружности а₂ , а₂^* и b₂ лежат на поверхности сферы Rmin и, следовательно, пересекаются (или параллельны как а₂ и а₂^* ).

3.3. Находим проекции точек принадлежащих искомой ЛП - точек пересечения построенных окружностей,: 5₂ =5₂^* = b₂ а₂^*, 6₂ = 6₂^*= b₂ а₂. (Для упрощения чертежа точки 5₂^* и 6₂^* условно не показаны). Горизонтальные проекции найденных на П₂ точек 5 и 6 находим по принадлежности параллели b конуса. Для этого строим на П₁ её проекцию b₁ – окружность с центром О₁ и диаметром, равным длине отрезка b₂ . Проведя сферу радиусом Rmаx  R  Rmin, по аналогичному алгоритму находим точки 7,8,9 ЛП.

4. Одноименные проекции построенных точек соединяем плавными кривыми с учетом видимости. На П₂ видимые и невидимые участки ЛП совпадают из-за наличия общей для обеих поверхностей фронтальной плоскости симметрии. Последовательность соединения точек: 1-5-7-2 для левого контура и 3-6-8-4 - для правого.

Чтобы построить горизонтальную проекцию ЛП с учетом видимости необходимо дополнительно найти граничные точки видимости на П₁ . Это точки пересечения очерковых k и l цилиндра с поверхностью конуса. Сначала находим эти точки (10₂ = 10₂^*и 11₂ =11₂^*) на П₂ как результат пересечения k₂ и l₂ с уже построенными фронтальными проекциями ЛП, а затем – 10₁ , 10₁^*,11₁ , 11₁^* по принадлежности k₁ и l₁ . Видимыми на П₁ будут участки ЛП, лежащие на верхней части цилиндра (1-5-7-11 и 3-9-6-10), невидимыми – лежащие на нижней его части.

5. Определяем видимость очерков поверхностей. На П₂ видимыми будут те части очерка конуса, которые лежат вне очерка цилиндра, и те части очерка цилиндра, которые лежат вне очерка конуса. На П₁ видимыми будут те части очерковых k и l , которые расположены правее точек 10 и левее точек 11.

11.3.Особые случаи пересечения поверхностей вращения второго порядка

В общем случае поверхности вращения 2-го порядка пересекаются по пространственным кривым 4-го порядка. Существуют частные случаи, когда такие поверхности пересекаются по плоским кривым второго порядка.

С одним таким случаем - соосными поверхностями - мы познакомились выше. Другие признаки распадения кривой 4-го порядка на плоские кривые 2-го порядка сформулированы в следующих теоремах.

Теорема о двойном прикосновении: если две пересекающиеся поверхности вращения 2-го порядка имеют две точки касания, то линия их пересечения распадается на две плоские кривые 2-го порядка, плоскости которых проходят через прямую, соединяющую точки касания.

Под точкой касания поверхностей понимается такая их общая точка, через которую можно провести плоскость, касательную к обеим поверхностям.

Теорема Монжа: если две пересекающиеся поверхности 2-го порядка описаны около третьей поверхности 2-го порядка или вписаны в нее, то линия их пересечения распадается на две плоские кривые 2-го порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания поверхностей.

На рис.86 показаны два цилиндра вра-щения, описанные вокруг сферы радиуса r. По теореме Монжа они имеют две точки касания А = e l и В = f k, через которые можно провести фронтальные плоскости  (₁) и ^*(₁^*), касающиеся обеих цилиндров по образующим e, f и k, l. На П₂ проекции точек А и В, найденные по принадлежности образующим e и f, совпадают (A₂ = B₂), то есть отрезок (АВ) – фронтально проецирующий, и плоскости кривых, по которым пересекаются цилиндры, также фронтально проецирующие и проецируются на П₂ в виде отрезков, проходящих через A₂ = B₂ . Для построения этих отрезков достаточно построить еще две пары точек, принадлежащих обоим цилиндрам. Это точки пересечения фронтальных очерковых, лежащих в одной фронтальной плоскости Ф(Ф₁): 1₂ = m₂c₂ , 2₂ = m₂d₂ , 3₂ = n₂ c₂ , 4₂ = n₂ d₂ .

Cоединив попарно точки 1₂ и 4₂ , 2₂ и 3₂ отрезками, получим проекции ЛП цилиндров - двух плоских кривых второго порядка. Т.к. плоскости их наклонены к осям цилиндров, то это эллипсы. На П₁ эллипсы проецируются на окружность – вырожденную проекцию горизонтально проецирующего цилиндра.