8. Кривые линии

В начертательной геометрии кривую линию рассматривают как траекторию непрерывно движущейся точки. Кривые могут быть: плоскими и пространственными.

Кривые могут быть заданы либо алгебраической или трансцендентной функцией, либо графически.

Порядок кривых может быть определен степенью алгебраического уравнения; по числу точек пересечения кривой с прямой линией (для плоских кривых); по числу точек пересечения кривой с плоскостью (для пространственных кривых). В начертательной геометрии кривые линии задаются на чертеже их проекциями.

Чтобы определить, какая - плоская или пространственная - кривая задана на чертеже, нужно провести две секущих, одноименные проекции которых бы пересекались, и определить их взаимное положение: если они пересекаются, то кривая плоская, если скрещиваются - пространственная. На рис.64 изображена пространственная кривая, т.к. секущие АВ и CD скрещивающиеся: точки пересечения одноименных проекций не лежат на одной линии связи.

8.11.Плоские кривые. Касательные и нормали

Направление движения точки в каждом ее положении определяется касательной прямой t в данной точке А кривой линии (рис.65).

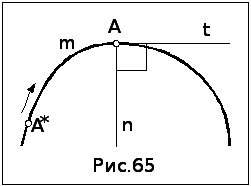Касательной прямой t в точке A кривой называется предельное положение секущей AA* , когда A* оставаясь на кривой m, стремится к точке A .

Нормалью n к кривой в точке A называется прямая, лежащая в плоскости кривой m и перпендикулярная к касательной t этой точке.

Кривая называется гладкой, если она во всех своих точках имеет непрерывно изменяющуюся касательную, которая в каждой точке кривой единственная.

На кривых различают особые точки (рис.66):

А - точка возврата 1-го рода, В - точка возврата 2-го рода, С – точка перегиба, D – кратная точка, Е – точка излома.

8.2.Основные свойства проекций плоских кривых линий

- Порядок плоской алгебраической кривой при параллельном проецировании не изменяется.

- Бесконечно удаленные точки кривой проецируются в бесконечно удален­ные точки ее проекции.

- Касательная к кривой проецируется в касательную к ее проекции.

- Точки пересечения плоских кривых проецируются в точки пересечения их проекций.

8.3.Проецирование окружности

Окружность проецируется в натуральную величину в какую-либо плоскость проекций, если она расположена в плоскости уровня, этой плоскости проекций параллельной. В прочих случаях окружность проецируется с искажением.

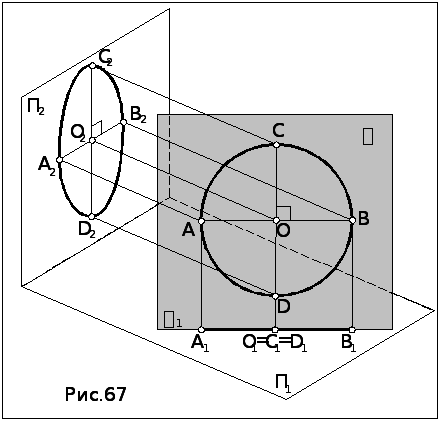
Если окружность лежит в проецирующей плоскости  (рис.67), то в плоскость проекций, перпендикулярную плоскости , окружность проецируется в виде отрезка, равного диаметру окружности (А₁В₁= АВ), на вырожденной проекции ₁.

В плоскости проекций, к которым плоскость  наклонена, окружность проецируется в виде эллипса.

При этом:

• центром эллипса О₂ является проекция центра О окружности,

• большой осью эллипса будет проекция того диаметра окружности, который параллелен плоскости проекций и проецируется в неё в натуральную величину (С₂D₂ = CD),

• малой осью эллипса будет проекция того диаметра окружности, который проецируется с наибольшим искажением в рассматриваемую плоскость проекций. На рис.66 это диаметр АВ, который лежит на линии наибольшего наклона плоскости  к П₂.

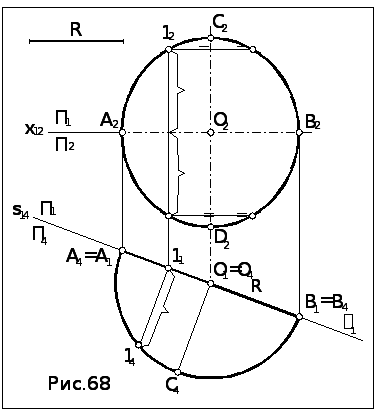Задача. Построить проекции окружности радиуса R , расположенной в горизонтально проецирующей плоскости  (рис.68).

Алгоритм решения

1. Так как плоскость  окружности горизонтально проецирующая, то в П₁ окружность проецируется в виде отрезка на вырожденной проекции ₁ плоскости, длина которого равна 2R, а на П₂ – в эллипс (см. выше рис.67), оси которого - проекции диаметров окружности: большая ось - проекция диаметра CD, который проецируется на П₂ в натуральную величину 2R (лежит на горизонтально проецирующей прямой); малая ось - проекция диаметра АВ, который проецируется с наибольшим искажением (расположен на линии наибольшего наклона к П₂, в данном случае это горизонталь, фронтальная проекция которой параллельна оси x₁₂).

2. Для построения случайных точек эллипса П₂ заменяем на П₄, располагая последнюю параллельно плоскости  окружности (на рис.68  совмещена с плоскостью окружности): П₂ П₄ , П₁ / П₂ (x₁₂) П₁ /П₄ ( s₁₄ ₁ )

В системе П₁ /П₄ нам известны обе проекции окружности и можно взять любую точку на окружности, например 1₄, а затем построить ее проекции в П₁ и П₂ по алгоритму построения проекции точек при замене плоскостей проекций (см. стр.21, рис.44). Построив 1₂, можно воспользоваться свойством симметрии эллипса и построить ещё три точки, симметричные 1₂ относительно осей А₂В₂ и C₂D₂. Соединив лекалом построенные на П₂ точки, получим эллипс – фронтальную проекцию окружности.

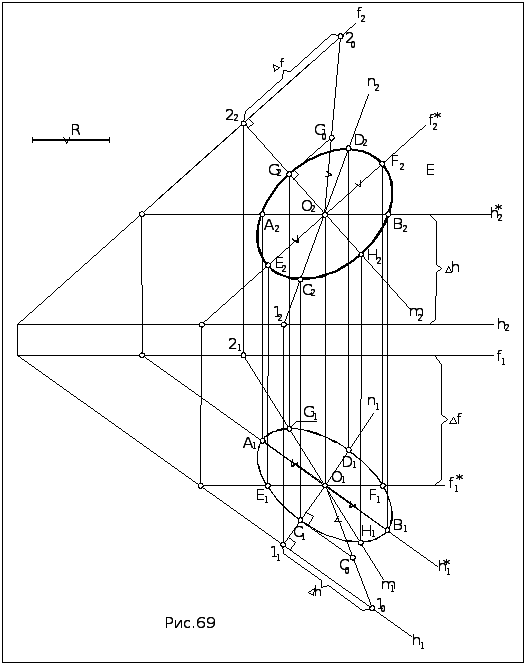
Задача. Построить проекции окружности расположенной в плоскости общего положения (рис.69).

Алгоритм решения

В обе плоскости проекции окружность проецируется в виде эллипсов. Большие оси эллипсов - это проекции диаметров окружности, лежащих на прямых уровня, а малые - проекции диаметров, лежащих на прямых наибольшего наклона плоскости окружности к соответствующей плоскости проекций.

1. Строим горизонтальную проекцию окружности. Большая ось эллипса располагается на горизонтали h*, поэтому на h₁* откладываем от проекции центра окружности О₁ величины радиуса R (помечено значком ), и получаемА₁В₁ – большую ось эллипса. Проводим линию n наибольшего наклона к П₁: О₁n₁ h₁*, О₂n₂1₂.

На прямой наибольшего наклона радиус окружности проецируется с искажением и чтобы отложить его, используем способ прямоугольного треугольника (см. стр.10, рис.14):

• определяем НВ отрезка (О1), взяв в качестве первого катета горизонтальную его проекцию (О₁1₁), а в качестве второго разность высот hего концов;

• на гипотенузе О₁1₀ (НВ отрезка (О1)) откладываем от точки О₁ радиус R () и получаем точкуС₀;

• проведя через С₀ линию, параллельную h₁ , находим на О₁1₁ точку С₁ : отрезок О₁С₁ – малая полуось эллипса; точку D₁, лежащую на другом конце малой оси, находим из условия симметрии - О₁С₁= О₁D₁.

Фронтальные проекции точек A,B,C,D находим по принадлежности прямым h₂* и n₂ соответственно.

2.Строим фронтальную проекцию окружности по аналогичному алгоритму.

3. Одноименные проекции построенных точек А,В,С,D,E,F,G,H соединяем лекалом дугами эллипса.