6.3.Вращение вокруг проецирующей прямой

При вращении вокруг оси точка описывает окружность, плоскость которой перпендикулярна оси вращения. Т.к. ось вращения - проецирующая прямая, то плоскость 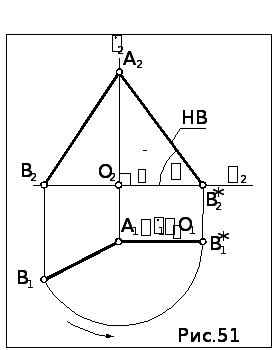окруж-ности параллельна плоскости проекций, которой перпендикулярна ось вращения. В эту плоскость проекций окружность проецируется в натуральную величину, а в другую - в виде отрезка, перпендикулярного оси вращения (рис.50).

Задача. Вращением вокруг проецирующей прямой определить НВ отрезка АВ прямой общего положения (рис.51).

Алгоритм решения

1. Выбираем в качестве оси вращения i горизонтально проецирующую прямую, проходящую через один из концов отрезка A.

2. Строим на плоскостях проекций траектории вращения другого конца отрезка: окружность R = B₁O₁ на П₁ и ₂  i₂ на П₂.

3. Строим проекции отрезка, когда он находится в положении прямой уровня: А₁В₁^*x₁₂. На П₂.в этом положении отрезок и угол  наклона к П₁ проецируются в натуральную величину.

6.4.Вращение вокруг прямой уровня

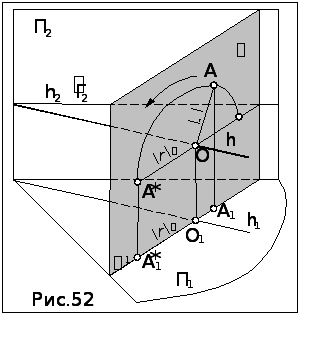
Этот способ преобразования чертежа эффективен при определении НВ плоской фигуры. В плоскости фигуры проводят прямую уровня и вращают фигуру вокруг этой прямой до положения плоскости уровня.

При вращении вокруг прямой уровня, например, горизонтали h, как это показано на рис.52, точка А описывает окружность, плоскость которой  перпендикулярна оси вращения и плоскости проекций П₁. Центр вращения O- точка пересечения плоскости вращения  с осью вращения h. Когда радиус вращения OA станет параллельным П₁, то плоскость, проходящая через точку А и ось вращения, станет горизонтальной плоскостью уровня Г.

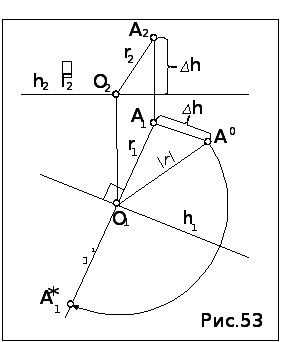Задача. Повернуть то-чку А вокруг горизонтали h до совмеще-ния с горизонтальной плос-костью Г(Г₂), проходящей через ось вращения (рис.53).

Алгоритм решения

1. Строим горизонтальную проекцию ₁ траектории вращения точки А: А₁₁  h₁ .

2. Определяем центр вращения: О₁ = ₁ h₁ , О₂ h₂

3. Строим проекции радиуса вращения и методом прямоугольного треугольника определяем его НВ.

4. Отложив от центра вращения О₁ на горизонтальной проекции ₁ траектории вращения НВ радиуса вращения, получим искомое положение точки А – А^*.

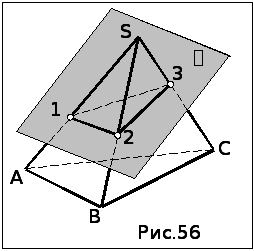
Задача. Определить натуральную величину АВС (рис.54).

Алгоритм решения

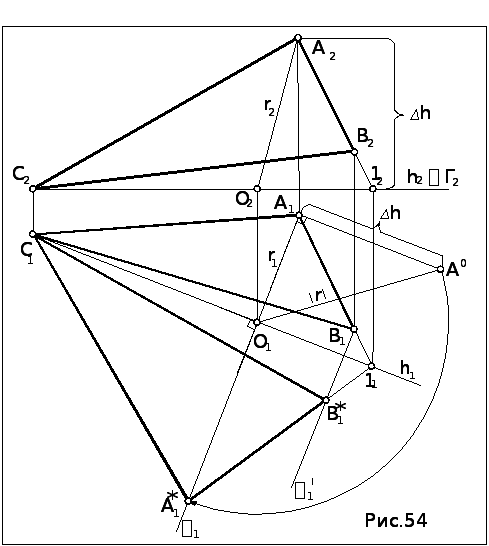
1. Выбираем в качестве оси вращения произвольную прямую уровня плоскости. Для удобства построений и во избежание наложения построений при решении в качестве оси вращения выбираем горизонталь С1, проходящую вне треугольника: С₂h₂ x₁₂ , С₁h₁ 1₁.

2. Поворачиваем вершину А вокруг оси до искомого положения (см, предыдущую задачу).

3. Достраиваем горизонтальную проекцию треугольника в положении «*», параллельном П₁. Точки С₁ и 1₁ не изменяют своего положения при вращении, а вершину В₁^* находим по принадлежности отрезку А₁^*1₁, проведя траекторию ₁^/ перемещения В₁.

А₁^*В₁^*С₁ – НВ треуголь-ника

.

7. Многогранники

На комплексном чертеже многогранники изображаются проекциями своих вершин и ребер с учетом видимости.

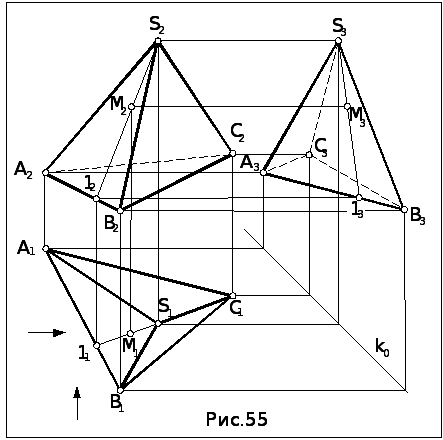
Задача. Построить проекции многогранника по заданным вершинам. Найти недостающие проекции точки М, принадлежащей поверхности многогранника (рис.55).

Алгоритм решения

1.Построив профильные проекции вершин пирамиды, соединяем одноименные проекции вершин отрезками и получаем проекции пирамиды. Видимость ребер и граней определяем по представлению. На П₁ видны боковые ребра и грани пирамиды, т.к. вершина S располагается над основанием АВС. Рассматривая горизонтальную проекцию совместно с направлением на П₂, определяем, что видимыми на П₂ являются грани ASB и BSС , а грань АSC и её ребро АС – невидимы. Аналогичным образом определяем, что на П₃ невидимыми являются ребра прилегающие к вершине С.

2. Строим недостающие проекции точки М, принадлежащей пирамиде, используя признак принадлежности точки гранной поверхности: точка принадлежит поверхности многогранника, если лежит на прямой, принадлежащей какой-либо грани этой поверхности. Точка М видима на П₂ (её проекция не заключена в скобки), следовательно, она лежит в грани ASB. Проводим в этой грани через М₂ произвольную прямую, например, S₂1₂ ,строим остальные проекции прямой и по принадлежности им находим недостающие проекции точки. Т.к. грань ASB видима на всех проекциях, то и точка М везде является видимой.