
- •Оглавление
- •1. Методы проецирования
- •1.2.Параллельное и ортогональное проецирование
- •1.3.Свойства ортогонального проецирования
- •1.4.Обратимость чертежа
- •2. Трёхкартинный чертеж точки
- •2.1.Аппарат проецирования
- •2.2.Конкурирующие точки
- •3. Чертеж прямой
- •3.1.Положение прямой относительно плоскостей проекций
- •3.1.1.Прямая общего положения.
- •3.1.2.Прямая уровня
- •3.1.3.Проецирующая прямая
- •3.2.Взаимное положение прямых
- •4. Комплексный чертеж плоскости
- •4.1.Положение плоскости относительно плоскостей проекций
- •4.1.1.Плоскость общего положения
- •4.1.2.Проецирующая плоскость
- •4.1.3.Плоскость уровня
- •4.2.Принадлежность прямой и точки плоскости
- •4.3.Прямые особого положении в плоскости
- •4.3.1.Прямая уровня плоскости
- •4.3.2.Прямая наибольшего наклона плоскости к какой-либо плоскости проекций
- •5. Взаимное положение прямой и плоскости, двух плоскостей
- •5.1.Параллельность прямой и плоскости
- •5.2.Параллельность плоскостей
- •5.3.Пересечение прямой и плоскости
- •5.3.1.Пересечение прямой и плоскости частного положения
- •5.3.2.Пересечение плоскостей, одна из которых – частного положения
- •5.4.Пересечение плоскостей общего положения (вторая основная позиционная задача
- •5.5.Перпендикулярность прямых и плоскостей
- •5.5.1.Перпендикуляр к плоскости
- •5.5.2.Плоскость, перпендикулярная прямой
- •5.5.3.Взаимно перпендикулярные прямые
- •5.5.4.Взаимно перпендикулярные плоскости
- •6. Способы преобразования чертежа
- •6.1.Замена плоскостей проекций
- •6.2.Плоскопараллельное перемещение
- •6.3.Вращение вокруг проецирующей прямой
- •6.4.Вращение вокруг прямой уровня
- •7. Многогранники
- •7.1.Пересечение многогранника плоскостью
- •7.2.Пересечение многогранника прямой
- •7.3.Взаимное пересечение многогранников
- •8. Кривые линии
- •8.11.Плоские кривые. Касательные и нормали
- •8.2.Основные свойства проекций плоских кривых линий
- •8.3.Проецирование окружности
- •8.4.Цилиндрическая винтовая линия
- •9. Криволинейные поверхности
- •9.1.Очерк поверхности
- •10. Поверхности вращения
- •10.1.Основные линии поверхности вращения.
- •10.3.Построение сечения поверхности вращения плоскостью
- •10.4.Пересечение поверхности прямой линией
- •11. Взаимное пересечение поверхностей
- •11.2.Пересечение поверхностей вращения второго порядка
- •11.2.1.Способ секущих плоскостей (рис.82)
- •11.2.2.Способ концентрических секущих сфер
- •12. Развертки поверхностей
- •12.1.Развертка призмы
- •12.2.Развертка пирамиды
- •12.3.Развертка цилиндрической поверхности
- •12.4.Развертка конической поверхности
5. Взаимное положение прямой и плоскости, двух плоскостей
5.1.Параллельность прямой и плоскости
Определение: прямая и плоскость называются параллельными, если они не имеют общей точки.
Признак: прямая параллельна плоскости, если она параллельна прямой, лежащей в плоскости.
Задача.
Через точку М
провести прямую l,
параллельную плоскости
(a![]() b)
и П1
(рис.33).
b)
и П1
(рис.33).
Алгоритм решения
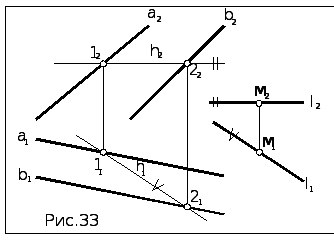 1. Т.к. искомая
прямая l
должна быть параллельна П1,
в плоскости
(a
1. Т.к. искомая
прямая l
должна быть параллельна П1,
в плоскости
(a![]() b)
проводим произвольную горизонталь h:
сначала h2
b)
проводим произвольную горизонталь h:
сначала h2![]() x12,
а затемh1по точкам 1и2:
11
x12,
а затемh1по точкам 1и2:
11![]() h1
h1![]() 21
21
2.
Через проекции точки М
проводим l2
![]() h2
и
l1
h2
и
l1![]() h1.
h1.
Задача
решена: прямая l
![]()
(a
(a![]() b),
т.к. она параллельна h,
лежащей в плоскости, и l
b),
т.к. она параллельна h,
лежащей в плоскости, и l
![]() П1,т.к.
l2
П1,т.к.
l2
![]() x12.
x12.
5.2.Параллельность плоскостей
Определение: плоскости являются параллельными, если не имеют общей точки.
Признак: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны
Задача.
Через точку М
провести плоскость ,
параллельную плоскости
(a![]() b)
(рис.34).
b)
(рис.34).
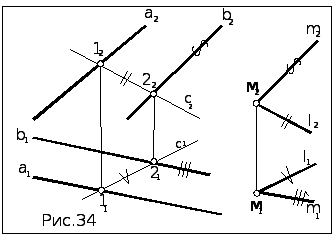 Алгоритм
решения
Алгоритм
решения
1. В
заданной плоскости нет пересекающихся
прямых, поэтому проводим в ней
дополнительную прямую с
,пересекающую
прямые, задающие плоскость
(a![]() b).
b).
2.
Искомую плоскость
задаём двумя пересекающимися прямыми
m
![]() a
и l
a
и l ![]() с, проведенными
через точку М.
с, проведенными
через точку М.
5.3.Пересечение прямой и плоскости
5.3.1.Пересечение прямой и плоскости частного положения
Задача. Построить точку К пересечения прямой l с проецирующей плоскостью (рис.35).
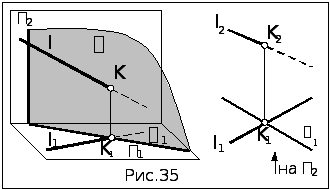 Алгоритм
решения
Алгоритм
решения
1.
Точка К
общая для прямой и плоскости. Из условия
принадлежности её плоскости
горизонтальная проекция К1
должна располагаться на вырожденной
проекции плоскости 1.
Из условия принадлежности её прямой l
проекции точки должны лежать на проекциях
прямой. Следовательно, К1
лежит
в точке пересечения 1
и
l1:
l1![]() К1
К1![]() 1
. Фронтальная
проекция К2
находится по принадлежности прямой l
:
К2
l2.
1
. Фронтальная
проекция К2
находится по принадлежности прямой l
:
К2
l2.
Видимость прямой на П2 определяем «по представлению»: рассматриваем горизонтальную проекцию совместно с направлением взгляда наблюдателя на П2 и видим, что при взгляде на П2 часть прямой правее точки К располагается за плоскостью и является невидимой.
5.3.2.Пересечение плоскостей, одна из которых – частного положения
Задача. Построить линию пересечения m двух плоскостей, одна из которых - проецирующая (рис.36).
Алгоритм решения
1. Линия пересечения принадлежит фронтально проецирующей плоскости, следовательно, фронтальная проекция линии совпадает с вырожденной проекцией плоскости: m2 = 2 .
2. Линия пересечения m принадлежит плоскости треугольника АВС, следовательно, она пересекает стороны треугольника АВ и АС в точках 1 и 2. Построив горизонтальные проекции этих точек по принадлежности сторонам треугольника и соединив их, получаем горизонтальную проекцию искомой линии пересечения m1 .
3. Видимость треугольника на П1 определяем так же , как и в предыдущей задаче, «по представлению»: рассматриваем фронтальную проекцию совместно с направлением взгляда наблюдателя на П1 и видим, что при взгляде сверху часть треугольника (А12) располагается ниже плоскости и является невидимой.
5.3.3. Пересечение прямой и плоскости общего положения
 (первая
основная позиционная задача)
(первая
основная позиционная задача)
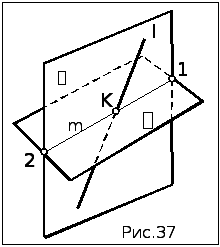
Алгоритм решения(рис.37)
Через заданную прямую l проводится проецирующая плоскость .
2. Строится линия m пересечения плоскостей и .
3.
Находится точка К
пересечения прямой l
с построенной линией пересечения m:
l
![]() К
К![]() m.
Это и есть искомая точка пересечения
прямой l
с плоскостью.
m.
Это и есть искомая точка пересечения
прямой l
с плоскостью.
 Задача.
Построить точку К
пересечения прямой l
с плоскостью
(АВС)
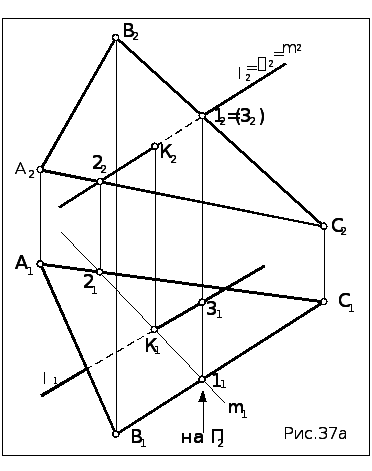
(рис.37а).
Задача.
Построить точку К
пересечения прямой l
с плоскостью
(АВС)
(рис.37а).
Т.к. заданные прямая и плоскость – общего положения, то применяем алгоритм решения первой основной позиционной задачи.
1. Прямую l заключаем во фронтально проецирующую плоскость : l2 =2.
2. Строим линию пересечения m плоскостей и :
2.1. Фронтальную проекцию m находим из условия её принадлежности плоскости : m m2 =2 ,
2.2. Горизонтальную проекцию m находим из условия её принадлежности плоскости : m пересекает стороны ВС и АС:
m
m
![]() ВС
=1, m
ВС
=1, m
![]() АС
=2.
АС
=2.
Фронтальные
проекции точек 1
и 2
находим как результат пересечения
одноименных проекций m,
ВС
и АС:
12=
m2
![]() В2С2,
22=
m2
В2С2,
22=
m2
![]() А2
С2,
а
горизонтальные – по принадлежности
сторонам треугольника: 11
В1С1,
21
А1С1
.Соединив
горизонтальные проекции точек 1
и 2,
получим горизонтальную проекцию линии
пересечения:
11
А2
С2,
а
горизонтальные – по принадлежности
сторонам треугольника: 11
В1С1,
21
А1С1
.Соединив
горизонтальные проекции точек 1
и 2,
получим горизонтальную проекцию линии
пересечения:
11
![]() m1
m1
![]() 21.
21.
3.
Находим точку пересечения прямой l
с
треугольником АВС
:
К1=
m1![]() l1,
К2
l2.
l1,
К2
l2.
4. Видимость прямой определяем с помощью конкурирующих точек. На прямой l берем точку 3, фронтально конкурирующую с точкой 1, по построению принадлежащей стороне ВС треугольника. Рассматриваем горизонтальную проекцию совместно с направлением взгляда на П2. Точка 1 (треугольник) ближе к наблюдателю и заслоняет точку 3(прямую l), следовательно, правее точки К (граница видимости) прямая l является невидимой. На П1 видимость можно определить аналогичным образом, но проще воспользоваться тем, что плоскость (АВС) – нисходящая, и у неё на П1 и П2 видны разные стороны, следовательно, и разные участки прямой l: на горизонтальной проекции невидимым является участок левее точки К.
