12.4.Развертка конической поверхности
Если задана поверхность прямого кругового конуса с радиусом основания R и высотой h, то развертка его боковой поверхности представляет собой круговой сектор, радиус которого равен длине образующей l конуса, а центральный угол = 3600 R/l.
Если конус усеченный, то строится его приближенная развертка – развертка усеченной n угольной пирамиды, вписанной в конус.
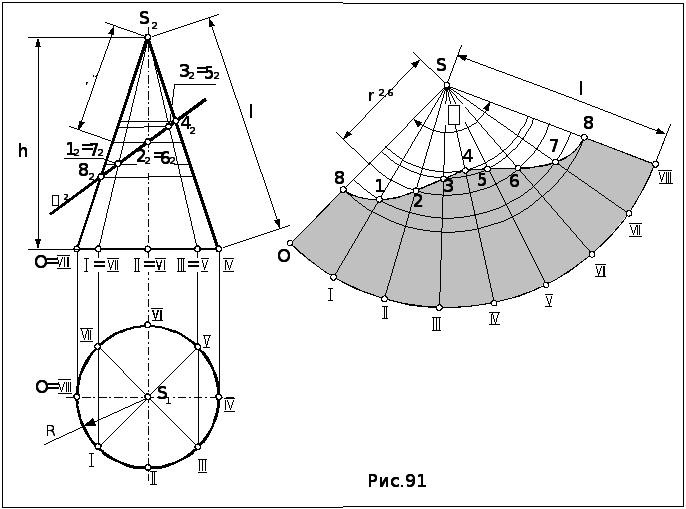
Задача. Построить развертку боковой поверхности конуса, усеченного плоскостью .
Алгоритм решения
1. Строим развертку прямого кругового конуса – круговой сектор с параметрами, указанными выше.
2. Вписываем в
конус правильную n
угольную (на
рис.91 – 8 угольную) пирамиду, для чего
делим окружность основания на 8 равных
частей, находим точки деления 0 - 
на П2
.и
соединяем полученные точки с вершиной
S.
3. Находим фронтальные проекции 12 …82 точек пересечения ребер плоскостью как результат пересечения вырожденной проекции плоскости 2 с проекциями ребер и проводим через найденные точки проекции параллелей конуса – отрезки, перпендикулярные оси конуса.
4. Делим на 8 равных частей дугу – развертку основания конуса и точки деления соединяем с вершиной S на развертке.
5. Строим на развертке точки пересечения ребер вписанной пирамиды с плоскостью как результат пересечения ребер с соответствующими проекциями параллелей на развертке. Параллели конуса развертываются в дуги, концентричные развертке основания, радиусы которых равны замеренному по очерковой образующей конуса расстоянию между фронтальной проекцией параллели и вершиной S2. Например, параллель, на которой расположены точки 2 и 6, разворачивается на развертке в дугу с центром в точке S и радиусом r2,6.
6. Построенные на
развертке точки 1…8
соединяем
плавной лекальной кривой. Фигура,
ограниченная этой кривой, разверткой
основания и участками ребер 0 и 
и будетразверткой боковой
поверхности конуса, усеченного плоскостью
. Чтобы
построить полную развертку усеченного
конуса, необходимо добавить еще НВ
основания и сечения.
ЛИТЕРАТУРА
1. Начертательная геометрия. Конспект лекций для студентов машиностроительных специальностей.- Мариуполь, 1999.- 147 с.
2. Четверухин Н.Ф. Начертательная геометрия / В.С.Левицкий, З.И.Прянишникова, А.М.Тевлин, Г.И.Федотов.- М.: Высшая школа, 1963.- 420 с.
3. Фролов С.А. Начертательная геометрия / С.А.Фролов.- М.: Машиностроение, 1983. 240 с.
4. Рабочая тетрадь по начертательной геометрии.- Мариуполь, 2004.-46 с.
5. Методические указания по начертательной геометрии и черчению для студентов заочной формы обучения.- Мариуполь, 2004.- 49 с.