1. Методы проецирования

Для построения чертежа применяются различные методы проецирования.

1.1.Центральное проецирование

В аппарат центрального прое-цирования (параметры, выбираемые проектировщиком) входят:

• плоскость проекций П' ,

• центр проекций S.

Чтобы построить центральную про-екцию точки А пространства, нужно через центр S и точку А провести прямую, называемую проецирующей. Точка пересечения проецирующей прямой с плоскостью проекций и будет центральной проекцией точки А - А'.

1.2.Параллельное и ортогональное проецирование

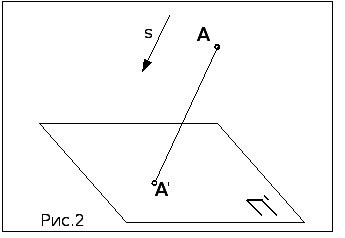
Аппарат параллельного проецирования:

• плоскость проекций П^',

• направление проецирования s.

Чтобы построить параллельную про-екцию точки А пространства, нужно через точку А провести проецирующую прямую, параллельную s. Точка пересе-чения проецирующей прямой с плос-костью проекций и будет параллель-ной проекцией точки А - А'.

Если направление проецирова-ния перпендикулярно плоскости проек-ций, то такое проецирование называется ортогональным.

1.3.Свойства ортогонального проецирования

1. Проекцией точки является точка (рис.2.)

2. Проекцией прямой, не перпендикулярной плоскости проекций, является прямая, а прямой, перпендикулярной плоскости проекций – точка (рис.3).

3. Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой (рис.3).

4. Если прямые параллельны, то их про-екции параллельны или совпадают (рис.4).

5. Отношение отрезков, лежащих на одной прямой или на параллель-ных прямых, равно отношению проекций этих отрезков: [АС]:[ВС] = [A'C']:[В'С'] (рис.3.)

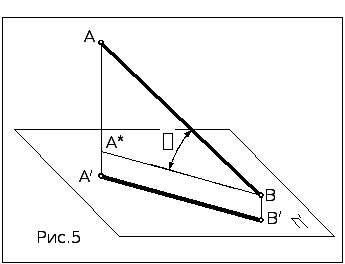6. Длина проекции отрезка, наклон-ного к плоскости проекций, мень-ше длины отрезка в пространстве и равна [A^/B^/] = [AB]× Cos α (рис.5), что следует из треуголь-ника АВА*.

7.Если одна сторона прямого угла па-раллельна плоскости проекций, а дру-гaя к ней не перпендикулярна, то пря-мой угол проецируется в натураль-ную величину (рис.6):

если прямая перпендикулярна двум пересекающимся прямым плоскости , то она перпендикулярна этой плоскости и любой прямой ей принадлежащей:

(АВ)(ВС) и (АВ)(ВВ^/), то (АВ).

(А^/В^/)║(АВ), следовательно(А^/В^/) и (В^/С^/).(А^/В^/)

8. Проекция фигуры не изменяется при параллельном переносе плос-кости проекций.

1.4.Обратимость чертежа

Проекции точки А' (рис.2) соответствует бесконечное множество точек А в простран-стве, расположенных на проецирующей прямой АА', т.е. реконструировать однозначно точку в пространстве невозможно и такой чертеж не обладает свойством обратимости. Впервые задачу создания обратимого (комплексного) чертежа решил французский учёный Гаспар Монж, предложивший ортогонально проецировать точку на две и более взаимно перпендикулярных плоскости проекций. Стандартом Единой системы конструкторской документации (ЕСКД) установлено 6 основных плоскостей проекций, образующих грани куба.

2. Трёхкартинный чертеж точки

2.1.Аппарат проецирования

Плоскости проекций:

• П₁ – горизонтальная,

• П₂ – фронтальная,

• П₃ – профильная.

Оси проекций: x₁₂, y_13, z₂₃.

Чтобы построить чертеж точки, методом ортогонального проецирования находятся последовательно проекции точки: А₁ – гори-зонтальная, А₂ – фронтальная, А₃ – профильная, а также А₁₂ , А₁₃ , А₂₃ – проекции точки на осях проекций.

Параметры точки: высота h, глубина f, широта р – расстояния от точки до горизонтальной, фронтальной и профильной плоскости проекций соответственно.

Для получения плоского изображения (чертежа) пространственную конструкцию из плоскостей проекций мысленно разрезаем по оси y₁₃, П₁ вращаем вокруг оси x₁₂ вниз от наблюдателя до совмещения с П₂ , а П₃ вращаем вокруг оси z₂₃ вправо от наблюдателя до совмещения с П₂, как это показано на рис.7. Ломаные линии А₁А₁₂А₂, А₁А₁₃А₃ и А₂А₂₃А₃ превращаются в прямые, перпендикулярные соответствующим осям проекций и называемые линиями связи.

Для удобства построений проведем константу К_о чертежа под 45^о к осям проекций через точку их пересечения.

Тогда трёхкартинный чертеж точки представит собой прямоугольник, стороны которого – линии связи, перпендикулярные соответствующим осям проекций; три вершины прямоугольника – проекции точки, а четвертая - точка перелома линии связи на константе комплексного чертежа К_о (рис.8)