10.4.Пересечение поверхности прямой линией

В общем случае для построения точек пересечения прямой с поверхностью применяется метод вспомогательных секущих плоскостей по следующему алгоритму(рис.78):

1. Прямая l заключается в плоскость , пересекающую поверхность Ф по геометрически простой линии: l   Ф.

2. Строится линия m пересечения поверхности Ф вспомогательной плоскостью  :. m = Ф.

3. Искомые точки 1 и 2 находим как результат пересечения заданной прямой l с построенной линией пересечения m: 1,2 = l m.

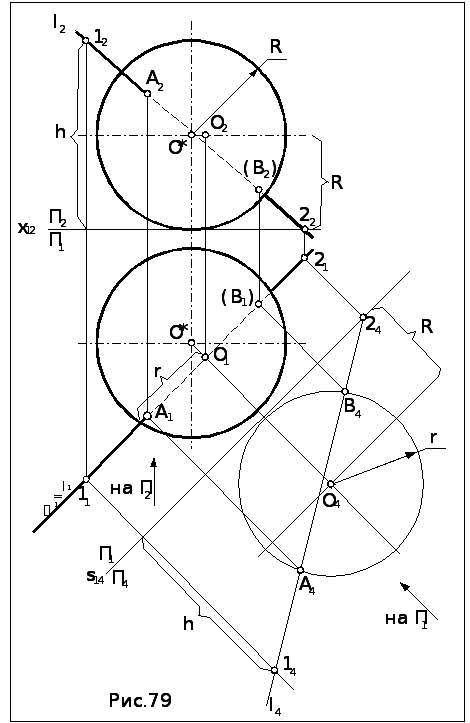
Задача. Построить точки пересечения прямой l с поверхностью сферы Ф (О^*,R) (рис.79).

Алгоритм решения

1. Заключаем прямую l в горизонтально проецирующую плоскость  : l₁= _1.

2. Строим линию пересечения плоскости  со сферой – окружность (О, r). На П₁ окружность проецируется в виде отрезка, расположенного внутри очерка сферы на вырожденной проекции ₁ . Разделив отрезок пополам, находим проекцию центра О₁ и радиус r сечения. На П₂ окружность проецируется в виде эллипса, т.к.  наклонена к П₂ . Построение эллипса - графически довольно сложная задача. Поэтому для упрощения решения вводим дополнительную плоскость П₄, расположив её параллельно  , и переходим к новой системе плоскостей проекций П₁ / П₄ : П₂ П₄ ,

П₁ / П₂ (x₁₂) П₁ /П₄ ( s₁₄ ₁ )

Строим в П₄ проекцию окружности, находя проекцию её центра по алгоритму построения точки в дополнительную плоскость.

Взяв на прямой l произвольные точки 1 и 2, строим их проекции на П₄ , соединив которые получаем проекцию прямой l₄

3. Находим точки А и В пересечения прямой l со сферой, сначала на П₄ как результат пересечения l₄ с проекцией окружности (О₄ , r ), а затем по принадлежности прямой l на остальных плоскостях проекций.

4. Видимость точек А и В и прямой l определяем по представлению, рассматривая проекции совместно с направлением взгляда на соответствующую плоскость проекций, как это показано на рис.78.

11. Взаимное пересечение поверхностей

11.1.Пересечение криволинейной и гранной поверхностей

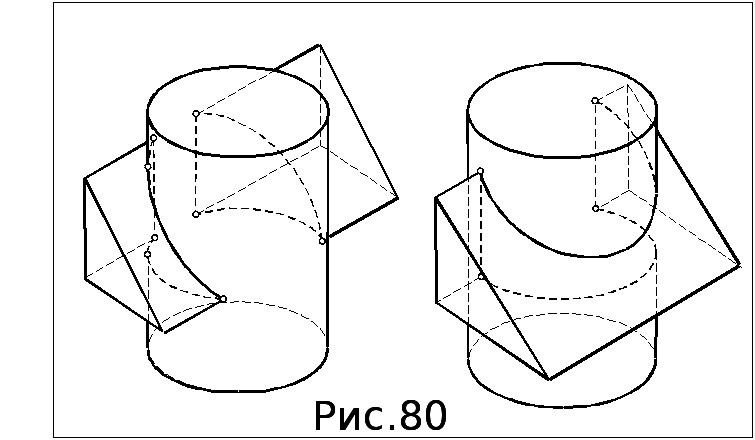Линией пересечения (ЛП) криволинейной и гранной поверхностей является пространственная замкнутая ломаная, вершинами которой являются точки пересечения ребер многогранника с криволинейной поверхностью, а звенья - линии пересечения криволинейной поверхности с гранями многогранника. В случае врезки ЛП состоит из одной ломаной, в случае проницания - из двух (рис.80).

Особые точки ЛП:

• вершины ломаной – точки пересечения ребер многогранника с поверхностью вращения;

• опорные точки (граничные точки видимости) - точки пересечения очерковых образующих криволинейной поверхности с гранной поверхностью;

• особые точки кривых - звеньев ЛП: центры, вершины, точки на концах осей и т.д.

Построение ЛП сводится к двум выше уже рассмотренным выше задачам: а) построить точки пересечения прямой с поверхностью и б) построить сечение поверхности плоскостью.

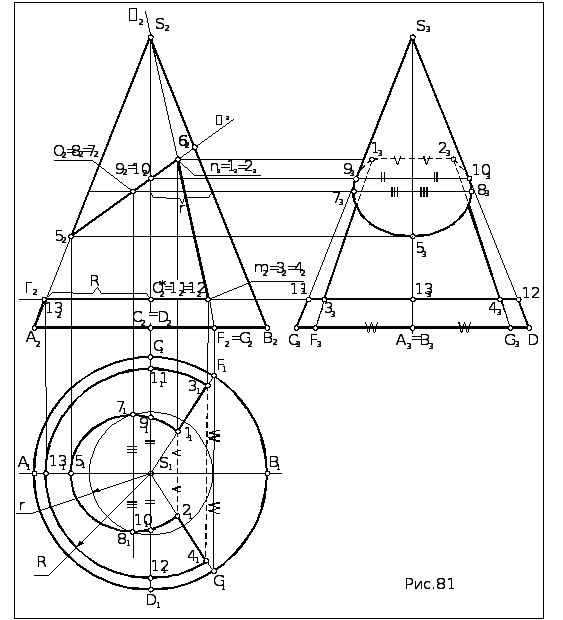
Задача. Построить проекции конуса с призматическим вырезом (рис.81).

Алгоритм решения

1. Определяем тип линии пересечения (ЛП). Т.к. ни одна из поверхностей не пересекает другую полностью, то данный случай - врезка и ЛП состоит из одной ломаной. Звенья ЛП - конические сечения: грань призмы Г(Г₂ ), перпендикулярная оси конуса, пересекает конус по дуге окружности; грань призмы (₂) , плоскость которой проходит через вершину конуса, - по образующим конуса; грань призмы  (₂) , наклоненная к оси конуса (),- по дуге эллипса.

Т.к. грани призмы фронтально проецирующие, то на П₂ проекция ЛП совпадает с проекцией призматического выреза.

2. Находим особые точки ЛП сначала на известной фронтальной проекции:

-вершины ломаной – точки пересечения ребер n и m c поверхностью конуса - совпадают с проекциями самих ребер, т.к. ребра – фронтально проецирующие: n₂ = 1₂ =2₂, m₂ = 3₂ =4₂.

-центр О(О₂) и точки на концах осей эллипса. Продлив грань  (₂) до пересечения с очерковой образующей S₂ B₂ находим фронтальную проекцию большой оси эллипса 5₂ 6₂ , разделив которую пополам находим центр О(О₂) и точки 7₂= 8₂ на концах малой оси.

- граничные точки видимости находим как результат пересечения вырожденных про-екций граней призматического отверстия с очерковыми образующими конуса: граничные точки видимости на П₂ – 5₂ = S₂А₂ ₂ , 13₂ = S₂А₂Г₂ , граничные точки видимости на

П₃ – 9₂ = S₂ C₂ ₂ , 10₂ = S₂ D₂ ₂ , 11₂ = S₂ C₂ Г₂ , 12₂ = S₂ D₂ Г₂.

На остальных проекциях найденные на П₂ точки находим либо по их принадлеж-ности образующим, на которых они расположены, либо по их принадлежности конусу. Например, точки 7 и 8 находим, проведя параллель радиуса r. При этом для достижения требуемой точности построений не рекомендуется пользоваться постоянной чертежа к₀ и ломаными линиями связи между П₁ и П₃ (см. задачу на рис.77).

3. Случайные точки (на дуге эллипса) выбираем произвольно на П₂ , а другие их проекции находим по принадлежности поверхности конуса, как точки 7,8.

4. Построенные точки соединяем с учетом их видимости на проекциях, определяя ви-димость по представлению. При взгляде сверху ЛП видима полностью, не видны только ребра m и n отверстия. На П₂ видимые и невидимые части ЛП совпадают. При взгляде слева (на П₃) видимы части ЛП, лежащие на левой половине конуса, а также участки пря-мых (13) и (24) из-за отсутствия материала, их закрывающего.