
- •Оглавление
- •1. Методы проецирования
- •1.2.Параллельное и ортогональное проецирование
- •1.3.Свойства ортогонального проецирования
- •1.4.Обратимость чертежа
- •2. Трёхкартинный чертеж точки
- •2.1.Аппарат проецирования
- •2.2.Конкурирующие точки
- •3. Чертеж прямой
- •3.1.Положение прямой относительно плоскостей проекций
- •3.1.1.Прямая общего положения.
- •3.1.2.Прямая уровня
- •3.1.3.Проецирующая прямая
- •3.2.Взаимное положение прямых
- •4. Комплексный чертеж плоскости
- •4.1.Положение плоскости относительно плоскостей проекций
- •4.1.1.Плоскость общего положения
- •4.1.2.Проецирующая плоскость
- •4.1.3.Плоскость уровня
- •4.2.Принадлежность прямой и точки плоскости
- •4.3.Прямые особого положении в плоскости
- •4.3.1.Прямая уровня плоскости
- •4.3.2.Прямая наибольшего наклона плоскости к какой-либо плоскости проекций
- •5. Взаимное положение прямой и плоскости, двух плоскостей
- •5.1.Параллельность прямой и плоскости
- •5.2.Параллельность плоскостей
- •5.3.Пересечение прямой и плоскости
- •5.3.1.Пересечение прямой и плоскости частного положения
- •5.3.2.Пересечение плоскостей, одна из которых – частного положения
- •5.4.Пересечение плоскостей общего положения (вторая основная позиционная задача
- •5.5.Перпендикулярность прямых и плоскостей
- •5.5.1.Перпендикуляр к плоскости
- •5.5.2.Плоскость, перпендикулярная прямой
- •5.5.3.Взаимно перпендикулярные прямые
- •5.5.4.Взаимно перпендикулярные плоскости
- •6. Способы преобразования чертежа
- •6.1.Замена плоскостей проекций
- •6.2.Плоскопараллельное перемещение
- •6.3.Вращение вокруг проецирующей прямой
- •6.4.Вращение вокруг прямой уровня
- •7. Многогранники
- •7.1.Пересечение многогранника плоскостью
- •7.2.Пересечение многогранника прямой
- •7.3.Взаимное пересечение многогранников
- •8. Кривые линии
- •8.11.Плоские кривые. Касательные и нормали
- •8.2.Основные свойства проекций плоских кривых линий
- •8.3.Проецирование окружности
- •8.4.Цилиндрическая винтовая линия
- •9. Криволинейные поверхности
- •9.1.Очерк поверхности
- •10. Поверхности вращения
- •10.1.Основные линии поверхности вращения.
- •10.3.Построение сечения поверхности вращения плоскостью
- •10.4.Пересечение поверхности прямой линией
- •11. Взаимное пересечение поверхностей
- •11.2.Пересечение поверхностей вращения второго порядка
- •11.2.1.Способ секущих плоскостей (рис.82)
- •11.2.2.Способ концентрических секущих сфер
- •12. Развертки поверхностей
- •12.1.Развертка призмы
- •12.2.Развертка пирамиды
- •12.3.Развертка цилиндрической поверхности
- •12.4.Развертка конической поверхности
10. Поверхности вращения
Поверхностью
вращения называется поверхность,
образованная при вращении линии
(образующей) вокруг неподвижной оси. В
инженерной практике поверхности вращения
задаются, как правило, своими очерками
 (рис.73,74).
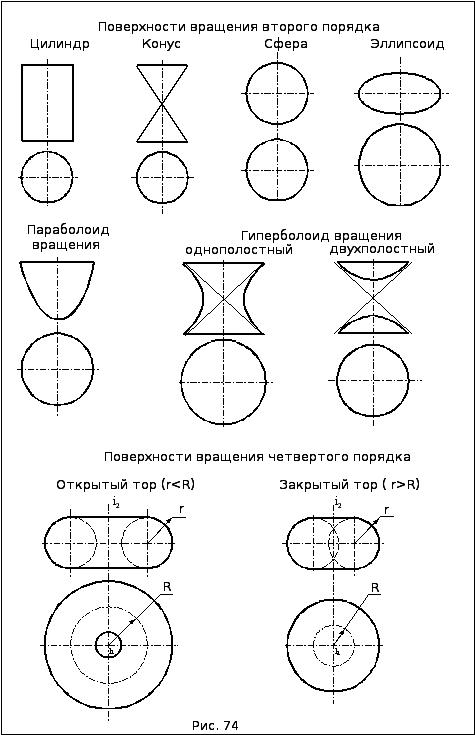
На рис. 74 показаны наиболее часто
встречающиеся в инженерной практике
поверхности вращения.
(рис.73,74).
На рис. 74 показаны наиболее часто
встречающиеся в инженерной практике
поверхности вращения.
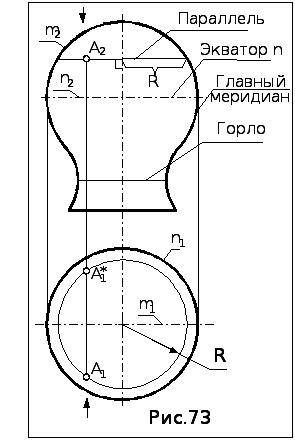
10.1.Основные линии поверхности вращения.
Параллель - сечение поверхности вращения плоскостью, перпендикулярной оси вращения. Представляет собой окружность, которая на плоскость проекций, перпендикулярную оси, проецируется в натуральную величину, а в плоскость, параллельную оси, - в виде отрезка, перпендикулярного проекции оси и равного диаметру параллели. Наибольшая из близлежащих параллелей называется экватором, наименьшая - горлом.
Меридиан - сечение поверхности вращения плоскостью, проходящей через ось вращения.
Меридиан, расположенный в плоскости, параллельной плоскости проекций, называется главным меридианом и определяет очерк поверхности в этой плоскости.
С помощью этих линий «берутся» (строятся) точки, принадлежащие поверхности. При этом используется признак принадлежности точки поверхности:
точка принадлежит поверхности, если она ле- жит на линии, этой поверхности принадлежащей.
Например, с помощью параллели радиуса R на поверхности построены проекции точки А: через заданную фронтальную проекцию А2 проведена проекция параллели, определен её радиус и построена её горизонтальная проекция, по принадлежности которой найдена горизонтальная проекция А1. При этом заданному положению А2 соответствуют два положения горизонтальной проекции точки : А1, если точка А видима на П2, и А1*, если она на П2 невидима.
10.2.Пересечение криволинейной поверхности плоскостью
Поверхности вращения второго порядка пересекаются плоскостью по кривым второго порядка.
10.2.1.Cферические сечения. При пресечении сферы плоскостью всегда получается окружность.
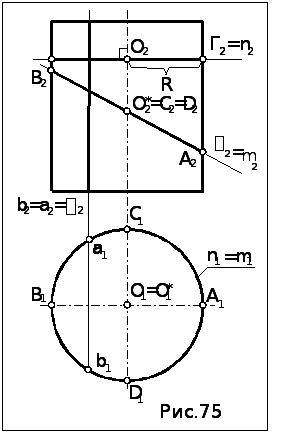 10.2.2.Цилиндрические
сечения. Вид
цилиндрического сечения (рис.75) зависит
от положения секущей плоскости
относительно оси цилиндра:
10.2.2.Цилиндрические
сечения. Вид
цилиндрического сечения (рис.75) зависит
от положения секущей плоскости
относительно оси цилиндра:
плоскость перпендикулярна оси цилиндра – в сечении – окружность с центром О на оси i и радиусом, равным радиусу цилиндра Гi , Г
 Фцил=
окружность n(О,
R);
Фцил=
окружность n(О,
R);плоскость параллельна оси цилиндра – в сечении две параллельных прямых – образующих цилиндра
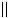 i
,
i
,
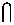 Фцил
= a
и b;
Фцил
= a
и b;плоскость наклонена к оси цилиндра – в сечении - эллипс с центром О* на оси i с большой осью АВ, величина которой зависит от угла наклона плоскости к оси, и малой осью CD, равной диаметру цилиндра
![]()
![]() i
,
i
,
![]() Фцил
= эллипс (О*,
AB,
CD
=R).
Фцил
= эллипс (О*,
AB,
CD
=R).
Цилиндрическая поверхность является проецирующей к плоскости проекций, перпендикулярной к оси цилиндра, поэтому в эту плоскость (на рис.74 в П1) сечения цилиндра проецируются на окружность - вырожденную проекцию (очерк) поверхности
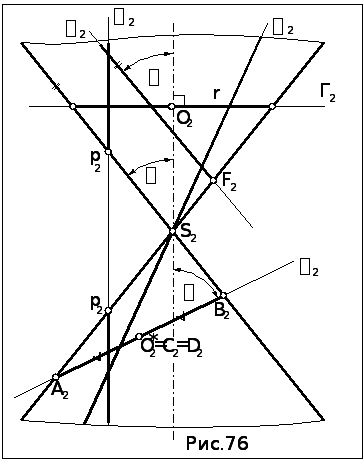 10.2.3.Конические
сечения.
Вид конического сечения зависит от
следующих факторов (рис.76):
10.2.3.Конические
сечения.
Вид конического сечения зависит от
следующих факторов (рис.76):
Положение секущей плоскости относительно вершины конуса:
если
плоскость проходит через вершину конуса
(
![]() S)
-
в сечении две пересекающиеся прямые
(образующие конуса);
S)
-
в сечении две пересекающиеся прямые
(образующие конуса);
если плоскость не проходит через вершину - в сечении кривые второго порядка.
Угол между секущей плоскостью и осью конуса:
если угол - 90°( Г i), то в сечении окружность (О, r) (параллель конуса);
если угол не равен 90° - в сечении эллипс, парабола или гипербола.
3. Соотношение между углом наклона секущей плоскости к оси конуса и углом между осью конуса и его образующей:
а)
,
![]() Фкон
=
эллипс; большая ось эллипса – АВ,
малая – CD,
центр эллипса О*
не
лежит на оси конуса и находится делением
АВ
пополам (А2О2
= В2О2).
Фкон
=
эллипс; большая ось эллипса – АВ,
малая – CD,
центр эллипса О*
не
лежит на оси конуса и находится делением
АВ
пополам (А2О2
= В2О2).
б)
=
,
![]() Фкон
=
парабола с вершиной F;
Фкон
=
парабола с вершиной F;
в)
,
![]() Фкон
=
гипербола с вершинами в точках Р.
Фкон
=
гипербола с вершинами в точках Р.
