
- •Н. М. Качуровская
- •Содержание
- •Введение
- •Правила оформления контрольных работ
- •Контрольная работа № 1
- •Эпюр 1. Точка, прямая, плоскость Содержание эпюра
- •Пояснения к выполнению эпюра 1 Задача 1
- •Задача 2
- •Эпюр 2. Пересечение поверхностей и построение теней Содержание эпюра
- •Варианты заданий к эпюру 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Задача 8
- •Задача 9
- •Контрольная работа № 2
- •Эпюр 3. Пересечение поверхностей1 Содержание эпюра
- •Варианты заданий к эпюру 3
- •Примеры построения поверхностей вращения
- •Пояснения к выполнению эпюра 3 Задача 1
- •Задача 2
- •Эпюр 4. Геометрическое формообразование поверхностей
- •Задача 2
- •Задача 3
- •Экзаменационные задания и примеры решения типовых задач Построение проекций точки
- •Задача 1
- •Знаки координат точек, находящихся в разных октантах
- •Задача 2
- •Прямая, плоскость. Построение проекций прямой, плоскости. Нахождение натуральной величины прямой, плоскости. Метрические задачи Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Задача 8
- •Задача 9
- •Задача 10
- •Задача 11
- •Задача 20
- •Задача 21
- •Задача 22
- •Задача 23
- •Задача 24
- •Задача 25
- •Задача 26
- •Задача 27
- •Задача 28
- •Задача 29
- •Задача 30
- •Задача 31
- •Задача 32
- •Первая позиционная задача. Нахождение точки пересечения прямой и плоскости. Нахождение расстояния от точки до плоскости Задача 38
- •Задача 39
- •Задача 40
- •Задача 41
- •Задача 42
- •Задача 43
- •Задача 44
- •Задача 52
- •Задача 57
- •Многогранные и кривые поверхности. Нахождение точки пересечения прямой и поверхности. Нахождение линии пересечения плоскости и поверхности. Нахождение линии пересечения поверхностей Задача 58
- •Задача 59
- •Задача 60
- •Задача 61
- •Задача 62
- •Задача 72
- •Задача 77
- •Задача 82
- •Задача 83
- •Задача 84
- •Заключение
- •Список литературы
- •Наталья Михайловна Качуровская
Пояснения к выполнению эпюра 1 Задача 1
В первой задаче контрольной работы требуется найти расстояние от точки Р до плоскости треугольника ABC. Кратчайшее расстояние от точки до плоскости есть перпендикуляр, опущенный из данной точки на плоскость.
Этап 1 (рис. 3). Проведем фронтальную проекцию горизонтали (h2) из вершины В2 треугольника ABC параллельно оси Х1,2 и найдем ее горизонтальную проекцию (h1), используя ее точку пересечения со стороной АС. Затем проведем горизонтальную проекцию фронтали (f1) из вершины С1 ΔАВС параллельно оси Х1,2 и найдем ее фронтальную проекцию (f2), используя ее точку пересечения со стороной АВ. Из точки Р2 опускаем перпендикуляр на f2 и из точки Р1 опускаем на h1.
Этап 2 (рис. 4). Необходимо найти точку пересечения перпендикуляра, опущенного из точки Р на плоскость, заданную ΔАВС. Для этого пропускаем через фронтальную проекцию перпендикуляра вспомогательную фронтально-проецирующую плоскость и находим точки ее пересечения со стороной А2С2 (32) и со стороной В2С2 (42). По проекционным связям находим горизонтальные проекции этих точек (31А1С1, 41В1С1). Пересечение прямой 3141 и горизонтальной проекции перпендикуляра, опущенного из точки Р1, и есть искомая точка пересечения (К1). Используя проекционную связь, находим точку К2 на перпендикуляре, который опущен из точки Р2. Таким образом, мы нашли проекции точки пересечения перпендикуляра, опущенного из точки Р на плоскость, заданную ΔАВС, на обеих проекциях.

Рис. 3. Этап 1
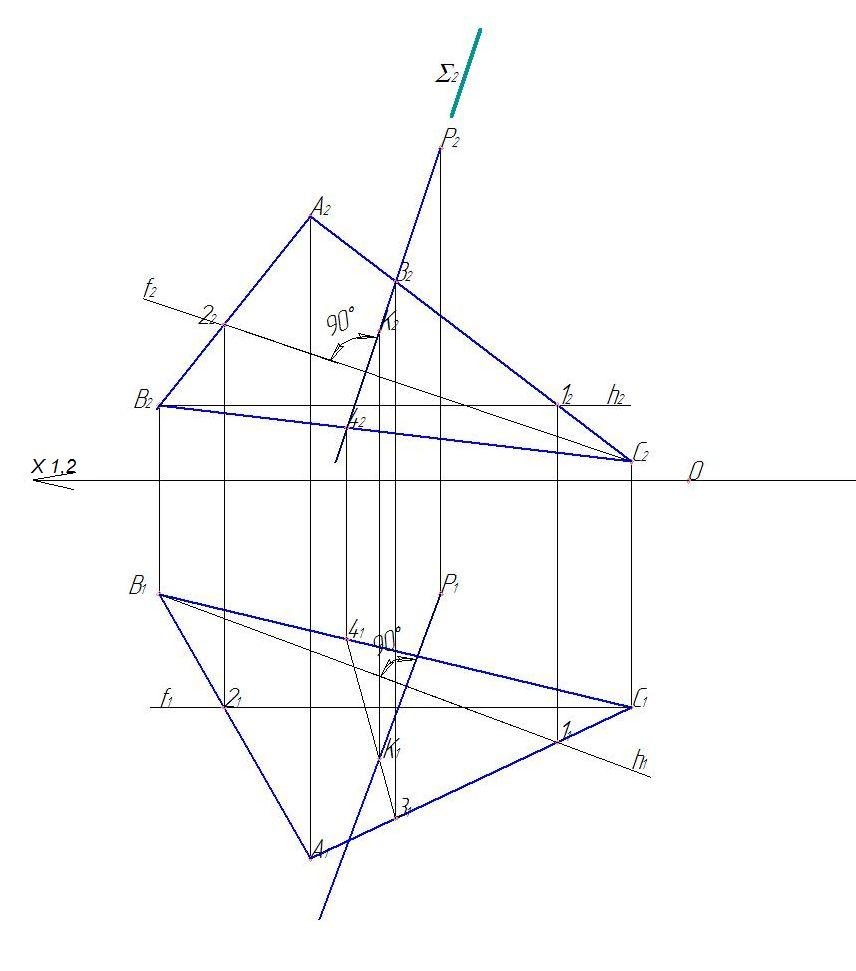
Рис. 4. Этап 2
Этап 3 (рис. 5). Следующий этап выполнения задания содержит в себе определение видимости перпендикуляра РК относительно плоскости АВС.
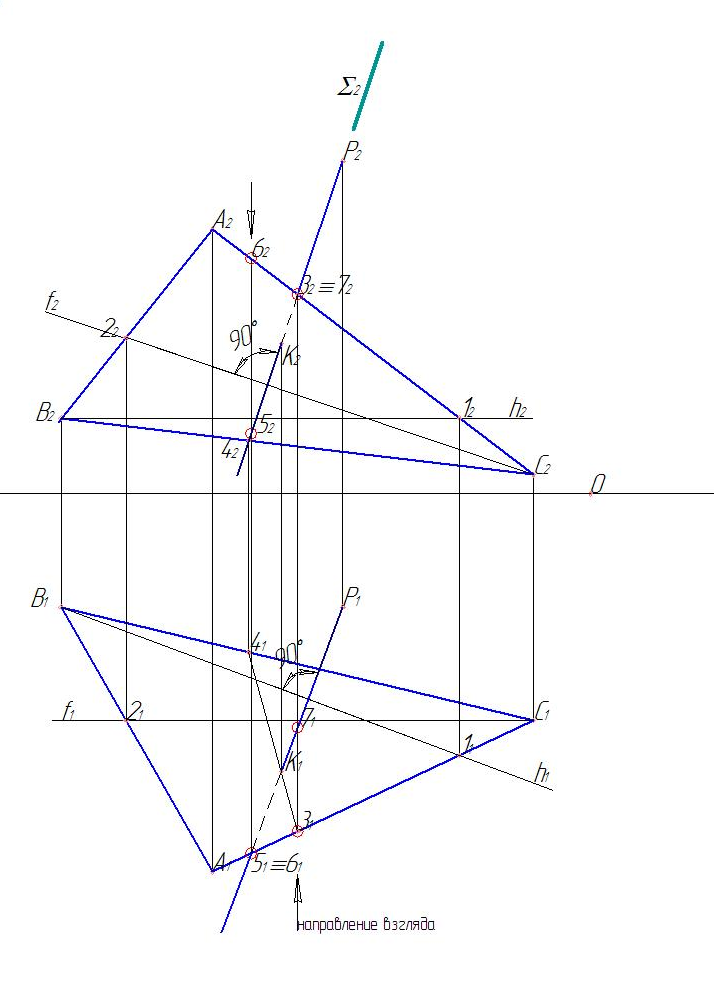
Рис. 5. Этап 3
Чтобы определить видимость перпендикуляра, берем две конкурирующие точки скрещивающихся прямых 32А2С2 и 72Р2К2 и находим их на соответствующих горизонтальных проекциях прямых 31А1С1 и 71Р1К1. Смотрим на них по стрелке направления взгляда. Первой встречается точка 31А1С1, а затем точка 71Р1К1. Вывод делаем на фронтальной плоскости проекций, откуда брали конкурирующие точки: из двух конкурирующих точек раньше встречается точка, принадлежащая плоскости АВС, следовательно, на рассматриваемом участке проекция перпендикуляра Р2К2 невидимая до точки пересечения, а после точки пересечения она становится видимой. Аналогично определяем видимость проекции перпендикуляра на горизонтальной плоскости проекций.
Этап 4 (рис. 6). Определяем натуральную величину перпендикуляра РК. Для этого к отрезку Р2К2 в точке Р2 восстанавливаем перпендикулярный отрезок (пока произвольной длины). Переходим на горизонтальную плоскость проекций и находим расстояние от точки К1 до Р1 как разность их высот по отношению к оси Х1,2 (Р1К1). Найденное расстояние откладываем на восстановленном перпендикуляре к отрезку Р2К2 в точке Р2 на фронтальной плоскости проекций. Отмечаем точку Р0. Точку Р0 соединяем с точкой К2. Отрезок Р0К2 является натуральной (истинной) величиной перпендикуляра РК к плоскости, заданной ΔАВС. Этот способ нахождения истинной величины отрезка прямой называется способом прямоугольного треугольника.
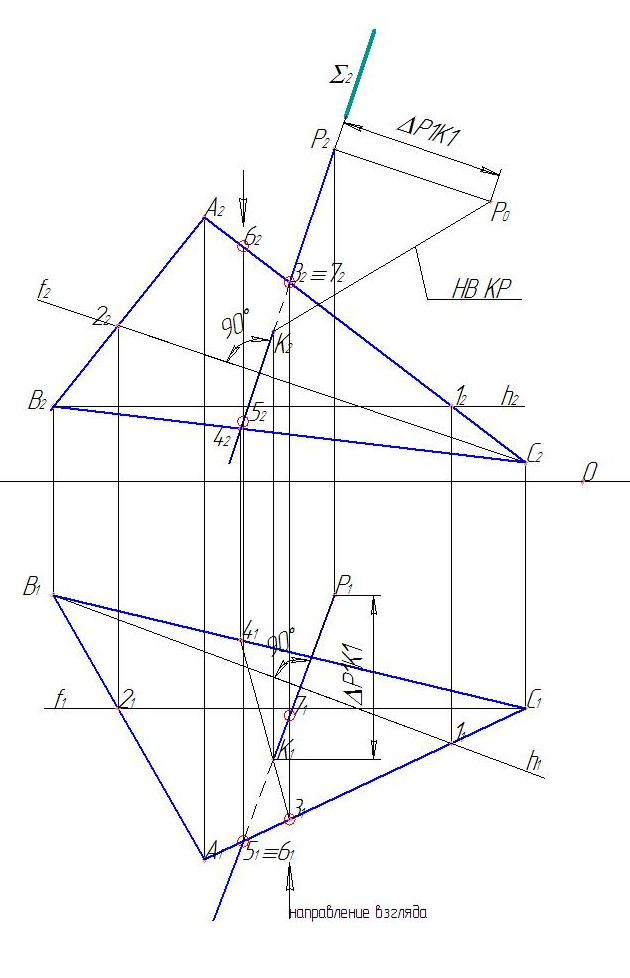
Рис. 6. Этап 4
