Задача 2

Во второй задаче требуется построить развертку призмы с нанесением линии пересечения.

Этап 1. Чтобы построить развертку призмы с полученным сечением, необходимо знать натуральные размеры всех ее сторон. Грань АВСD является горизонтальной плоскостью уровня, поэтому проецируется на горизонтальную плоскость в натуральную величину, а все остальные грани являются плоскостями общего положения (рис. 66).

Вынесем проекции призмы с построенным сечением на свободное поле чертежа. Методом замены плоскостей найдем натуральную величину граней МАСК и ВDЕN.

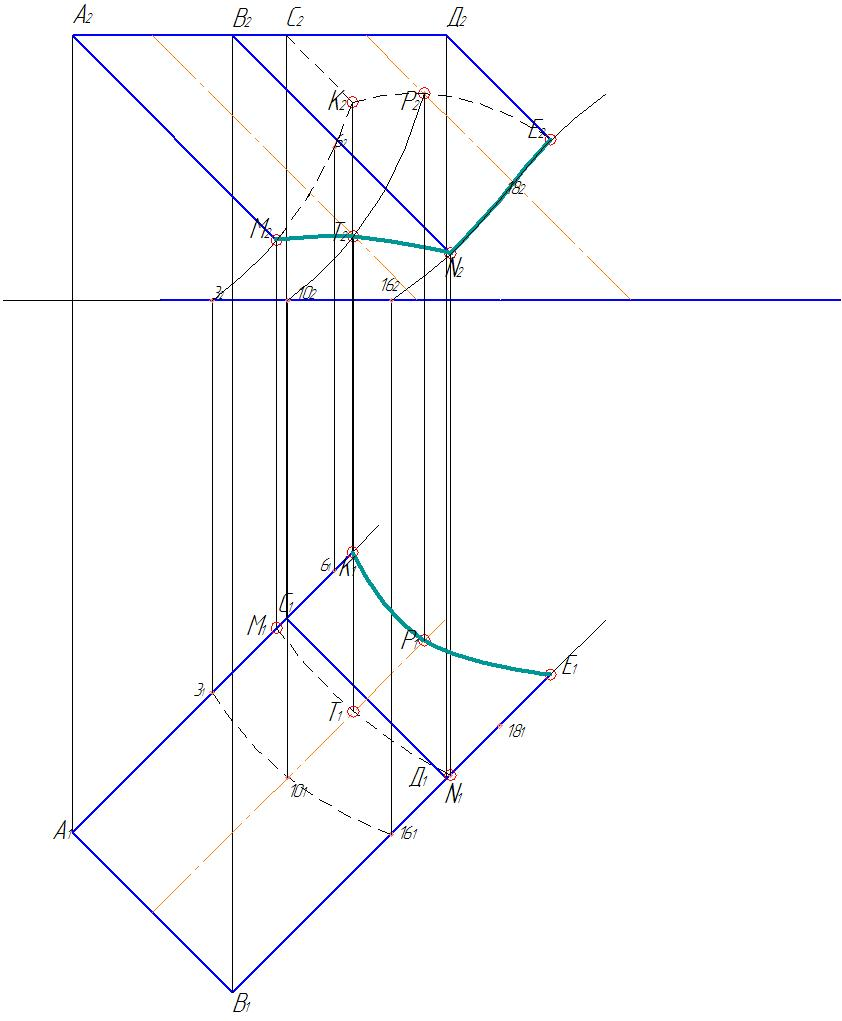
Рис. 66. Проекции призмы с сечением

Введем новую плоскость П4 параллельно граням АМКС (ВDЕN), которые являются горизонтально-проецирующими и проецируются на плоскость П1 в виде прямых линий. На рисунке 67 показано построение натуральной величины грани АМКС. Новая плоскость П4 заменяет фронтальную плоскость П2, поэтому новые значения для точек А, М, С, К берутся с фронтальной проекции. Для определения кривизны стороны МК использована точка 6 (точка может быть произвольной, но лежащей на кривой М2К2).

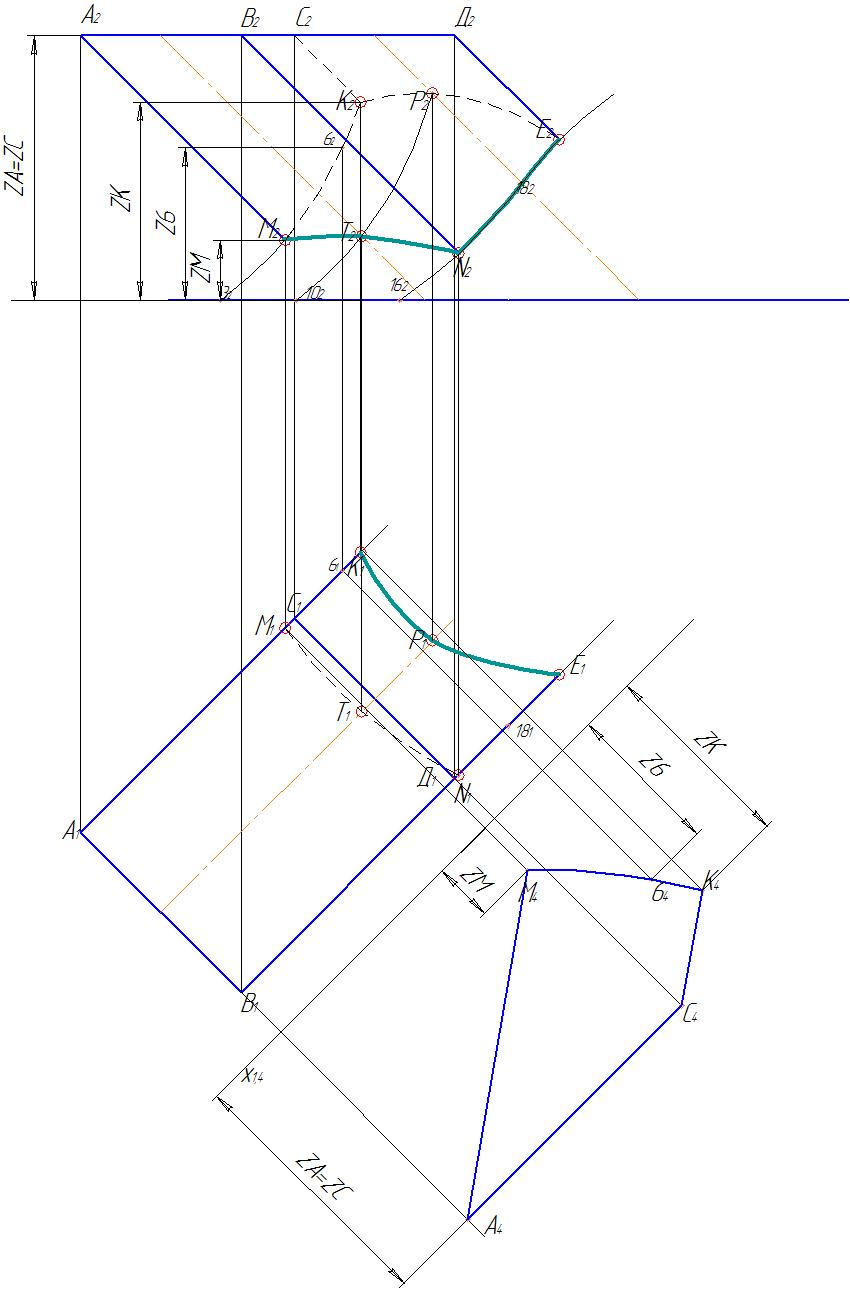
Рис. 67. Нахождение натуральной величины грани призмы

Аналогично находим натуральную величину грани ВDЕN (рис. 68). Для построения кривизны стороны NЕ используем точку 18 (точка может быть произвольной, но лежащей на кривой N2Е2).

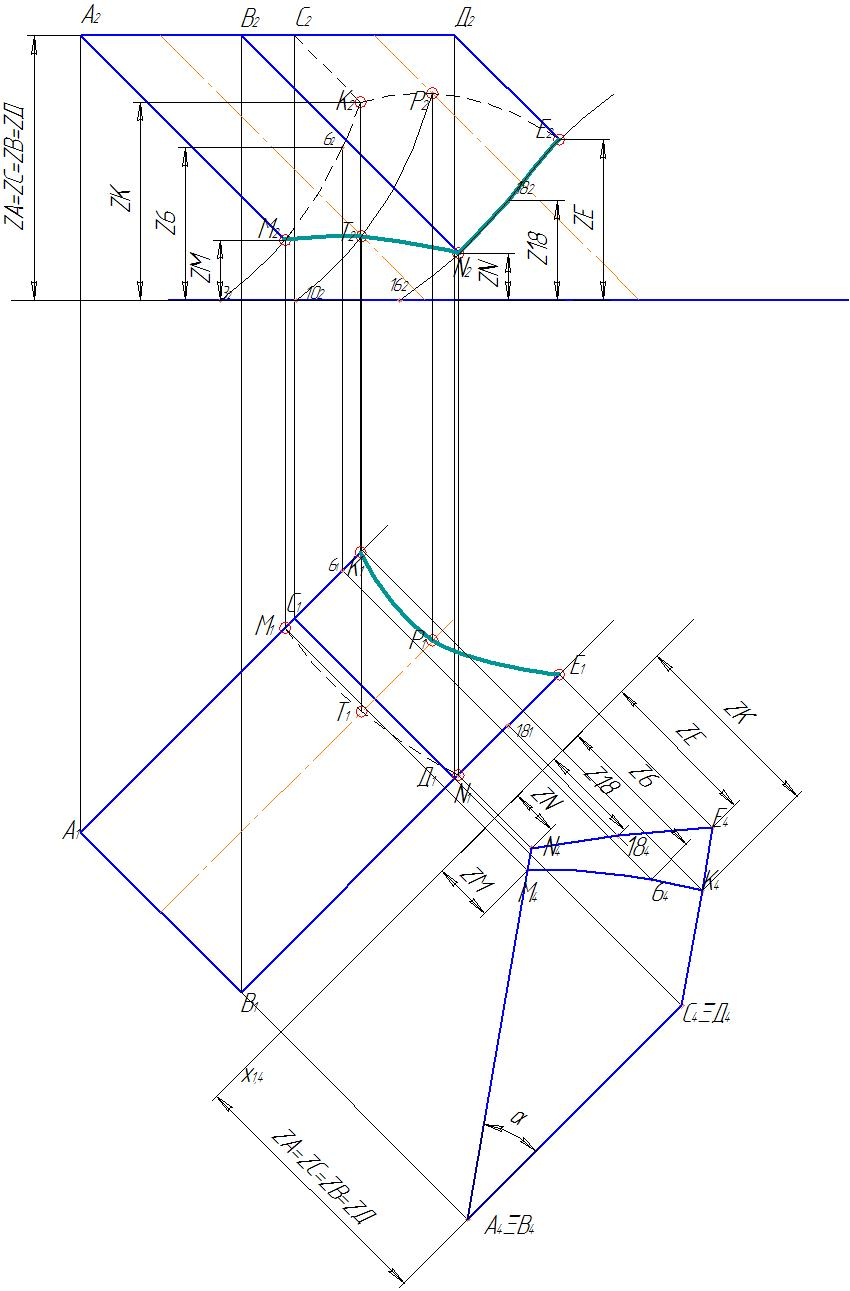
Рис. 68. Нахождение натуральной величины грани ВNЕD

Этап 2. Выполнение развертки призмы начнем с построения верхнего основания АВСD. Оно имеет форму прямоугольника АСDВ, является горизонтальной плоскостью уровня и проецируется на горизонтальную плоскость проекций в натуральную величину. Боковые грани строим, используя проекцию, построенную на плоскости П4 (рис. 69).

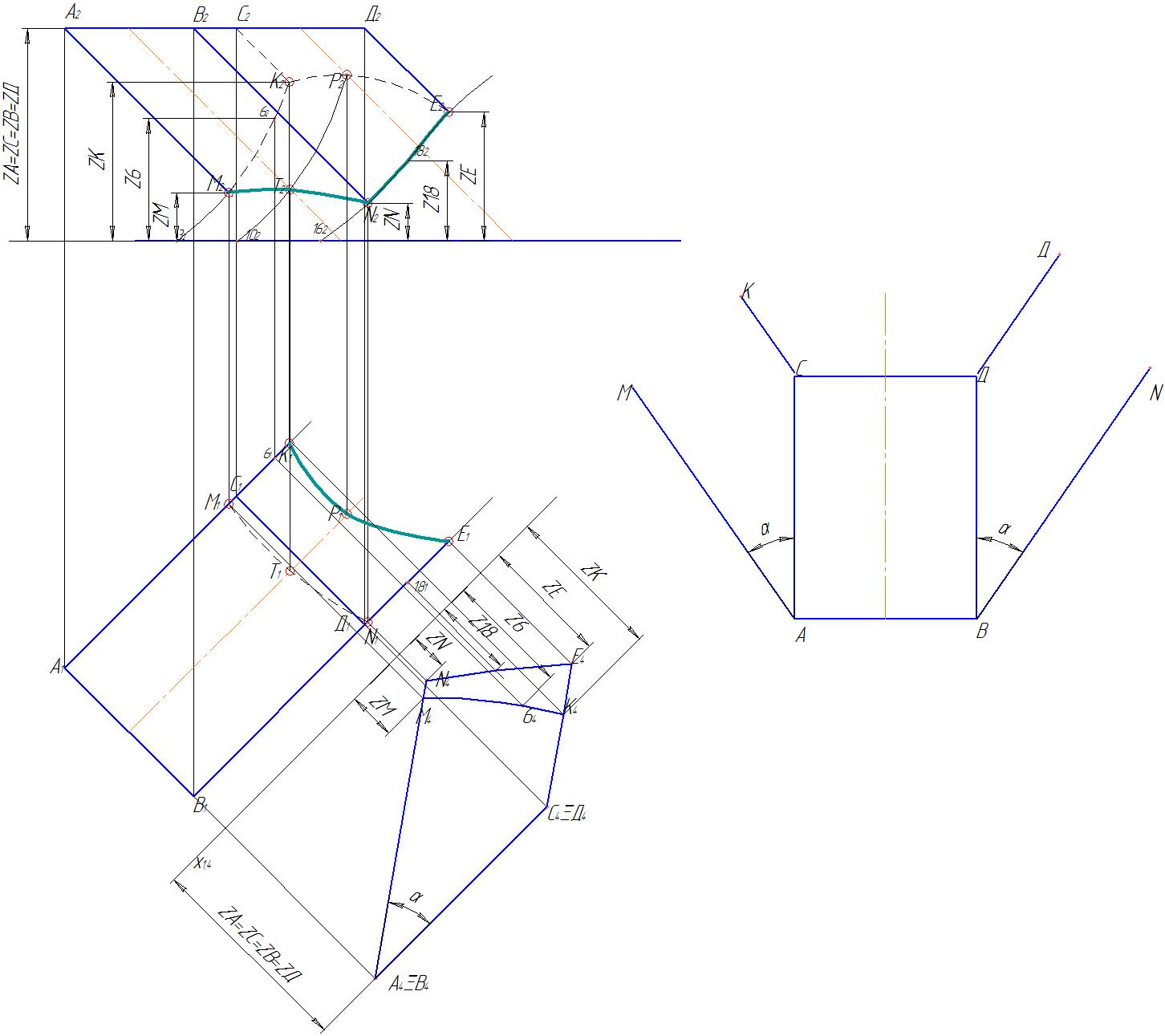
Рис. 69. Последовательность выполнения развертки призмы

Чтобы построить кривизну линий сечения МК и DN используем координаты точек 6 и 18 (рис. 70). Две оставшиеся грани строим, используя уже имеющиеся ребра АМ, ВN, СК и DЕ. Кривизну линий сечения КЕ и МN строим, используя точки Т и Р.

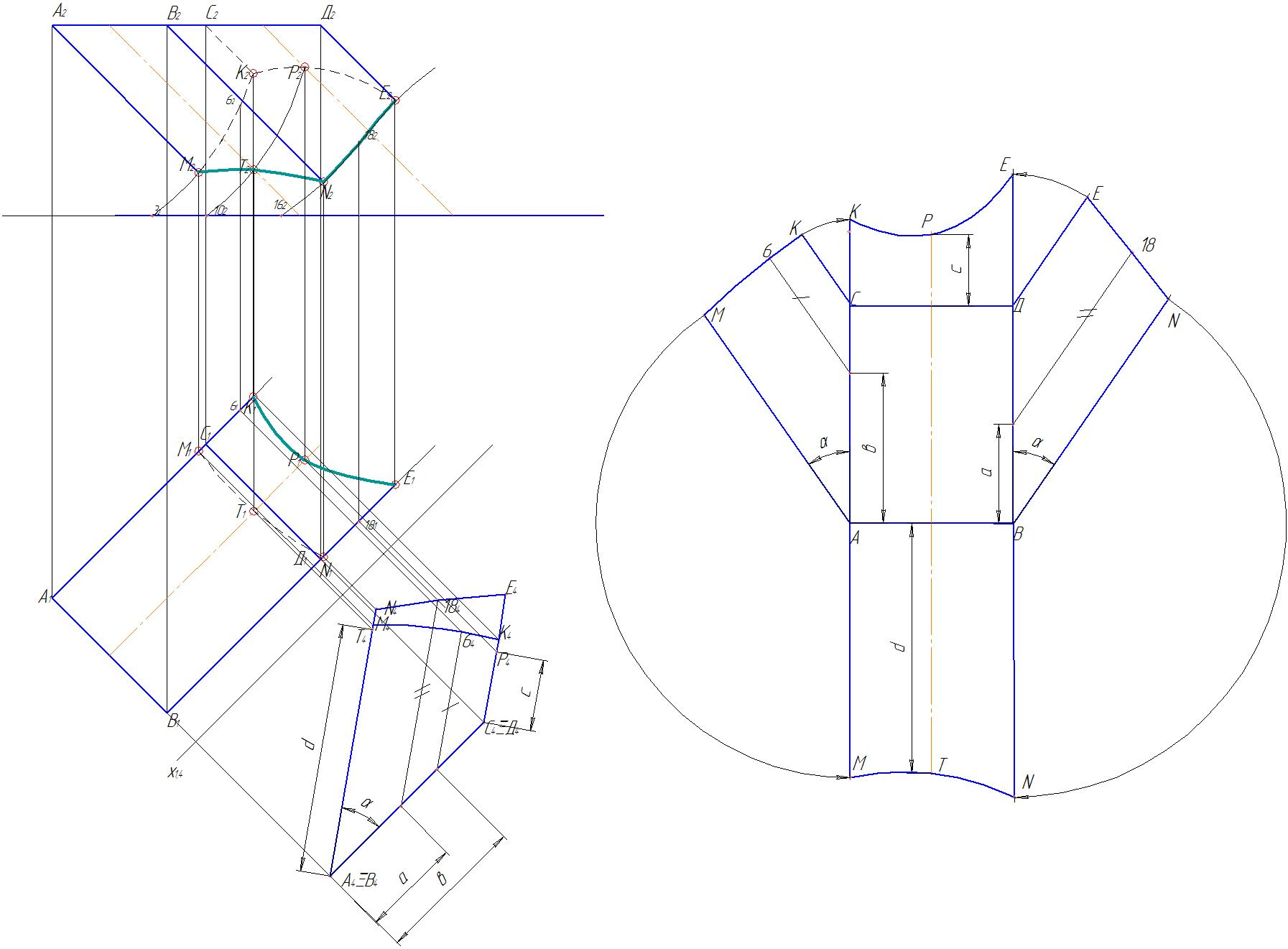
Рис. 70. Выполнение развертки призмы с линиями сечений

Линии АС, СD, DВ, ВА являются линиями сгиба, поэтому их выполняют штрихпунктирной линией с двумя штрихами (рис. 71).

Рис. 71. Развертка усеченной части призмы

Рис. 72. Образец выполнения эпюра 3. Построение линий пересечения поверхностей

Рис. 73. Образец выполнения эпюра 3. Нахождение натуральной величины граней призмы

Рис. 74. Образец выполнения эпюра 3. Построение развертки усеченной части призмы

Эпюр 4. Геометрическое формообразование поверхностей

Содержание эпюра

Д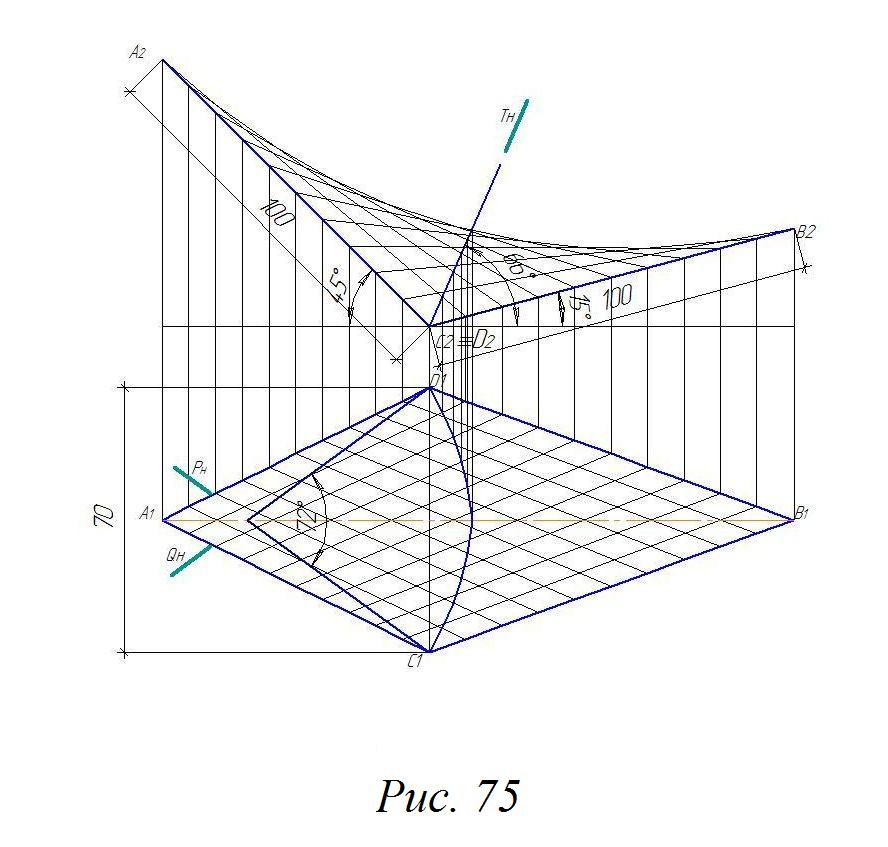ано: гиперболический параболоид и секущие плоскости (рис. 75).

Рис. 75. Чертеж к эпюру 4

Требуется:

1. Построить план и фасад составной поверхности из заданного количества отсеков, полученных с помощью трех секущих плоскостей из гиперболического параболоида.

2. Построить аксонометрию (прямоугольную диметрию).

3. Выполнить макет составной поверхности.

Указания к выполнению эпюра. Данные для выполнения эпюра взять в соответствии с вариантом.

Варианты заданий к эпюру 4

(вариант выбирается по последней цифре зачетной книжки)

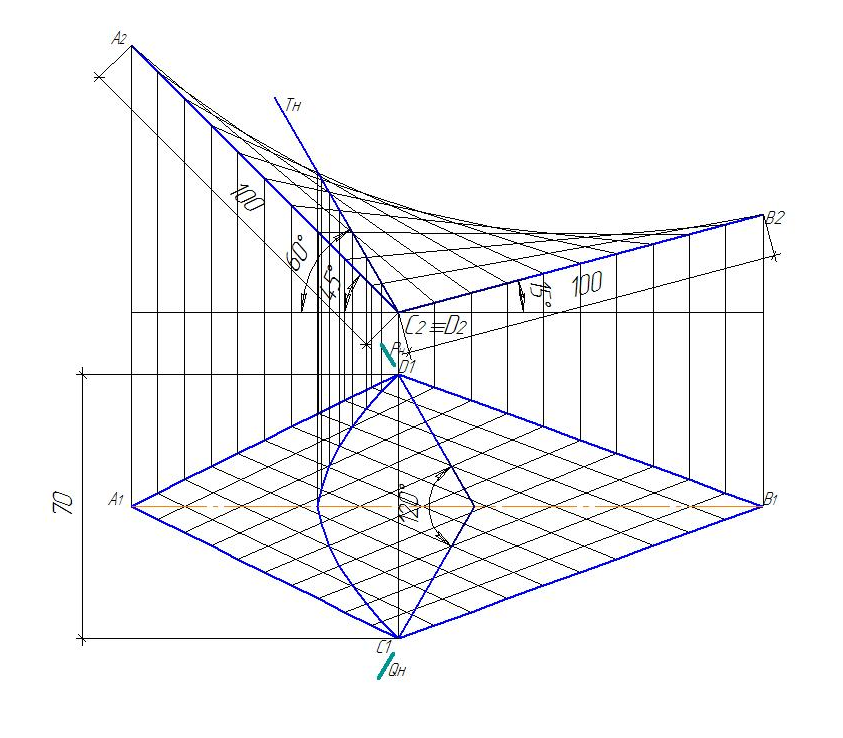
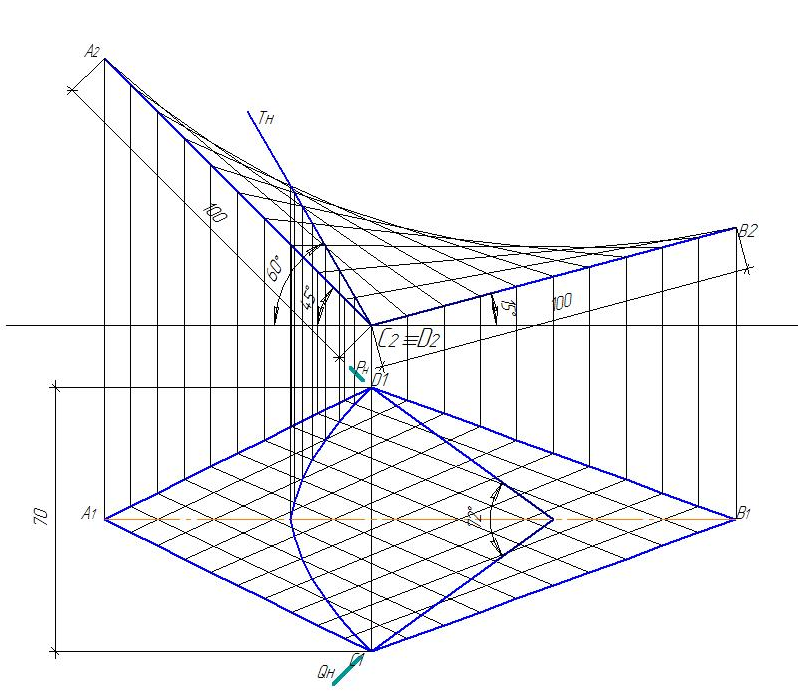
Вариант № 0

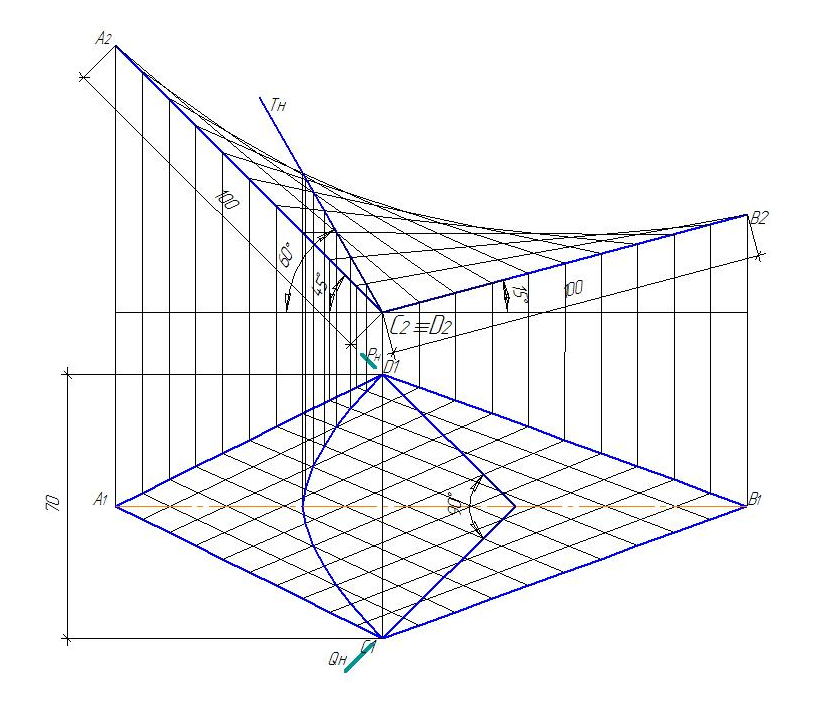
Вариант № 1

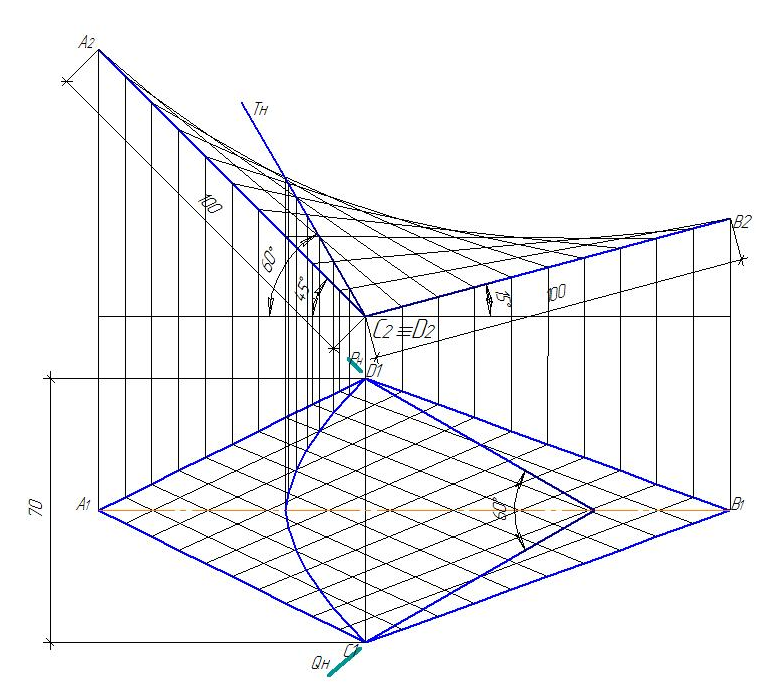
Вариант № 2

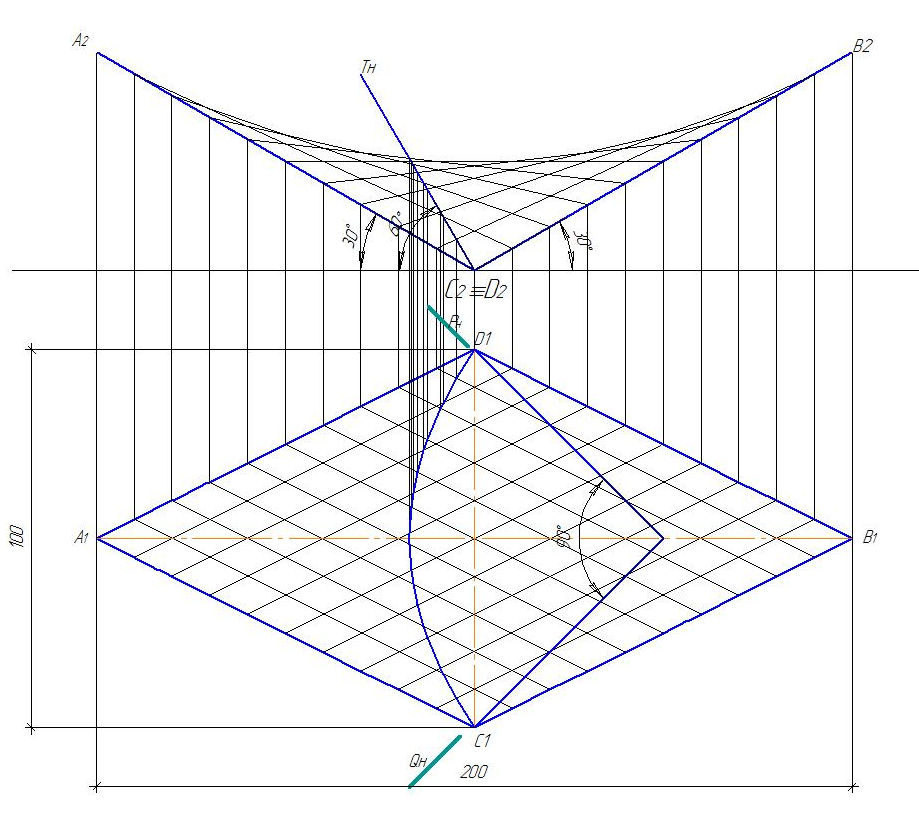
Вариант № 3

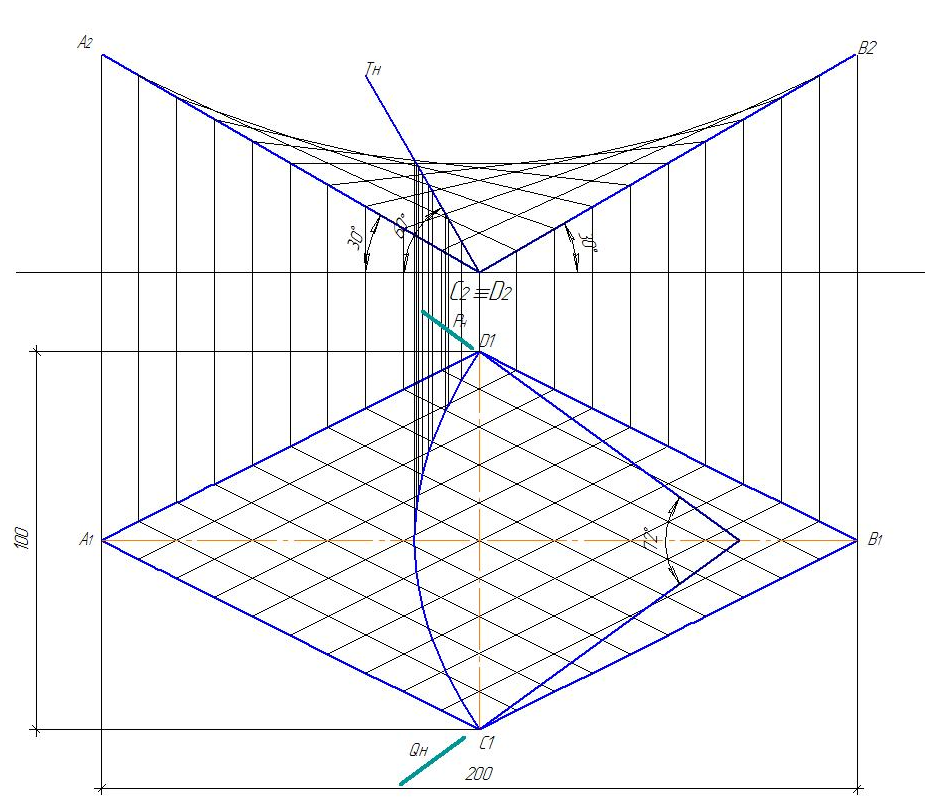
Вариант № 4

Вариант № 5

Вариант № 6

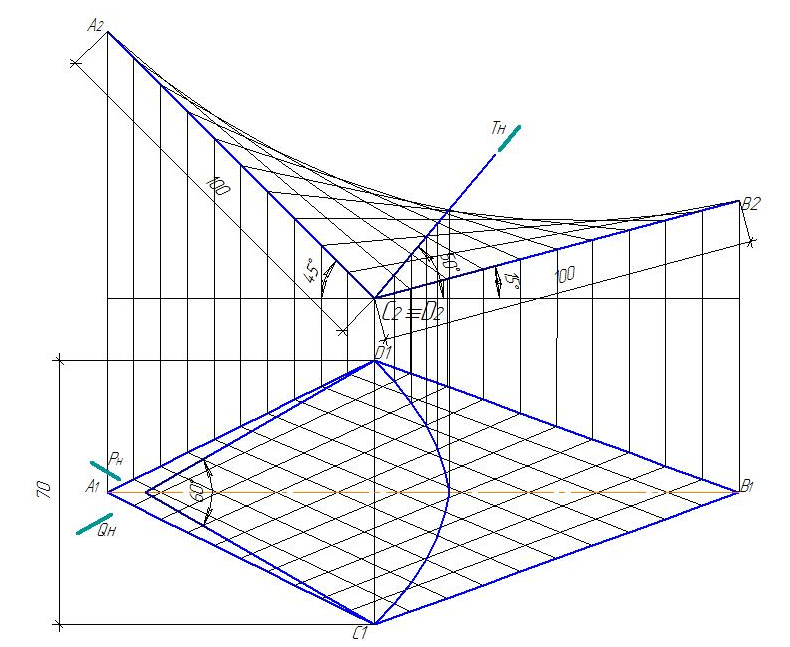
Вариант № 7

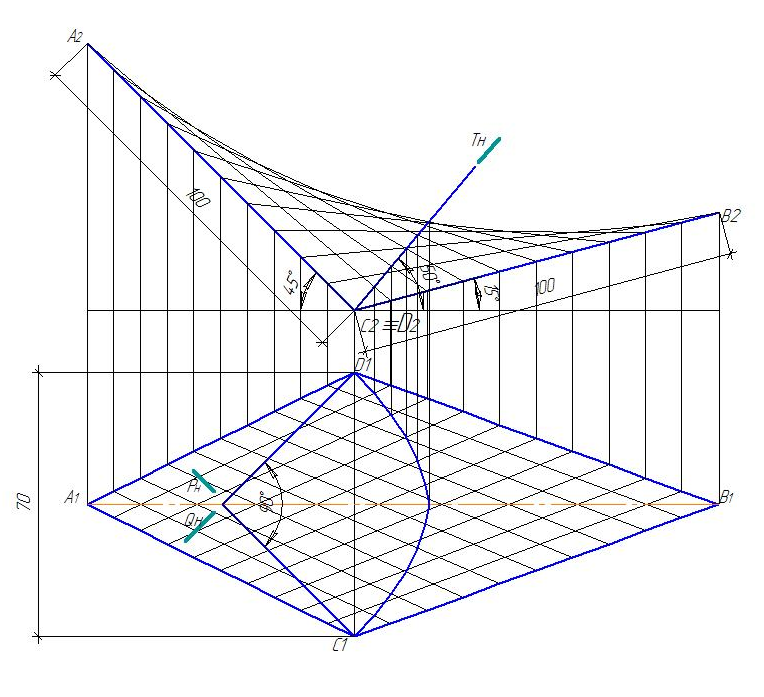
Вариант № 8

Вариант № 9

Образец выполнения эпюра представлен на рисунках 82 и 83.

Пояснения к выполнению эпюра 4

Задача 1

Построить план и фасад составной поверхности из заданного количества отсеков, полученных с помощью трех секущих плоскостей из гиперболического параболоида.

Этап 1 (рис. 76). Найдем точки пересечения горизонтально-проецирующих плоскостей Рн и Qн линиями построения гиперболического параболоида на горизонтальной проекции – это точки К1, 11, 21, 31... 71. По проекционным линиям найдем фронтальные проекции данных точек на соответствующих прямых. Соединим полученные точки К2, 12, 22, 32... 72 плавной кривой линией. Мы получили один отсек составной поверхности. Рассчитаем количество отсеков исходя из заданного угла между секущими плоскостями Рн и Qн. Он равен 72, значит 360: 72=5. Составная поверхность будет состоять из пяти одинаковых отсеков.

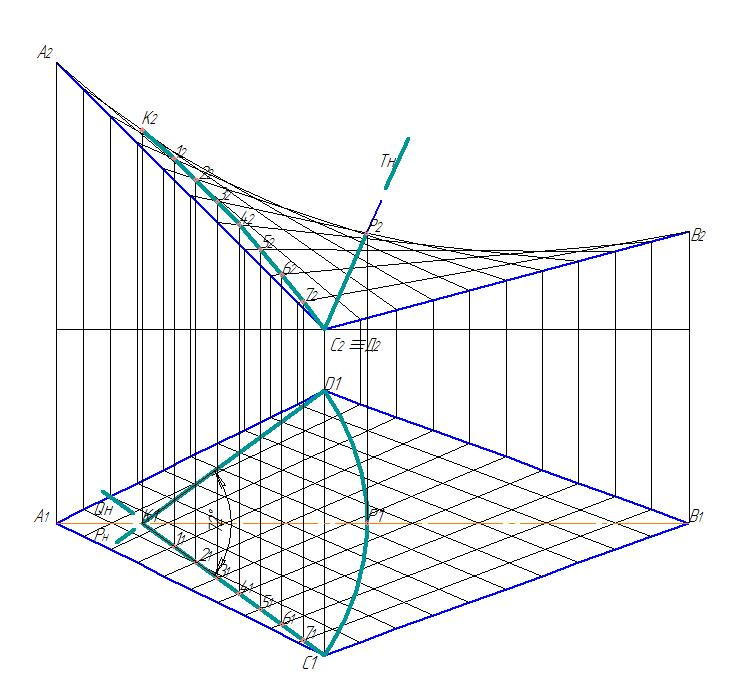
Рис. 76. Построение фронтальной проекции отсека, полученного с помощью трех секущих плоскостей из гиперболического параболоида

Этап 2 (рис. 77). Построим план и фасад составной поверхности. Начинаем построение с горизонтальной проекции (плана). Используя размеры полученного отсека, составляем полную поверхность из пяти отсеков. Переносим на горизонтальную проекцию составной поверхности использованные нами точки К1, 11, 21, 31... 71, проводим через них окружности, чтобы эти точки можно было найти на любом отсеке. Для точности построения арки С2Р2 D2 используем дополнительные точки 8 и 8. Данные точки мы задаем на горизонтальной проекции, а потом находим их фронтальные проекции. Для точности построения кривизны срединной части отсека (Р2 К2) мы берем произвольные дополнительные точки М2 и Е2 и находим их горизонтальные проекции.

Используя высоты точек К2, 12, 22, 32... 72, точек 82 и 82, точек М2 и Е2, строим на фронтальной проекции сначала первый отсек, а затем остальные.

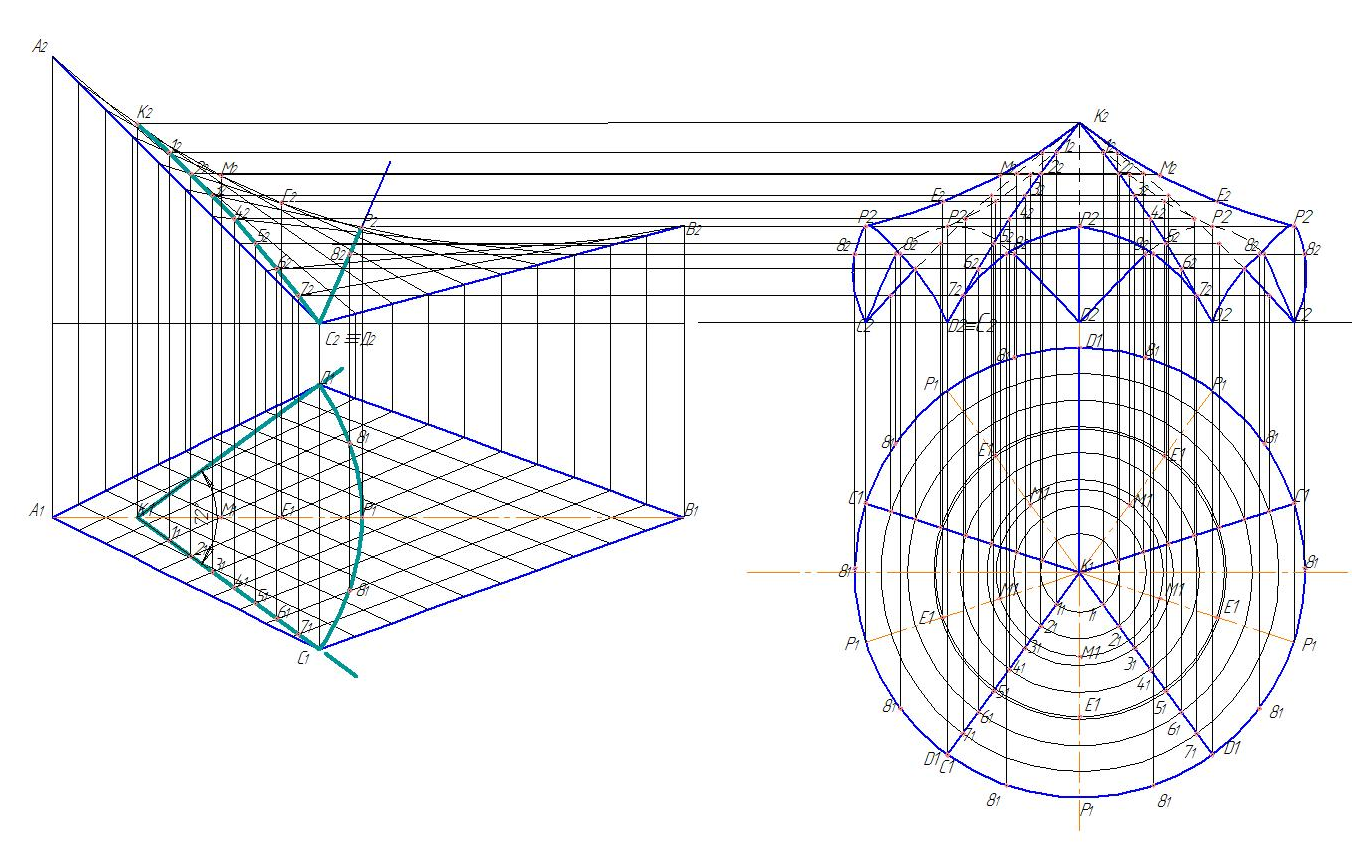
Рис. 77. Построение плана и фасада составной поверхности