Задача 72
Построить линию пересечения двух поверхностей вращения (рис. 182).
Задача 73
Построить линию пересечения двух конусов (рис. 183).
Задача 74
Построить линию пересечения конуса и полусферы (рис. 184).
Задача 75
Построить линию пересечения сферы и конуса (рис. 185).
|
|
|
|
Рис. 182
|
Рис. 183
|
|
|
|
|
Рис. 184 |
Рис. 185 |
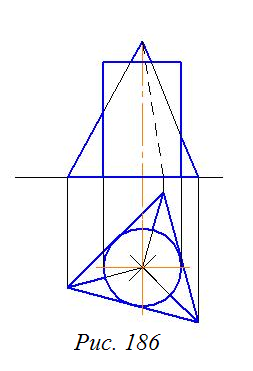
Задача 76
Построить линию пересечения пирамиды и цилиндра (рис. 186).
Решение. Проведем секущие плоскости через ребра пирамиды и еще несколько произвольных (рис. 187). Используя горизонтальные проекции данных секущих плоскостей, найдем фронтальные проекции точек сечения (горизонтальные проекции точек сечения лежат на проекции цилиндра). Горизонтальная проекция основания пирамиды имеет точки касания с горизонтальной проекцией цилиндра (21, 31, 41). Данные точки являются начальными точками линии сечения. Наивысшие точки сечения можно получить, проведя через ребра пирамиды секущие плоскости.
|
|
|
|
Рис. 186 |
Рис. 187. Построение линии пересечения цилиндра и пирамиды |
Задача 77
Построить линию пересечения конуса и призмы (рис. 188).
Задача 78
Построить линию пересечения конуса и шестигранной призмы (рис. 189).
-
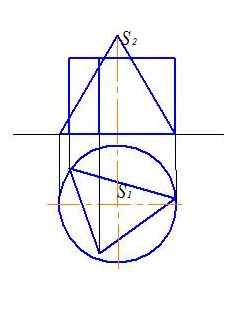
Рис. 188
Рис. 189
Задача 79
Построить линию пересечения полусферы с шестигранной призмой (рис. 190).
Задача 80
Построить линию пересечения пирамиды и цилиндра (рис. 191).
|
|
|
|
Рис. 190 |
Рис. 191 |
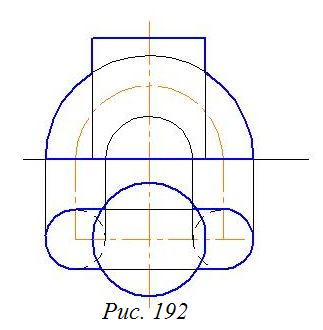
Задача 81
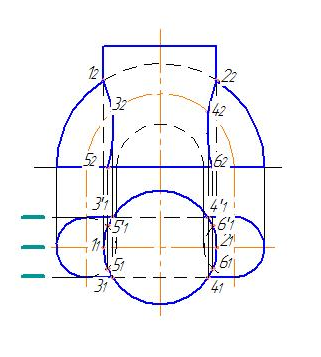
Построить линию пересечения полутора и цилиндра (рис. 192).
|
|
|
|
Рис. 192
|
Рис. 193. Построение линии пересечения полутора с цилиндром |
Решение. Введем три секущие горизонтально-проецирующие плоскости через проекцию полутора (рис. 193). Найдем горизонтальные точки пересечения данных секущих плоскостей с проекцией цилиндра (11, 21, 31, 31, 41, 41, 51, 51, 61, 61). Построим фронтальные проекции данных точек сечения и соединим их плавной кривой линией.
Задача 82
Построить линию пересечения конуса и цилиндра (рис. 194).
Задача 83
Построить линию пересечения полутора и цилиндра (рис. 195).
-
Рис. 194
Рис. 195
Задача 84
Построить линию пересечения цилиндра и сферы (рис. 196).
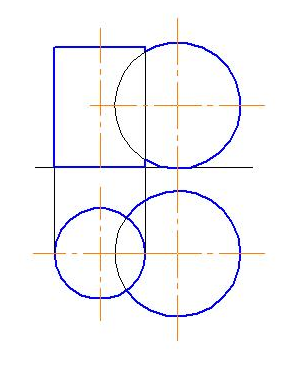
Рис. 196
Заключение
Архитектору в его профессиональной деятельности необходимо знание основ начертательной геометрии, так как выполнение архитектурных чертежей тесно связано с ортогональным черчением, построением аксонометрических и перспективных изображений, собственных и падающих теней зданий и сооружений.
Для архитекторов особое значение приобретают два раздела начертательной геометрии. Первый – раздел ортогональных проекций, рассматривающий теоретические принципы метода, которым выполняются основные чертежи, представляющие проект. Второй раздел – перспектива и тени, задача которого заключается в том, чтобы показать, как объект будет выглядеть в натуре после его возведения.
Данное пособие дает возможность приобрести знания по первому разделу. Изучив теоретическую основу различных методов построения, закрепив ее практическим выполнением упражнений, студенты приобретают знания, умения и навыки, необходимые не только для успешной сдачи экзамена по начертательной геометрии, но и для освоения профилирующей дисциплины – архитектурного проектирования.