Задача 20

Через точку В провести прямую, параллельную данной прямой а. Определить расстояние между параллельными прямыми (рис. 117).

Задача 21

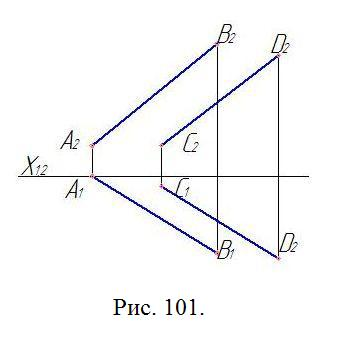
Построить линию, лежащую на одинаковом расстоянии от отрезков АВ и СD (рис. 118).

Рис. 117	Рис. 118

Задача 22

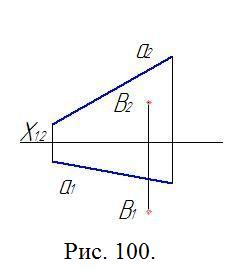
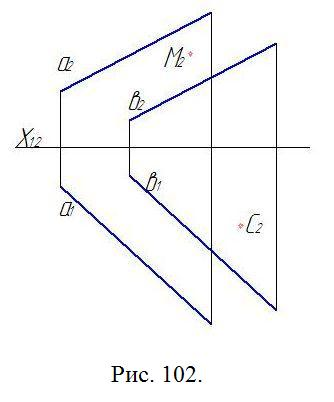
Найти натуральную величину отрезка СМ, принадлежащего плоскости, заданной двумя параллельными прямыми а и в (рис. 119).

Задача 23

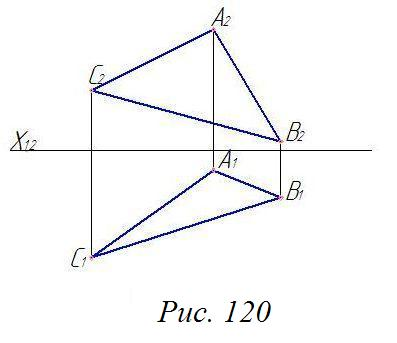
Определить истинную величину треугольника АВС и угол его наклона к плоскости П1 (рис. 120).

Рис. 119	Рис. 120

Решение. Построим горизонталь (h) на проекциях треугольника АВС (рис. 121). К горизонтальной проекции горизонтали (h1) введем перпендикулярную ей плоскость П4. Найдем новые проекции вершин треугольника (А4, В4, С4), используя высоты их фронтальных проекций. Соединим полученные точки. Если все сделали правильно, они расположатся на одной прямой (плоскость превратилась в прямую линию, значит, она стала фронтально-проецирующей). Введем новую плоскость, параллельную полученной проекции плоскости А4 В4 С4, – П5. Опустим на нее проекционные связи и, используя расстояния от оси Х1,4 до проекций точек А1, В1, С1, получим новые проекции А5 В5 С5. Соединив точки отрезками, получим треугольник, который является натуральной величиной треугольника АВС.

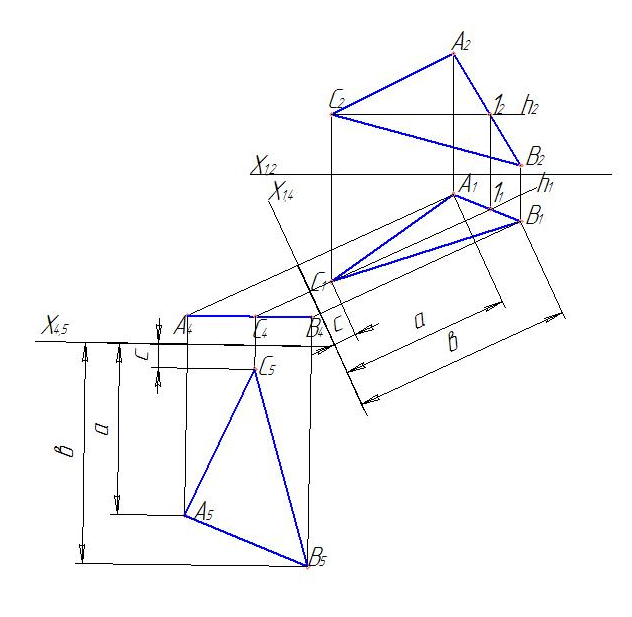
Рис. 121. Нахождение натуральной величины треугольника АВС

Задача 24

Способом замены плоскостей определить истинную величину треугольника АВС (рис. 122).

Задача 25

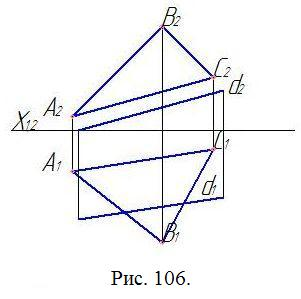
Определить расстояние между плоскостью АВС и параллельной ей прямой d (рис. 123).

Рис. 122	Рис. 123

Задача 26

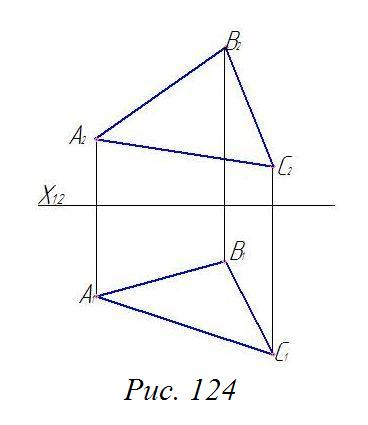
Построить плоскость, параллельную данной плоскости АВС, на расстоянии 40 мм (рис. 124).

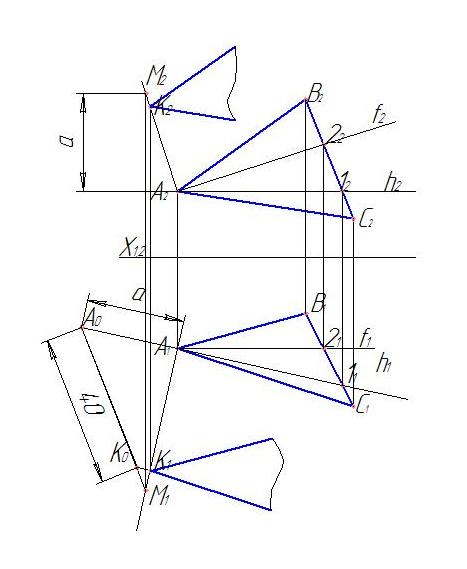
Рис. 124	Рис. 125. Построение плоскости, параллельной данной АВС, на расстоянии 40 мм

Решение. Проведем фронталь и горизонталь в плоскости АВС (рис. 125). Перпендикулярно фронтали (f2) восстановим из вершины А2 отрезок произвольной величины. Перпендикулярно горизонтали (h1) из точки А1 проведем отрезок произвольной величины. Отметим на отрезке из точки А2 произвольную точку М2 и найдем ее горизонтальную проекцию по проекционной связи. Определим натуральную величину отрезка АМ с помощью способа прямоугольного треугольника. На натуральной величине А0М1 откладываем от точки А0 40 мм и отмечаем точку К0. Проекцию точки К1 находим методом подобия, проведя из точки К0 прямую, параллельную А1А0 до пересечения с А1М1. Плоскость, параллельную данной плоскости АВС, можно задать двумя пересекающимися прямыми, используя признак параллельности.

Задача 27

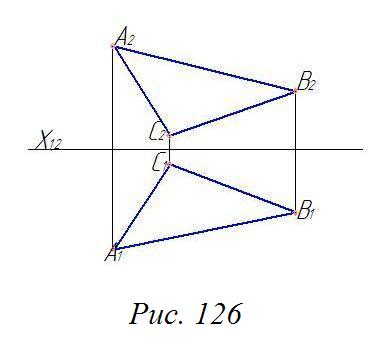
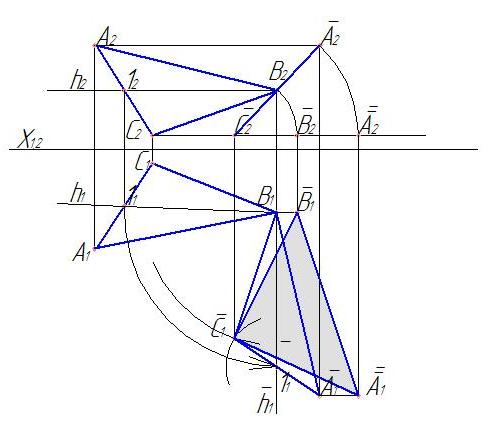
Определить истинную величину треугольника АВС способом вращения горизонтали (рис. 126).

Решение. Проведем фронтальную проекцию горизонтали из точки В2 (h2) и найдем по проекционной связи ее горизонтальную проекцию (h1) (рис. 127). С помощью вращения вокруг точки В1 горизонталь (h1) примет вертикальное положение. На ней отметим точку ī1 и относительно этой точки построим новое положение горизонтальной проекции треугольника (Ā1В1Ć1). Найдем фронтальные проекции полученных точек Ā1, В1, Ć1. Это точки Ā2, В2, Ć2. Проекции выстроились в линию, следовательно, плоскость АВС стала фронтально-проецирующей. Повернем проекцию Ā2В2Ć2 относительно точки Ć2 до горизонтального положения, получим новые проекции точек. Найдем их горизонтальные проекции с помощью проекционных связей. Полученный треугольник является истинной величиной треугольника АВС.

Рис. 126	Рис. 127. Нахождение истинной величины треугольника АВС помощью вращения горизонтали