• Тема 10. Статистичні методи вивчення взаємозв’язків явищ

План вивчення теми

1. Сутність та види взаємозв’язків явищ. Графічні методи вивчення кореляційного зв’язку

2. Метод аналітичних групувань і дисперсійний аналіз. Оцінювання щільності кореляційного зв’язку за даними аналітичного групування

3. Регресійно-кореляційний аналіз взаємозв’язку. Оцінювання щільності та перевірка істотності кореляційного зв’язку на основі рівняння регресії

Після вивчення теми студенти повинні:

• знати: суть і види взаємозв’язків явищ; аналітичні можливості й передумови використання методу аналітичних групувань й дисперсійного аналізу, оцінювання щільності та перевірки істотності кореляційного зв’язку на основі рівняння регресії;

• уміти: обґрунтовано використовувати на практиці різні методи аналізу взаємозв’язків між явищами відповідно до мети дослідження і наявної інформації.

Бібліографічний список: [7 – 10; 17 - 22 ]

1. Сутність та види взаємозв’язків явищ. Графічні методи вивчення кореляційного зв’язку

Закономірності економічних та соціальних процесів характеризуються взаємозв’язками між статистичними показниками. Статистичні показники перебувають у певних відношеннях між собою, виступаючи в ролі незалежних або залежних ознак, між якими існує причинно – наслідковий характер.

Суспільні явища, що впливають на інші явища, називають факторними, їх характеризують факторні ознаки (х). Явища, які змінюються під впливом факторних явищ, називаються результативними, їх характеризують результативні ознаки (у).

Між явищами може існувати функціональний, стохастичний або кореляційний зв'язок. Функціональний зв'язок між явищами характеризується повною відповідністю між причиною і наслідком, факторною і результативною ознакою, тобто за цього зв'язку кожному можливому значенню факторної ознаки х відповідає чітко визначене значення результативної ознаки у. Такі зв'язки найчастіше зустрічаються у фізичних, хімічних явищах.

Стохастичний зв'язок виявляється зміною умовних розподілів, тобто за цього зв'язку кожному значенню ознаки х відповідає певна множина значень ознаки у, які варіюють і утворюють так званий умовний розподіл.

Якщо замінити умовний розподіл середньою величиною ,то утвориться різновид стохастичного зв’язку – кореляційний, при якому кожному значенню ознаки х відповідає середнє значення результативної ознаки (які обчислюються як середня арифметична зважена):

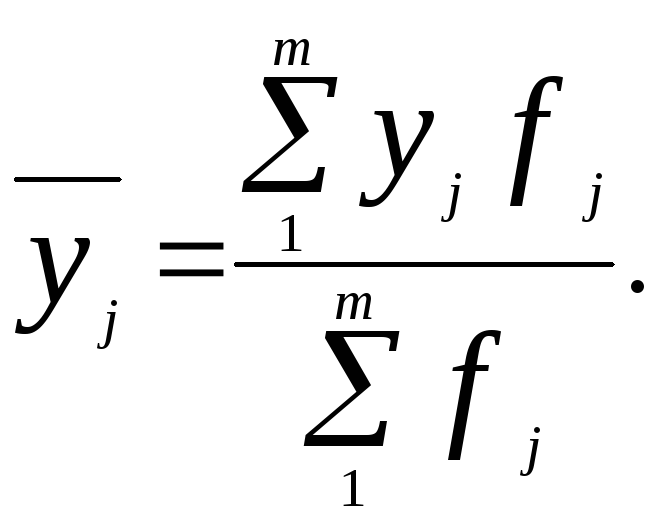
Поступова зміна середніх _j від однієї групи до іншої свідчить про наявність кореляційного зв'язку між ознаками. За кореляційного зв'язку, на відміну від функціонального, звичайно немає відомостей про повний перелік усіх ознак-факторів, які впливають на результативну ознаку, а також про точний механізм їх взаємодії з ним у вигляді тієї чи іншої математичної формули, функції.

Функціональні зв'язки виражаються тим чи іншим аналітичним рівнянням, кореляційні зв'язки можуть бути виражені за допомогою аналітичного рівняння лише приблизно.

Якщо залежність результативної ознаки від певної ознаки-фактора може бути виражена рівнянням прямої лінії, то зв'язок називається прямолінійним (лінійним), якщо ж залежність виражається рівнянням якої-небудь кривої (гіперболи, параболи та ін.), то зв'язок називається криволінійним.

Якщо досліджується залежність результативної ознаки тільки від однієї ознаки-фактора, то зв'язок називається однофакторним. Якщо при цьому зв'язок є функціональним, то це свідчить про те, що результативна ознака залежить тільки від певної ознаки. Якщо ж зв'язок є кореляційним, то включення в аналітичне рівняння тільки одного фактора свідчить про те, що від впливу інших факторів ми абстрагуємося, усуваємо їхню дію. Така кореляція називається парною, оскільки при цьому розглядаються тільки дві ознаки.

На відміну від функціональної залежності, кореляційний зв’язок є неповним, тому що залежність між функцією і аргументом у кожній ситуації перебуває під впливом ще й інших факторів. Кореляційна залежність проявляється тільки у масових явищах і може встановлюватися для пари показників (парна кореляція) або для декількох показників (множинна кореляція).

Лінія регресії може мати різні зображення: табличне, аналітичне та графічне. Як правило, графіки мають другорядне, переважно ілюстративне, значення, хоча на етапі теоретичного обґрунтування моделі значно спрощують її вибір.

Одним з найпростіших і наочних прийомів виявлення кореляційної залежності між двома ознаками та оцінки її характеру за незгрупованими даними є графічна побудова так званого кореляційного поля та подальший аналіз його виду.

Для цього у системі координат за віссю абсцис розташовується значення одного показника, а за віссю ординат – іншого. Якщо точки розкидані по полю досить рівномірно, то це свідчить про відсутність зв’язку між показниками (рис. 10.1).

Проте не завжди вигляд кореляційного поля допомагає визначитися з видом залежності між ознаками. Тоді використовують перебір функцій, тобто обчислюють рівняння регресії різних видів, а потім з них обирають найкраще. Як правило, це рівняння має найбільший коефіцієнт щільності зв’язку між ознаками, що вивчаються.

Y

* * * * *

* * * * * * *

* * * * * *

* * * * *

* * * * *

* * * * *

Х

Рис. 10.1. Кореляційне поле ознак Х таY

Якщо існує певна залежність між ознаками, на це покаже скупчення точок (рис. 10.2).

Y

* * * * *

* * * * * *

* * * * *

* * * * *

* * * * *

* * * *

* * *

* *

Х

Рис. 10.2. Кореляційне поле ознак Х таY

Характеристикою кореляційного зв’язку є лінія регресії, яка розглядається у двох моделях: аналітичного групування та регресійного аналізу.

2. Метод аналітичних групувань і дисперсійний аналіз. Оцінювання щільності кореляційного зв’язку за даними аналітичного групування

Виявлення кореляційного зв’язку за допомогою аналітичного групування проводиться за такими етапами:

1. Теоретичне обґрунтування моделі аналітичного групування:

- вибір факторних ознак;

- визначення числа груп k ознаки-фактора x_i;

- визначення меж інтервалів групування щодо x_i.

Примітка. Групи мають бути достатньо чисельні й чисельність груп має бути приблизно однакова.