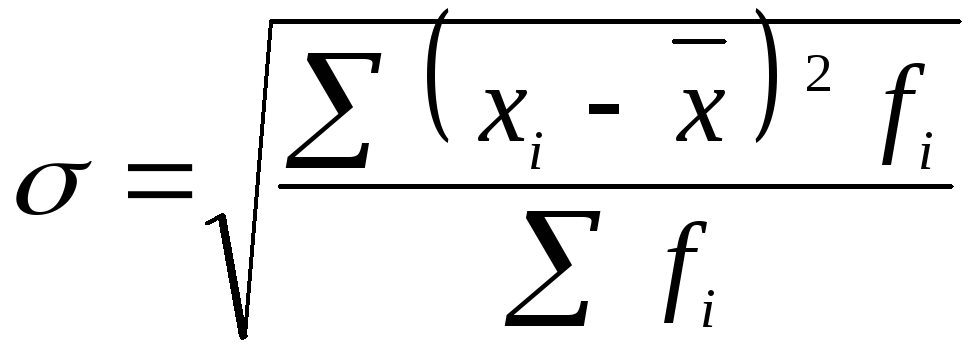Показники варіації та формули для їх розрахунку

Назва показника	Розрахункова формула за даними
	не згрупованими	згрупованими
Середнє лінійне відхилення
Середнє квадратичне відхилення
Дисперсія
хі – індивідуальні значення окремої ознаки, варіанти –середня арифметична (середнє значення ознаки) n – обсяг сукупності, кількість ознак у сукупності fi – частота відповідної ознаки.

Дисперсія являє собою середній квадрат відхилень, є відповідні властивості дисперсії і вона пов’язана з середнім квадратичним відхиленням таким співвідношенням:

,

де  – середнє квадратичне відхилення

D =  ² – дисперсія.

При порівнянні варіації різних ознак або однієї ознаки у різних сукупностях використовуються відносні характеристики: коефіцієнти варіації. До них належать:

• лінійний коефіцієнт варіації, який обчислюється за формулою:

, або ·100 %,

де – середнє лінійне відхилення

–середня арифметична;

• квадратичний коефіцієнт варіації, який обчислюється за формулою:

, або ·100 %,

де  – середнє квадратичне відхилення

• коефіцієнт осциляції, який обчислюється за формулою:

,

де R – розмах варіації.

Чим менше середнє відхилення, тим більш типова середня, тим більш однорідна сукупність. Найчастіше квадратичний коефіцієнт варіації використовують як критерій однорідності сукупності, він є ознакою надійності середньої.. У симетричному, близькому до нормального, розподілі V_σ = 0,33.

Для малих сукупностей розрізняють такі значення відносних коливань:

V_σ < 10% - незначне коливання, сукупність однорідна, значення середньої є типовим рівнем ознаки в даній сукупності;

10 % ≤ V_σ ≤ 33% - середнє коливання, сукупність в межах однорідності, значення середньої можна вважати типовим рівнем ознаки в даній сукупності;

V_σ > 33% - високий рівень варіації, сукупність неоднорідна, значення середньої неможна вважати типовим рівнем ознаки в даній сукупності.

Дисперсія альтернативної ознаки обчислюється як добуток часток за формулою:

,

де d ₁ – частка елементів сукупності, яким властива ознака

d ₀ – частка решти елементів, у яких відсутня ознака (d ₀ = 1 – d ₁).

Дисперсія альтернативної ознаки широко використовується під час проектування вибіркових обстежень, обробці даних соціологічних опитувань, статистичному контролі якості продукції тощо.

3. Характеристики форми розподілу: коефіцієнти асиметрії та ексцесу

Різноманітність статистичних сукупностей – передумова різних форм співвідношення частот і значень варіативної ознаки. За своєю формою роз-поділи поділяються на одновершинні (див. рис. 6.7) та багатовершинні (коли розподіл має дві, три та більше вершин). Наявність двох і більше вершин (див. рис. 6.8) свідчить про неоднорідність сукупності, про поєднання в ній груп з різними рівнями ознаки. У такому разі необхідно більш ретельно проаналізувати наявну вихідну інформацію, перегрупувати дані, виділивши однорідні групи. Розподіли якісно однорідних сукупностей, як правило, одновершинні. Серед одновершинних розподілів є симетричні та асиметричні (скошені), гостровершинні та плосковершинні.

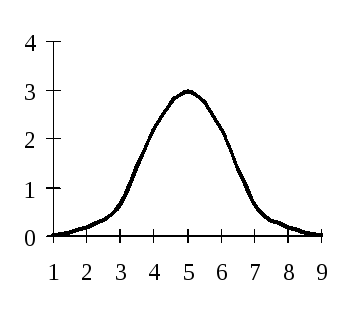
Рис.6.7. Одновершинний розподіл Рис. 6.8. Багатовершинний розподіл

У симетричному розподілі рівновіддалені від центра значення ознаки мають однакові частоти, при цьому середня, мода та медіана мають однакові значення = Мо = Ме в асиметричному – вершина розподілу зміщена. Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена вліво, то це правостороння асиметрія. У цьому випадку > Me > Mo. Якщо вершина зміщена вправо, то це лівостороння асиметрія. В цьому випадку< Me < Mo. Асиметрія (див. рис. 6.9) виникає внаслідок обмеженої варіації в одному напрямі або під впливом домінуючої причини розвитку, яка веде до зміщення центру розподілу. Очевидно, що в симетричному розподілі А = 0, при правосторонній асиметрії A > 0, при лівосторонній – A < 0.

Найпростішою мірою асиметрії є відхилення від середньої арифметичної медіани чи моди. В симетричному розподілі характеристики центра мають однакові значення = Мо = Ме в асиметричному – між ними існують певні розбіжності.

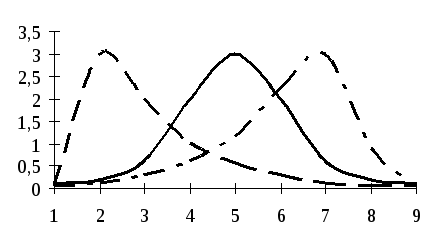
Рис. 6.9. Види розподілу:

-симетричний розподіл (Мо = Ме = );

-правостороння(додатня ) асиметрія (Мо < Ме < );

• -лівостороння (від’ємна) асиметрія (Мо > Ме >).

Стандартизовані відхилення, які мають назву коефіцієнта асиметрії, характеризують напрям та міру скошеності розподілу і розраховуються за формулами:

або .;

Якщо має місце відхилення коефіцієнта асиметрії від нуля в той чи інший бік, то можна вести мову про більшу чи меншу асиметрію. Вважають, що при 0,25 асиметрія низька при 0,25<0,5 - помірна, або середня при >0,5 - асиметрія висока.

Характеристики центру розподілу ґрунтуються на моментах розподілу. Момент розподілу – це середня k-го ступеня відхилень . Залежно від величиниа моменти поділяють на первинні (а = 0), центральні і умовні(a = const). Ступінь k визначає порядок моменту. В загальному вигляді центральний момент k-го порядку розраховується за формулою:

,

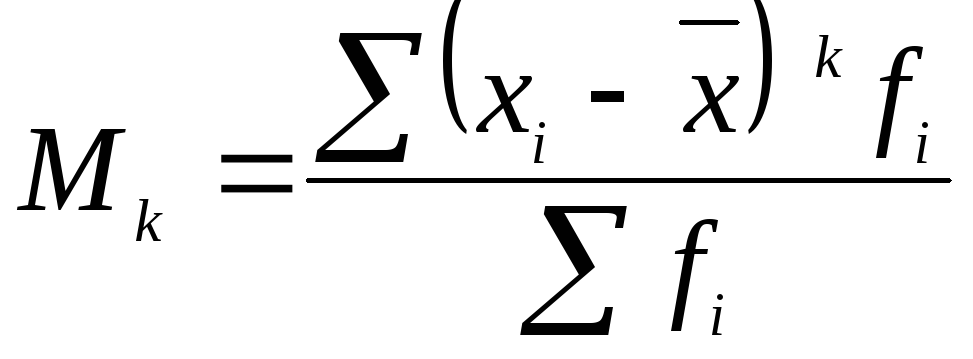де х_і – значення окремої варіанти;

–середня арифметична;

k – ступінь моменту;

f_i – частота окремої варіанти.

Для того, щоб характеристика скошеності не залежала від масштабу вимірювання ознаки для порівняння ступеня асиметрії різних розподілів, використовують стандартизований момент третього ступеня.В такому разі коефіцієнт асиметрії визначається за формулою:

,

де М₃ – центральний момент третього порядку;

–середнє квадратичне відхилення.

Гостровершинність розподілу відображає скупченість значень ознаки навколо середньої величини та називається ексцесом. Для вимірювання ексцесу використовують коефіцієнт, побудований за допомогою стандартизованого моменту четвертого порядку, який розраховується за формулою:

,

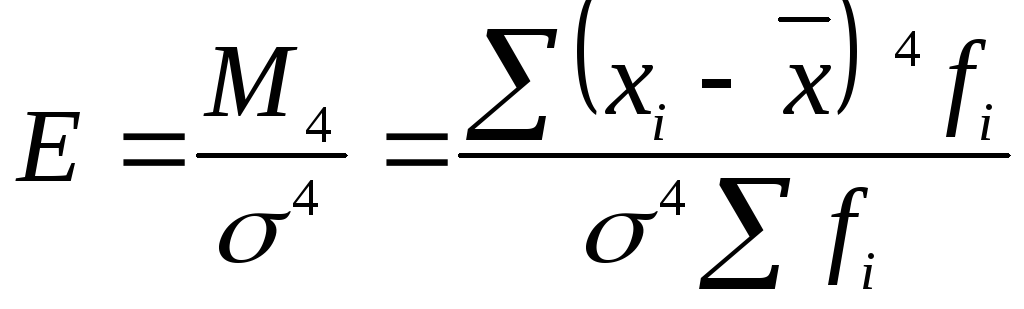де М₄ – центральний момент четвертого порядку.

Якщо Е = 3, то розподіл уважається нормальним, при E < 3 – плосковершинний, при E > 3 - розподіл має гостровершинну форму. Термін «ексцес» грецького походження (kurtosis), тому назви форми ексцесу походять від цього кореня слова (див. рис.6.10):

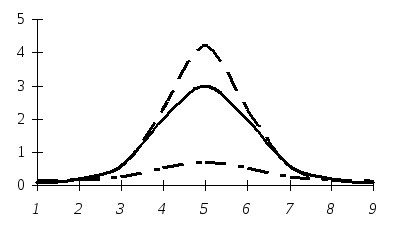
Рис.6.10. Види розподілу:

• нормальний (мезокуртичний) (Е = 3);

• гостровершинний (стрічкокуртичний) (Е > 3);

• плосковершинний (платокуртичний) (Е < 3).

Наведений графік свідчить, що для стрічкокуртичної кривої характерне розміщення більшості одиниць сукупності поблизу центра. У випадку платокуртичної кривої (форма силуету – плато) варіанти значно віддалені від центру розподілу. Помірне розміщення навколо центра розподілу варіант визначає форма ексцесу у вигляді мезокуртичної кривої. На практиці часто в одному розподілі поєднуються всі названі особливості, а саме: одновершинний розподіл може бути симетричним та гостровершинним, або плосковершинним з лівосторонньою асиметрією, або гостровершинним з правосторонньою асиметрією тощо.

3. Показники диференціації та концентрації

Процеси і явища в промисловому і сільськогосподарському виробництві, фінансовій та комерційній діяльності, демографічній, соціальній або політичній галузях, що вивчаються статистикою, як правило, характеризуються внутрішньою структурою, яка із часом може змінюватися. Динаміка структури викликає зміну внутрішнього змісту досліджуваних об’єктів і їх економічну інтерпретацію, приводить до змін встановлених причинно-наслідкових зв’язків. Тому вивчення структури і структурних зрушень займає дуже важливе місце в курсі статистики.

У статистиці під структурою розуміють сукупність одиниць, яким притаманна певна стійкість внутрішньо групових зв’язків при збереженні основних ознак, що характеризують цю сукупність як ціле.

Одним із найважливіших завдань держави є забезпечення сталого соціально-економічного розвитку на основі пропорційного співвідношення між окремими підсистемами. Тому останнім часом все більше уваги приділяється питанням теорії та практики аналізу пропорційності (або нерівномірності) розподілу як одного із напрямів обґрунтування взаємозв’язків розподілів, зокрема: ресурсів та їх використання; чисельності населення і споживання матеріальних благ і послуг; доходів і витрат; попитом і пропозицією та ін.

Практичний аналіз потребує дослідження і врахування у процесі управління пропорційності як двох взаємопов’язаних показників (результативної та факторної) ознак, так і однієї результативної оцінки з кількома факторними. За групову ознаку можуть при цьому слугувати окремі регіони, галузі, види діяльності, групи фізичних та юридичних осіб і т. ін.

Основні напрямки вивчення нерівномірності розподілу в різних соціально-економічних явищах:

• оцінка структури аналізованих сукупностей з використанням квантилів розподілу для виявлення різного рівня диференціації;

• визначення узагальнюючих характеристик концентрації та локалізації.

Мірою оцінки розшарування сукупності слугує коефіцієнт децильної диференціації. Коефіцієнт децильної диференціації, що є відношенням розмірів дев’ятого і першого дециля (наприклад, відношення мінімального середньодушового доходу 10% найбагатшого населення до максимального середньодушового доходу 10% найменш забезпеченого населення), дорівнює:

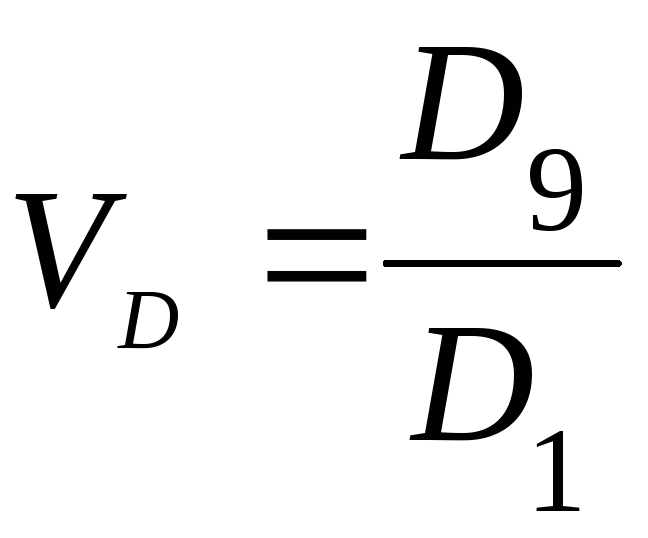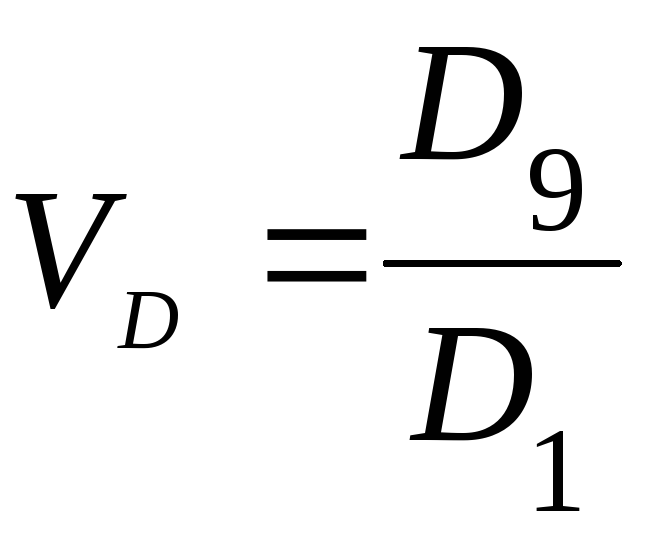, або ·100 %,

де D₉ – дев’ятий дециль

D₁ – перший дециль.

Але цей показник не зовсім точно вимірює рівень диференціації, так як співставляються, наприклад, мінімальна величина активів 10% самих великих банків із максимальною величиною активів 10% самих маленьких банків. Точніше рівень диференціації можна оцінити, співставляючи середні рівні активів 10% самих великих і 10% самих маленьких банків. Цей показник називають фондовим коефіцієнтом К_ф.

Ступінь нерівномірності розподілу досліджуваної ознаки, не пов’язаний ні з обсягом сукупності, ні з чисельністю окремих груп, називають концентрацією. При дослідженні нерівномірності розподілу досліджуваної ознаки за територією поняття “концентрація” замінюють поняттям “локалізація”. Централізація означає зосередженість (скупченість) обсягу ознаки у окремих одиниць (наприклад, капіталу в окремих комерційних банках, продукції якогось виду на окремих підприємствах і т. ін.).

Узагальнюючий показник централізації І_Z розраховується за формулою:

,

де m_i – значення ознаки і-ої одиниці сукупності ;

- обсяг ознаки всієї сукупності;

n - обсяг сукупності (кількість одиниць, що входять у сукупність).

Максимального значення І_Z досягає тільки за умови, що сукупність складається тільки із однієї одиниці, якій належить весь обсяг ознаки. Мінімальне значення цього показника наближається до нуля, але ніколи його не досягає.

Оцінка нерівномірності розподілу між окремими складовими сукупності ґрунтується на порівнянні часток двох розподілів – за кількістю елементів сукупності d_i і обсягом значень ознаки D_i.. Якщо розподіл значень ознаки рівномірний, то d_i = D_i, а відхилення часток свідчать про певну нерівномірність, яка вимірюється коефіцієнтами локалізації та концентрації.

Оцінювання інтенсивності структурних зрушень

Визначення структурних зрушень окремих частин сукупності та узагальнюючих характеристик структурних зрушень в цілому по сукупності базується на відносних показниках структури (див. лекцію до теми №4 "Узагальнюючі статистичні показники"), що являють собою співвідношення окремих частин і цілого. При цьому вони можуть бути представлені як частка (коефіцієнт) або питома вага (%). Як часткові, так і узагальнюючі показники структурних зрушень можуть відображати або “абсолютну” зміну структури у процентних пунктах чи долях одиниці, або її відносну зміну у процентах чи коефіцієнтах. “Абсолютна” зміна показана в лапках, тому що цей показник є абсолютним за методологією розрахунку, а не за суттю та одиницями виміру. До таких показників відносять:

• “абсолютний” приріст питомої ваги і - ої частини сукупності;

• темп зростання питомої ваги ( відносна зміна) і - ої частини сукупності;

• середній “абсолютний” приріст питомої ваги і - ої частини сукупності;

• середній темп зростання питомої ваги ( відносна зміна) і - ої частини сукупності за кілька періодів часу;

• лінійний і квадратичний коефіцієнти “абсолютних” структурних зрушень;

• квадратичний коефіцієнт відносних структурних зрушень;

• лінійний коефіцієнт “абсолютних” структурних зрушень за n періодів

За аналогією з коефіцієнтом концентрації при порівнянні структури одного об’єкта за двома ознаками або структур двох об’єктів розраховуютькоефіцієнт подібності (схожості) структур:

.

де d_j таd_k -питома вага (частка) відповідно j - ої таk - ої сукупності.

Якщо структури однакові, Р = 1. Чим більші відхилення структур, тим менше значення коефіцієнтаР.