• Тема 8. Виявлення і вимірювання тенденцій розвитку

План вивчення теми

1. Основні компоненти часових рядів. Основні методи виявлення та аналізу тенденцій розвитку

2. Рівняння тренду, етапи визначення та обґрунтування найпридатнішого функціонального виду, суть параметрів

3. Екстраполяція трендів як один із методів прогнозування рівнів соціально-економічних явищ

Після вивчення теми студенти повинні:

• знати: принципи виявлення та аналізу тенденції розвитку, екстраполяції трендів як методу прогнозування рівнів соціально-економічних явищ;

• уміти: обґрунтовано використовувати на практиці основні методи виявлення та аналізу тенденцій розвитку, прогнозувати розвиток шляхом екстраполяції тренду.

Бібліографічний список: [7 – 10; 17 - 22 ]

8.1. Основні компоненти часових рядів. Основні методи виявлення та аналізу тенденцій розвитку

Рівні ряду динаміки формуються під загальним впливом великої кількості факторів, дія яких може бути тривалою або короткочасною, вони можуть бути постійно діючими і випадковими, які з’являються під впливом різних обставин. Визначення основної закономірності зміни рівнів ряду у часі потребує її кількісного вираження, більш менш вільного від дії випадкових чинників.

Основна тенденція розвитку явища – це певний напрям його зміни, який характеризується детермінованою складовою ряду динаміки. Але крім впливу основних факторів, які і визначають конкретний вид невипадкової компоненти (тренд), на рівні ряду впливають випадкові фактори, що викликають відхилення фактичних значень рівнів ряду від тренда.

Рівень динамічного ряду можна представити функцією:

,

де f(t) – тенденція, зумовлена впливом постійно діючих факторів (тренд);

ε(t) – величина, що визначає вплив випадкових коливань.

Однак, існує багато явищ, яким, крім вище названих, притаманні ще й так звані сезонні коливання. Рівень таких явищ рік у рік у певні місяці підвищується, а в інші – знижується. Наприклад, витрати палива у весняно-літні місяці значно більші, ніж у осінньо-зимові; виробництво та споживання напоїв або морозива має періодичний характер; перевезення пасажирів автомобільним чи залізничним транспортом; споживання електроенергії у різні години доби, дні тижня, місяці року і т. ін.. Таким чином, компонентами динамічного ряду є тенденції (тренди), випадкові та, можливо, сезонні коливання.

Маючи справу із показниками ряду динаміки дослідник завжди намагається виявити головну закономірність розвитку явища в окремі проміжки часу. Це зводиться до виявлення головної тенденції, звільненої від дії різних випадкових факторів. З цією метою ряди динаміки піддають певній статистичній обробці, яка може бути елементарно простою, або більш складною, із застосуванням математичних методів. Завдання щодо їх використання зводиться до елімінування дії випадкових, другорядних причин, а також встановлення характеру дії основних причин, що визначають динаміку досліджуваного явища.

У разі, коли рівні динамічного ряду коливаються, то наочно виявити тенденцію розвитку явища не можна. Тоді для виявлення основної тенденції розвитку застосовують методи згладжування динамічного ряду або аналітичне вирівнювання ряду динаміки.

До найбільш простих методів згладжування динамічних рядів належать методи ступінчастої середньої та плинної середньої. Метод ступінчастої середньої (укрупнення інтервалів) полягає в тому, що рівні первинного динамічного ряду поєднуються в збільшені інтервали і розраховуються середні в кожному зі створених інтервалів.

Наприклад, утворюється новий динамічний ряд, в якому окремі інтервали – це об’єднання трьох інтервалів первинного динамічного ряду. В такому разі середня кожного укрупненого інтервалу розраховується так:

₁ = (у₁ + у₂ + у₃) : 3

₂ = (у₄ + у₅ + у₆) : 3

₃ = (у₇ + у₈ + у₉) : 3 і т. д.

Суть методу середньої плинноїполягає в тому, що середні обчислюються також за збільшеними інтервалами, але на відміну від попереднього методу здійснюється послідовне пересування меж збільшених інтервалів на один первинний інтервал до кінця динамічного ряду. У такому разі середні інтервалів розраховуються за формулами:

₁ = (у₁ + у₂ + у₃) : 3

₂ = (у₂ + у₃ + у₄) : 3

₃ = (у₃ + у₄ + у₅) : 3 і т. д.

Якщо значення рівнів похідного (згладженого) динамічного ряду не дають можливості встановити чітку тенденцію, проводять нове згладжування, при цьому беруть ще більші інтервали. Слід зауважити, що для об’єднання беруться інтервали первинного динамічного ряду. Згладжування повторюють доти, доки не виявиться чітка тенденція, або коли не залишиться три укрупнених інтервали, оскільки подальше згладжування вже не має сенсу. Через дві точки завжди можна провести лінію, але при цьому можна отримати результат, протилежний реальному стану.

2. Рівняння тренду, етапи визначення та обґрунтування найпридатнішого функціонального виду, суть параметрів

Якщо згладжування ряду динаміки не дає можливості виявити тенденцію розвитку або її характер, то відповідь на це питання можна напевне одержати за допомогою аналітичного вирівнюваннязаданого (вихідного) динамічного ряду методом найменших квадратів.

Метод аналітичного вирівнювання дає змогу не лише виявити тенденцію розвитку, а й кількісно виміряти її.

Під аналітичним вирівнюваннямряду динаміки у статистиці розуміють побудову функціїY = f(t), яка аналітично виражає залежність значень ознакиYвід часуt. Такі функції, а також їх графіки називаютьтрендовими кривими. За допомогою трендової кривої завжди можна виявити основну тенденцію розвитку явища, що вивчається, а також її характер.

Процес побудови трендової кривої складається з двох етапів:

• вибір виду функції f(t)

• обчислення параметрів функції f(t).

Вид функції f(t)можна встановити візуально за кореляційним полем з урахуванням економічної (фізичної тощо) суті явища, що вивчається.

Кореляційне поле (див. рис. 8.4) являє собою координатну площину tOyіз зображеними на ній точками з координатами (t_i, y_i).

Y

* * * * *

* * * * *

* * * *

* * * * *

* * * * *

* * * *

**

* *

0 t

Рис. 8.4. Кореляційне поле

На практиці при виборі виду тренду перевага звичайно віддається функціям, параметри яких мають чіткий економічний зміст:

• лінійна – у = a + bt –(a – середній початковий рівень ознаки,b– середній абсолютний приріст)

• квадратична, або параболічна – y = a + bt + ct ² – (a– середній початковий рівень ознаки, b – середня початкова швидкість зростання,с– середній приріст швидкості зростання)

• показникові – y = a·b ^t – (a – середній початковий рівень ознаки,b– середній темп зростання).

Після вибору виду залежності її параметри обчислюються за методом найменших квадратів. Цей метод забезпечує такий вибір параметрів тренду, щоб мінімізувати суму квадратів відхилень фактичних значень рівнів ряду від теоретичних рівнів, що розраховані за відповідних значень t.

Найпростішою формулою, що відтворює тенденцію розвитку, є лінійна функція:

Параметри тазгіднометоду найменших квадратів знаходяться рішенням системи нормальних рівнянь:

,

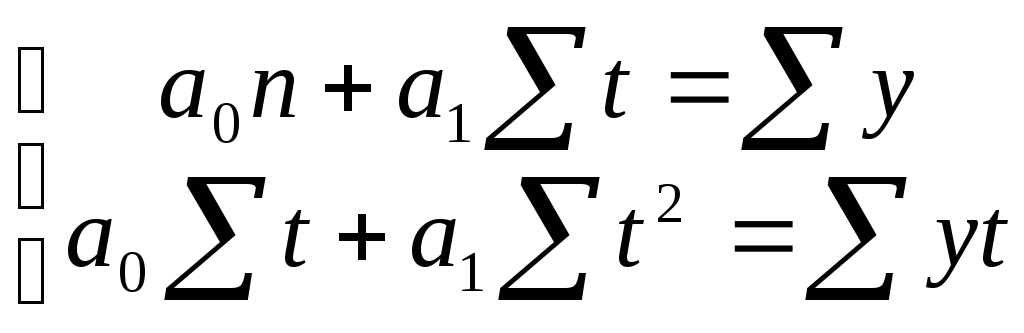де y– фактичні рівні ряду

t– порядковий номер періоду або моменту часу.

Розв’язавши цю систему, отримуємо значення параметрів лінійної моделі:

, ,

де – середній рівень динамічного ряду.

Розрахунок параметрів значно спрощується, якщо за початок відліку часу (t= 0) обрати центральний інтервал. Із використаннямспрощеного методу із введенням нумерації періодів часу від умовного нуля значення умовних періодівtзалежать від того, парну чи непарну кількість рівнів має динамічний ряд.

Якщо у трендовій моделі використовуються нелінійні функції, то вони приводяться до лінійного вигляду за допомогою певних математичних перетворень. Так, степенева функція призводиться до лінійного вигляду за допомогою логарифмування, гіпербола – заміною змінної.

2. Екстраполяція трендів як один із методів прогнозування рівнів соціально-економічних явищ

Зробити прогноз явища у означає обчислити значення ознаки Y на той майбутній період часу t, який нас цікавить. Очевидно, що будь-який прогноз може бути тільки наближеним і може вважатись реальним тільки за умови збереження у майбутньому тенденції розвитку явища та її характеру. Метод прогнозування на періоди за межами ряду динаміки (на майбутнє або за минулі періоди часу) називають екстраполяцією. Метод прогнозування на періоди пропущених періодів часу в середині ряду динаміки називають інтерполяцією.

Точковий прогнозздійснюється за допомогою екстраполяції трендової моделі, тобто прогнозоване значення явища обчислюється за встановленою формулою. При цьому слід мати на увазі той факт, що рівняння трендової кривої побудоване з використанням умовних періодів, а тому для визначення точкового прогнозу вводиться наступний період. Наприклад, якщо динамічний ряд містить шість періодів, то точкова оцінка розраховується для наступного, сьомого періоду (див. табл. 9.1)якщо динамічний ряд містить сім періодів, то точкова оцінка розраховується для наступного (умовного) четвертого періоду (див. табл. 9.2).

Інтервальний прогноз являє собою інтервал значень ознаки у, який із заданою ймовірністю покриває (або має покривати) справжнє значення:

,

де у_t– точковий прогноз

– довірче число, яке обирається з таблиць розподілу Стьюдента (якщо кількість рівнів динамічного ряду менше 30) або з таблиць нормального розподілу (якщо кількість рівнів динамічного ряду більша за 30)

– залишкове середнє квадратичне відхилення.

Залишкове середнє квадратичне відхилення розраховується за формулою:

,

де Y – фактичні рівні досліджуваного динамічного ряду

Y_t – теоретичні значення трендової моделі у відповідні періоди

n– кількість рівнів динамічного ряду

m –число параметрів трендової моделі (для лінійної моделіm= 2).

Такий інтервал називають довірчим інтервалом, а відповідну ймовірність – довірчою ймовірністю.

На відміну від точкового інтервальний прогноз може розроблятися лише на наступний період .