Змістовий модуль 3. Аналіз закономірностей динаміки

Тема 7. Аналіз інтенсивності динаміки

План вивчення теми

1. Поняття та складові елементи рядів динаміки (часових рядів). Передумови й об’єктивні умови для побудови рядів динаміки

2. Види рядів динаміки та їх особливості

3. Статистичні характеристики часових рядів: абсолютний приріст, темп зростання, темп приросту, абсолютне значення 1% приросту; їх взаємозв’язок

4. Середні характеристики часового ряду

5. Оцінка прискорення (уповільнення) розвитку. Порівняльний аналіз динамічних рядів; коефіцієнти випередження та еластичності, умови їх використання

Після вивчення теми студенти повинні:

• знати: в чому полягають передумови й об’єктивні умови для побудови рядів динаміки (часових рядів); зміст статистичних характеристик (абсолютних і відносних) рядів динаміки, їх взаємозв’язок;

• уміти: обґрунтовано використовувати на практиці основні статистичні характеристики (абсолютні та відносні) для аналізуінтенсивності динаміки, проводити порівняльний аналіз динамічних рядів.

Бібліографічний список: [7 – 10; 17 - 22 ]

7.1. Поняття та складові елементи рядів динаміки (часових рядів). Передумови й об’єктивні умови для побудови рядів динаміки

Суспільно-економічні явища безперервно змінюються. Протягом певного часу – місяць за місяцем, рік за роком змінюється кількість населення, обсяг та структура суспільного виробництва, рівень продуктивності праці тощо. Вивчення поступального розвитку й змін суспільних та економічних явищ – одне з основних завдань статистики.

Для кращого розуміння і аналізу зміни досліджуваних явищ у часі статистичні дані, що їх характеризують, необхідно систематизувати у хронологічному порядку і вже потім аналізувати. У статистиці це виконується за допомогою рядів динаміки або ще їх називають часовими рядами.

Отже, ряди динаміки – це ряди чисел, що характеризують закономірності зміни суспільних явищ і процесів у часі, тобто це сукупність значень статистичних показників , розташованих у хронологічному порядку.

Кожний ряд динаміки складається з двох елементів:

• числових значень статистичних показників (рівнів ряду) – y;

• періодів або моментів часу, яким відповідають рівні ряду – t.

Таким чином, під час вивчення динаміки важливі не лише числові значення рівнів, а й їх послідовність. Як правило, часові інтервали між рівнями однакові (доба, тиждень, місяць, квартал, півріччя, рік тощо). Якщо прийняти за одиницю довжину певного інтервалу, послідовність рівнів можна записати у вигляді:

у₁, у₂ , у₃ , у₄ , . . . , у_n ,

де у – рівень динамічного ряду

n – кількість рівнів (довжина динамічного ряду).

Ряди динаміки дозволяють охарактеризувати розвиток явища в часі, виявити тенденції зміни, а також за цими даними побудувати прогноз на наступний період лише в тому разі, коли вони правильно побудовані.

Основними правилами побудови й аналізу рядів динаміки є:

1. Періодизація розвитку.

2. Порівнянність рівнів ряду.

3. Відповідність розміру інтервалу інтенсивності розвитку явища.

4. Підпорядкованість динамічного ряду у часі.

2. Види рядів динаміки та їх особливості

Економічні та соціальні явища дуже різні і тому вони можуть бути представлені у хронологічному порядку у вигляді різних рядів динаміки. Класифікація рядів динаміки за чотирма напрямками представлена на рис. 7.1.

2. Статистичні характеристики часових рядів: абсолютний приріст, темп зростання, темп приросту, абсолютне значення 1% приросту; їх взаємозв’язок

Рядом динаміки є ряд послідовних рівнів, при співставленні яких між собою можна отримати характеристику швидкості та інтенсивності розвитку явища. У результаті такого порівнювання рівнів отримують систему абсолютних та відносних показників динаміки. Виконання розрахунків при цьому можливо у двох варіантах, які схематично представлені на рис. 7.2.:

• 1-й варіант - кожний рівень ряду динаміки порівнюється безпосередньо з попереднім, і таке порівняння називається порівнянням із змінною базою, а розраховані показники –ланцюговими характеристиками динаміки.

• 2-й варіант - кожний рівень ряду динаміки порівнюється з одним і тим же попереднім рівнем, який прийнято за базу порівняння. В якості базового рівня вибирають початковий рівень ряду динаміки, або рівень, з якого починається якийсь новий етап розвитку явища. Таке порівняння називається порівнянням з постійною базою, а розраховані показники – базисними характеристиками динаміки.

• Базисні показники характеризують кінцевий результат всіх змін у рівні ряду від періоду, до якого належить базисний рівень, до даного (і-го ) періоду.

• Ланцюгові показники характеризують інтенсивність зміни рівня від періоду до періоду (або від дати до дати) в межах проміжку часу, що вивчається.

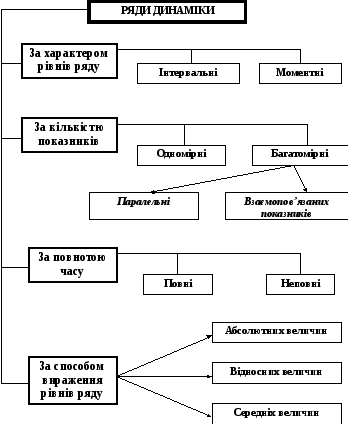
Рис. 7.1. Класифікація рядів динаміки

Абсолютний приріст (зменшення) _t - це показник ряду динаміки, який характеризує на скільки одиниць змінився поточний рівень показника порівняно з рівнем попереднього або базового періоду. Абсолютний приріст із змінною базою виражає абсолютну швидкість зміни рівнів ряду динаміки. Розраховується абсолютний приріст як різниця двох рівнів динамічного ряду:

ланцюговий _t = у_t - y_{t -1},

базисний _t = y_t - y₀.

Між ланцюговими та базисними показниками існує взаємозв’язок – сума ланцюгових абсолютних приростів дорівнює кінцевому базисному:

Коефіцієнт зростання - це показник ряду динаміки, який показує:

у скільки разів зріс поточний (порівнюваний) рівень показника, що аналізується, порівняно з рівнем попереднього (базового) періоду – якщо значення коефіцієнту зростання К_t > 1;

яку частку становить поточний (порівнюваний) рівень показника до рівня попереднього (базового) періоду періоду – якщо значення коефіцієнту зростання К_t < 1;

що ніяких змін не відбулося - якщо значення коефіцієнту зростання К_t =1.

Коефіцієнт зростання К_t розраховується як відношення рівнів ряду і виражається коефіцієнтом:

ланцюговий К _t = y_t / y _t--1,

базисний К _t = y_t / y_{0 .}

Зв’язок між ланцюговими і базисними коефіцієнтами зростання полягає в тому, що добуток ланцюгових коефіцієнтів зростання дорівнює кінцевому базисному:

.

Темп зростання – це коефіцієнт зростання, але представлений у відсотках, тобто

Т_р = К_t · 100,

або для ланцюгових Т_р = (y_t / y _t—1)·100,

для базисних Т_р = (y_t / y₀)·100.

Темп приросту - це показник ряду динаміки, який показує на скільки відсотків змінився поточний (порівнюваний) рівень аналізованого показника порівняно з рівнем попереднього або базового періоду. Його можна визначити як відношення абсолютного приросту до бази порівняння або безпосередньо на основі темпу зростання.

Для ланцюгових характеристик:

Т_пр = 100 · _t / y _t—1 = 100 (y_t – y_t—1 ) / y _t—1 = 100 (К_t – 1) = Т_р - 100.

Аналогічно взаємопов’язані і базисні темпи приросту.

Абсолютне значення одного відсотка приросту — це відношення абсолютного приросту до відповідного темпу приросту або одна сота попереднього рівня. Абсолютне значення 1 % приросту показує, чого вартий 1% і розраховується як співвідношення абсолютного приросту й темпу приросту. Алгебраїчно це співвідношення дорівнює 0,01 рівня, взятого за базу порівняння:

А% = _t / Т_пр =( y_t - y _t—1)/ 100 (y_t - y_t—1)/ y_t--1 = y_t--1 / 100 = 0,01 y_t—1.

Для базисних темпів приросту значення А% однакові, тому їх не розраховують.

2. Середні характеристики часового ряду

Середній рівень динамічного ряду - середня, обчислена на основі рівнів динамічного ряду. Особливості розрахунку залежать від виду ряду динаміки, він визначається як середня арифметична проста (якщо рівні ряду представлені інтервальними абсолютними величинами), середня арифметична зважена (якщо рівні ряду представлені моментними величинами із нерівними періодами часу між моментами) або середня хронологічна (якщо рівні ряду представлені моментними величинами із рівними періодами часу між моментами).

Середній або середньорічний абсолютний приріст - це показник ряду динаміки, який показує на скільки одиниць у середньому за одиницю часу (щорічно) за певний період змінювався рівень показника, що аналізується. Середній абсолютний приріст розраховується як середня арифметична проста з ланцюгових абсолютних приростів:

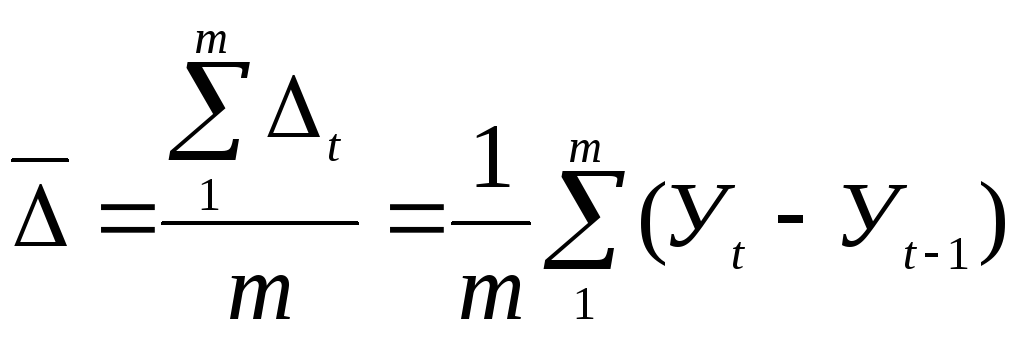або ,

де m = n - 1 - число ланцюгових абсолютних приростів,

n – число періодів (моментів) у ряду динаміки.

Середній або середньорічний темп зростання - це показник ряду динаміки, який показує скільки відсотків у середньому за одиницю часу (щорічно) за певний період становить зміна рівня показника, що аналізується. Середній або середньорічний темп приросту - це показник ряду динаміки, який показує на скільки відсотків у середньому за одиницю часу (щорічно) за певний період змінювався рівень показника, що аналізується. Ці показники краще розраховувати після визначення середнього або середньорічного коефіцієнта зростання (росту).

Середній коефіцієнт зростання розраховують за формулою середньої геометричної:

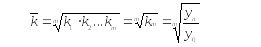
де m - число ланцюгових коефіцієнтів зростання; m = n – 1.

Якщо відомий середній коефіцієнт зростання, то середній темп зростання та середній темп приросту визначають наступним чином:

·100%.

2. Оцінка прискорення (уповільнення) розвитку. Порівняльний аналіз динамічних рядів; коефіцієнти випередження та еластичності, умови їх використання

Якщо абсолютна та відносна швидкість динаміки у межах періоду, що вивчається, неоднакова, порівнянням однойменних характеристик за різні інтервали часу вимірюється прискорення (уповільнення) динаміки.

Різниця абсолютних ланцюгових приростів ' = _t -  _t--1 характеризує абсолютне прискорення (+) чи уповільнення (-) динаміки.

Відносне прискорення — це відношення абсолютного прискорення до абсолютного приросту, прийнятого за базу ( Δ' / Δ_іб ) або це темп приросту абсолютного приросту. Розраховується тільки у випадку, якщо абсолютний приріст, прийнятий за базу порівняння, додатне число. Якщо інтервали часу неоднакові, використовують середні абсолютні прирости відповідних інтервалів.

При порівнюванні розвитку двох явищ використовують показники, що являють співвідношення базисних темпів зростання або темпів приросту за однакові відрізки часу за двома рядами динаміки. Ці показники називають коефіцієнтами випередження:

К_в = Т_р^А / Т_р^Б, або К_в = Т_пр^А / Т_пр^Б.

За допомогою цих показників порівнюють ряди динаміки, що мають однаковий зміст, але належать до різних територій або об’єктів, а також ряди динаміки різного змісту, що характеризують один і той же об’єкт.

Якщо ряди динаміки взаємопов’язані, тобто рівні їх являють собою фактор х та результат у, із співвідношення темпів приросту цих ознак визначають, на скільки відсотків змінюється результативна ознака у зі зміною факторної ознаки х на 1 %. За економічним змістом співвідношення темпів приросту є коефіцієнтом еластичності :

К_ел = Т_{пр у} / Т_{пр х}.

Під час аналізу статистичних характеристик неповних рядів динаміки слід пам’ятати про зв’язок, що існує між базисними та ланцюговими абсолютними приростами та коефіцієнтами росту. Цей взаємозв’язок допомагає визначити характеристики за відсутні у ряді динаміки проміжки часу.