5.4. Середні величини у статистиці, їх види, умови наукового застосування та особливості обчислення

Однією з узагальнюючих характеристик в аналізі суспільних явищ є середня величина. Статистичні середні відображують об'єктивну наявність певних умов, які проявляються в кожній одиниці досліджуваної сукупності. Середня узагальнює весь діапазон даних і є результатом абстрагування відмінностей, що притаманні одиницям сукупності. У ній нівелюються випадкові відхилення, властиві індивідуальним значенням ознаки, яка вивчається, а також відображаються загальні умови, що формують досліджувану сукупність.

Порівняти ж між собою окремі сукупності за якоюсь конкретною ознакою можна за середнім її значенням, визначеним для кожної сукупності. Це можливо тому, що в середній величині відображається те типове, що характерне для всієї сукупності.

Розраховуючи конкретну середню, завжди доцільно опиратись на її логічну формулу (математичне вираження середньої), яка є відношенням обсягу ознаки до обсягу сукупності. Критерій правильного вибору форми середньої величини - це запис логічної формули розрахунку.

Для кожної середньої є лише одне правильне співвідношення, для реалізації якого залежно від даних, що існують, можна використовувати різні форми середніх: середню арифметичну, середню гармонічну, середню квадратичну, середню геометричну за не згрупованими (просту) і за згрупованими даними (зважену).

Однак в усіх випадках, коли характер величини, за якою розраховується середня, передбачає наявність ваги, неможливо замість зважених формул середніх використовувати прості, тобто незважені, формули. Використання кожного виду середніх залежить від двох обставин, по-перше, від характеру індивідуальних значень ознаки (прямі, обернені, квадратичні, відносні). По-друге, від характеру алгебраїчного зв’язку між індивідуальними значеннями ознаки та її загальним обсягом (сума, добуток, степень, квадратичний корінь).

Середня арифметична – використовується для усереднення прямих значень ознак шляхом їх підсумовування. Якщо дані не згруповані:

,

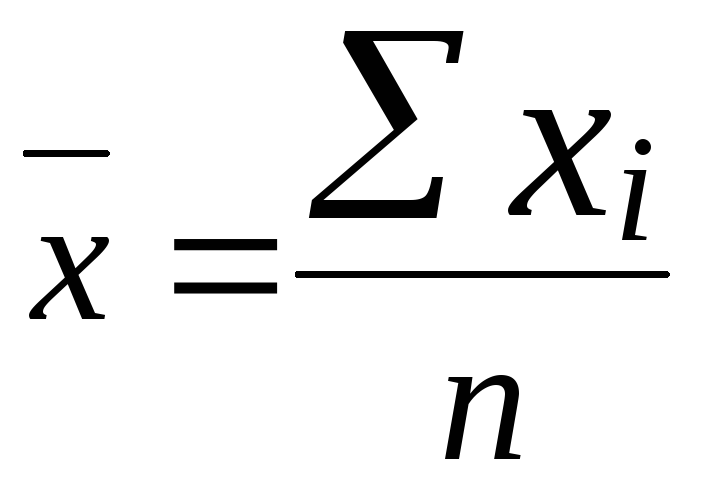де - варіанти, тобто значення ознаки, що осереднюється дляi- ої одиниці сукупності;

n – число одиниць у сукупності.

Якщо дані згруповані, то використовують середню арифметичну зважену, яку розраховують за формулою:

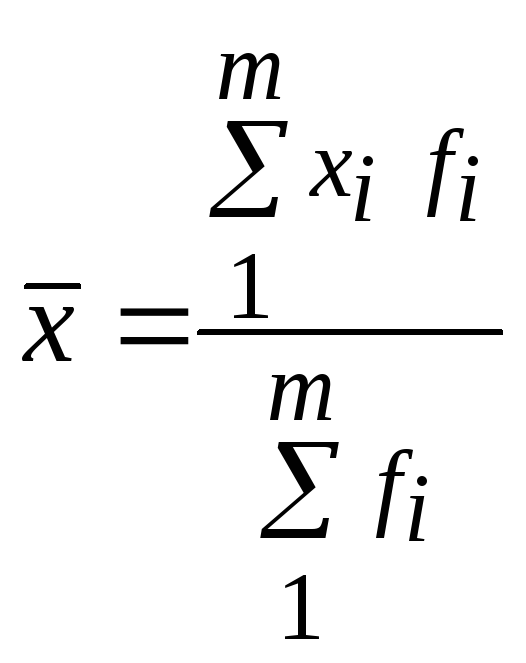, або ,

де - частота; – частка-ї групи.

При цьому

а .

Середня гармонічна використовується для осереднення обернених індивідуальних значень ознак шляхом їх підсумовування. Для не згрупованих даних це середня гармонічна проста

.

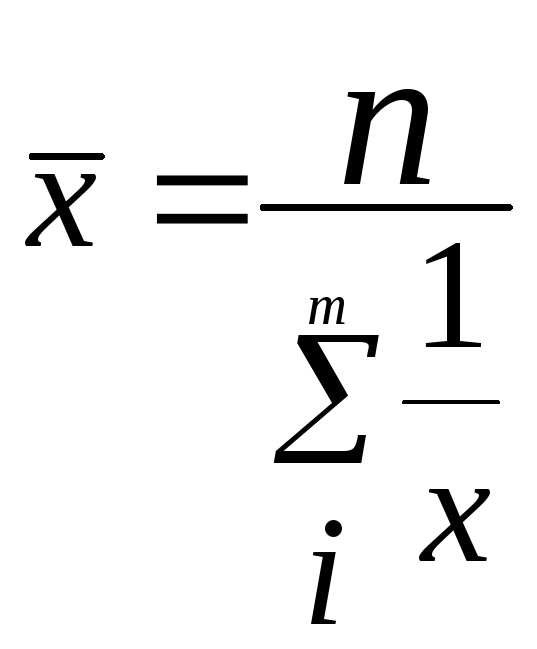Якщо дані згруповані, то використовують середню гармонічну зважену

,

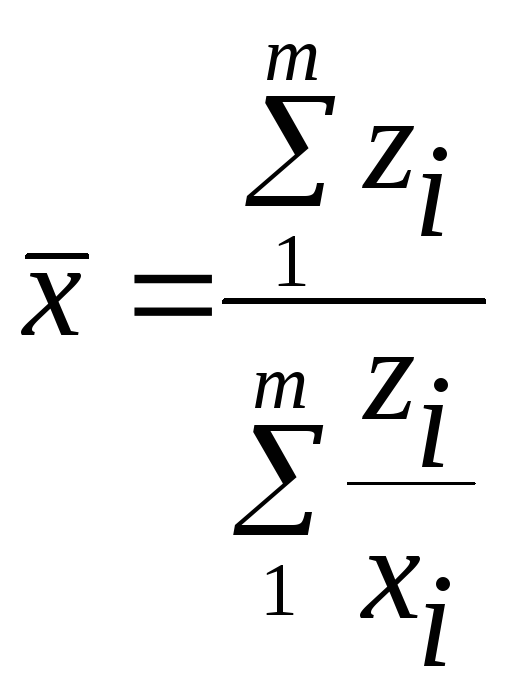де - обсяг значень ознаки, тобто..

Очевидно, що середню гармонічну зважену доцільно використовувати, коли відсутня інформація про значення знаменника логічної формули, тобто відсутні ваги у явному виді.

Середня геометрична визначається як добуток відносних величин динаміки , які є кратним співвідношенням-го значення показника до попереднього (-1). Формуласередньої геометричної простої

,

де - символ добутку;

- кількість величин, середня яких обчислюється.

Якщо часові інтервали неоднакові, використовують середню геометричну зважену

,

де - часовий інтервал.

У інтервальних рядах, припускаючи рівномірний розподіл у межах -го інтервалу, як варіантвикористовують середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою ж, як і сусіднього закритого інтервалу.

Середня арифметична має певні математичні властивості.