
- •Курс лекций
- •2. Решение волнового уравнения методом Фурье
- •Кратные интегралы Лекция № 51. Тема 1: Определение кратного интеграла
- •1.1. Задачи, приводящие к понятию кратного интеграла
- •1.2. Определение кратного интеграла и его основные свойства
- •Тема 2: Двойной интеграл
- •2.1. Определение двойного интеграла
- •2.2. Вычисление двойного интеграла.
- •Лекция № 52
- •2.3. Замена переменных в двойном интеграле.
- •2.4. Двойной интеграл в полярной системе координат
- •2.5. Приложения двойного интеграла
- •. Лекция № 53
- •Лекция № 54. Тема 3 : Тройной интеграл
- •3.1. Определение и вычисление тройного интеграла
- •3.2. Замена переменных в тройном интеграле
- •3.3. Приложения тройного интеграла
- •Лекция № 55. Тема 4 : Криволинейные интегралы
- •4.1. Криволинейные интегралы первого рода или по длине дуги
- •4.2. Криволинейные интегралы второго рода или по координатам
- •Лекция № 56.
- •4.3. Формула Грина
- •4.4. Условие независимости криволинейного интеграла второго рода от пути интегрирования
- •Тема 5 : Поверхностные интегралы
- •5.1. Поверхностные интегралы первого рода
- •5.2. Поверхностные интегралы второго рода
- •5.3. Приложения поверхностных интегралов
- •Лекция № 57. Тема 6 : Элементы теории поля
- •6.1. Понятие поля
- •6.2. Формула Гаусса Остроградского
- •6.3. Формула Стокса
- •Теория вероятностей Лекция № 58. Тема 1 : Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •Лекция № 59
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •Лекция № 60. Тема 2 : Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •Лекция № 61. Тема 3 : Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •Лекция № 62. Тема 4 : Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Непрерывная св. Функция распределения
- •Лекция № 63. Тема 5 : Числовые характеристики св
- •5.1. Математическое ожидание св
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Понятие о моментах св
- •Лекция № 64. Тема 6 : Основные законы распределения случайных величин
- •6.1. Дискретные законы распределения
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Непрерывные законы распределения
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •Лекция № 65
- •6.2.3. Нормальное распределение
- •Тема 7 : Закон больших чисел
- •Лекция № 66. Тема 8 : Многомерные случайные величины
- •8.1. Многомерные св и их функции распределения
- •8.2. Числовые характеристики двумерной случайной величины
- •Элементы математической статистики Лекция № 67. Введение
- •1. Предмет математической статистики
- •Тема 1: Статистические законы распределения выборки
- •1.1. Полигон и гистограмма
- •1.2. Эмпирическая функция распределения
- •Тема 2 : Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •Лекция № 68
- •Тема 3 : Проверка статистических гипотез. Критерий согласия Пирсона
- •Тема 4 : Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
- •Теория функций комплексной переменной Лекция № 69. Определение функции комплексной переменной
- •1.1. Комплексные числа и действия над ними
- •1.2. Тригонометрическая и показательная формы записи
- •1.3. Определение функции комплексной переменной
- •Лекция № 70
- •1.3. Предел и непрерывность функции комплексной переменной
- •Тема 2 : Ряды с комплексными членами
- •2.1. Числовые ряды
- •2.2. Степенные ряды
- •2.3. Основные элементарные функции комплексной переменной
- •Лекция № 71. Тема 3 : Производная функции комплексной переменной
- •3.1. Определение производной
- •3.2. Гармонические функции
- •Тема 4 : Интеграл от функции комплексной переменной
- •4.1. Определение интеграла
- •4.2. Основная теорема Коши
- •Лекция № 72
- •4.3. Интегральная формула Коши
- •4.4. Производные высших порядков от аналитической функции
- •4.5. Ряд Тейлора
- •. . . . .
- •4.6. Ряд Лорана
- •Лекция № 73
- •Тема 5 : Вычеты
- •5.1. Изолированные особые точки аналитической функции
- •5.2. Определение вычета
- •5.3. Основная теорема о вычетах
- •5.4. Приложение вычетов к вычислению интегралов
- •Операционное исчисление Лекция № 74. Тема 1 : Оригинал и изображение
- •1.1. Определение оригинала и изображения
- •1.2. Изображения некоторых функций
- •Тема 2 : Основные теоремы операционного исчисления
- •2.1. Теоремы подобия, запаздывания и смещения
- •Лекция № 75.
- •3.2. Приложение операционного исчисления к задачам техники
- •С о д е р ж а н и е
3.2. Приложение операционного исчисления к задачам техники
Наиболее широко операционное исчисление применяется в задачах электротехники и автоматического управления, в частности при изучении переходных процессов в линейных физических системах. Остановимся на его применении в задачах механики и автоматики.
Пример 4.
Рассмотрим задачу о движении материальной
точки массой
![]() под действием силы веса, силы упругости
(действие пружины) и силы сопротивления,
которая пропорциональна скорости
движения
под действием силы веса, силы упругости
(действие пружины) и силы сопротивления,
которая пропорциональна скорости
движения
![]() .
Требуется найти скорость движения
.
Требуется найти скорость движения
![]() материальной точки.
материальной точки.
Представим силу упругости в виде
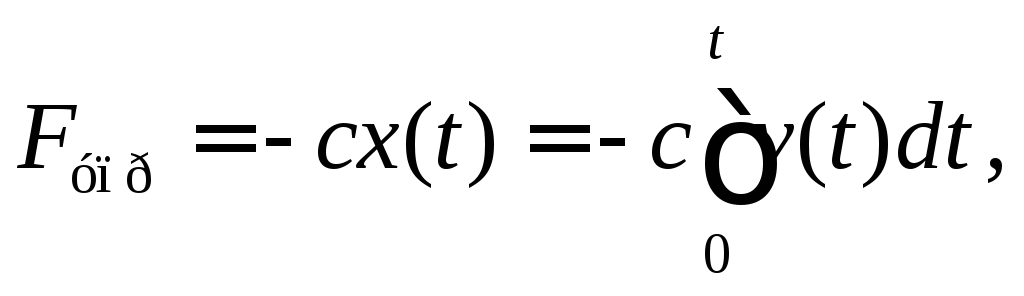
где с
коэффициент, характеризующий упругие
свойства пружины,
![]()
перемещение точки. Тогда, согласно
второму закону Ньютона, получим уравнение
перемещение точки. Тогда, согласно
второму закону Ньютона, получим уравнение
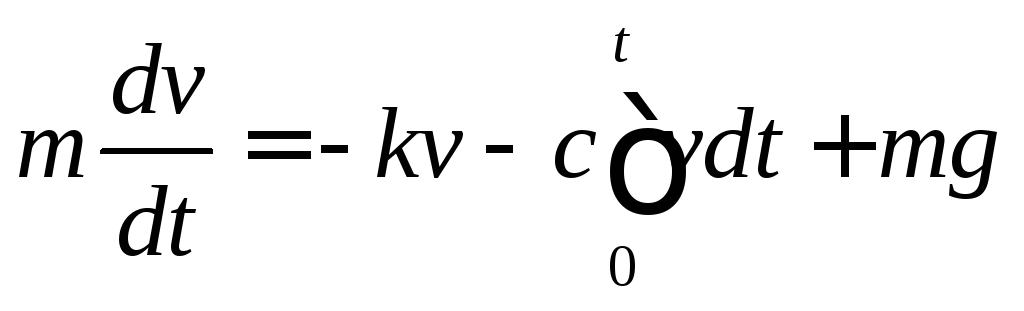 или
или
 (3)
(3)
Уравнение (3)
является интегрально-дифференциальным
уравнением для определения скорости
движения
![]() .
Применим к нему преобразование Лапласа
с учётом, что начальная скорость
была
.
Применим к нему преобразование Лапласа
с учётом, что начальная скорость
была
![]() :
:
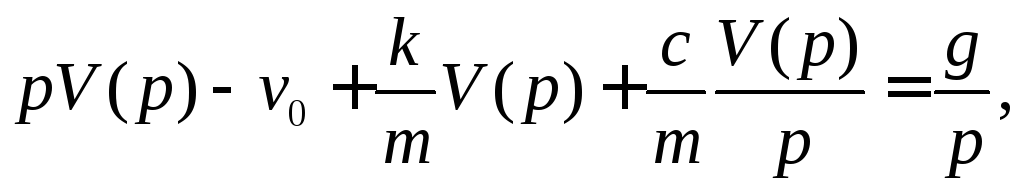 (4)
(4)
где
![]() .
.
Из уравнения (4) определяем изображение
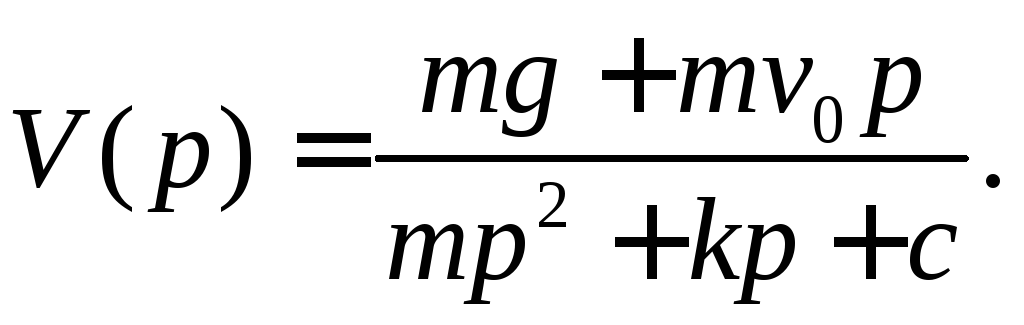 (5)
(5)
Определить оригинал
(искомую скорость) по изображению (5) не
представляет затруднений (см., например,
теорему разложения). Всё зависит от
значений коэффициентов:
![]() .
В реальных процессах изменение скорости
будет представлять собой затухающие
гармонические колебания, т.е. уравнение
вида
.
В реальных процессах изменение скорости
будет представлять собой затухающие
гармонические колебания, т.е. уравнение
вида
![]()
Пример 5.
Найти решение дифференциального
уравнения
![]() где функция
где функция![]()
имеет обычный для автоматических
п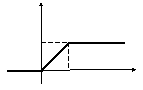 роцессов
кусочно-непрерывный вид
роцессов
кусочно-непрерывный вид![]()
 1
1
а начальные данные
![]() 0 1 t
0 1 t
Левая часть дифференциального уравнения имеет изображение
![]()
а изображение правой части найдем, используя теорему запаздывания.
С помощью единичной
функции данную функцию
![]() можно представить в следующем виде
можно представить в следующем виде
![]()
и тогда по таблице изображений имеем
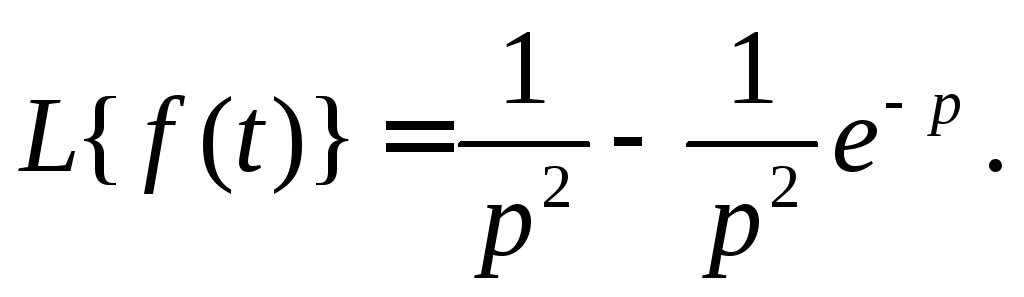
Таким образом, дифференциальное уравнение примет вид
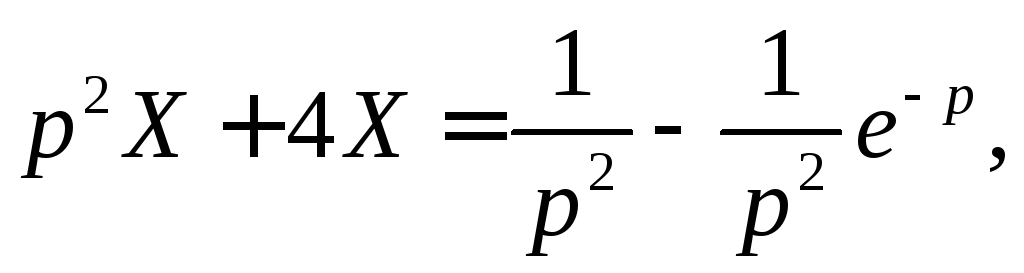
откуда
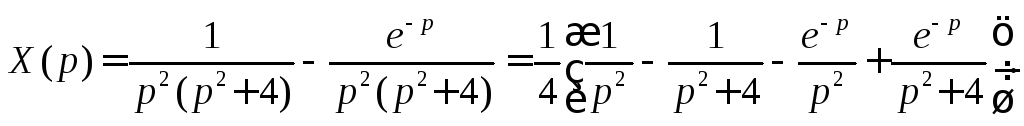
Переходя от изображения к оригиналу, окончательно получим
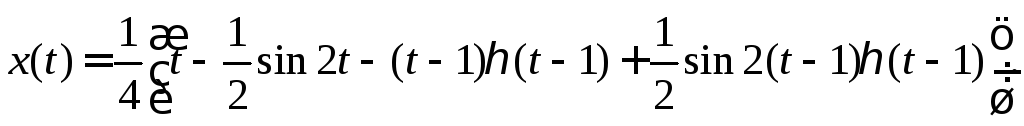
С о д е р ж а н и е
Лекция № 50. Тема : Уравнения математической физики . . . . . . 1
Основные типы уравнений математической физики (1).
Решение волнового уравнения методом Фурье (1).
Лекция № 51. Тема : Определение кратного интеграла . . . . . . . 5
Задачи, приводящие к понятию кратного интеграла (5). Определение
кратного интеграла (5). Основные свойства кратного интеграла (6).
Тема : Двойной интеграл . . . . . . . . . . . . . . 7
Определение двойного интеграла (7). Вычисление двойного интеграла (8).
Лекция № 52. Тема : Двойной интеграл (продолжение) . . . . . . . 10
Замена переменных в двойном интеграле (10). Двойной интеграл в
полярной системе координат (11). Приложения двойного интеграла: площадь плоской фигуры (12).
Лекция № 53. Тема : Двойной интеграл (окончание) . . . . . . . . . 14
Приложения двойного интеграла: объем тела (14), площадь поверх-ности (14), масса плоской фигуры (15), центр масс плоского тела (16), моменты инерции (17).
Лекция № 54. Тема : Тройной интеграл . . . . . . . . . . . . . . 18
Определение и вычисление тройного интеграла (18). Замена переменных в тройном интеграле (18). Приложения тройного инте-грала: объем тела (20), центр масс тела (20), моменты инерции (22).
Лекция № 55. Тема : Криволинейные интегралы . . . . . . . . . . 23
Криволинейные интегралы первого рода или по длине дуги: определение интеграла (23), вычисление интеграла (23), вычисление длины дуги (24), вычисление центра масс линии (24). Криволинейные интегралы второго рода или по координатам: определение интеграла (25), вычисление интеграла (26), вычисление работы силы (26).
Лекция № 56. Тема : Криволинейные интегралы (окончание) . . . . . 27
Формула Грина (27). Условие независимости криволинейного интеграла второго рода от пути интегрирования (28).
Тема : Поверхностные интегралы . . . . . . . . . . 29
Поверхностные интегралы первого рода (29). Поверхностные инте-гралы второго рода (30). Приложения поверхностных интегралов (32).
Лекция № 57. Тема : Элементы теории поля . . . . . . . . . . . . 33
Понятие поля (33). Формула Гаусса – Остроградского (34). Формула Стокса (35).
Лекция № 58. Тема : Общие понятия теории вероятностей . . . . . 38
Предмет теории вероятностей (38). Пространство элементарных событий (38). Операции над событиями (39). Статистический подход к понятию вероятности (41).
Лекция № 59. Тема : Общие понятия теории вероятностей (окончание) . 42
Элементы комбинаторики (42). Классическое определение веро-ятности (44). Аксиоматическое определение вероятности (45).
Лекция № 60. Тема : Основные теоремы теории вероятностей . . . . 46
Теорема умножения вероятностей (46). Теорема сложения вероятнос-тей (46). Формула полной вероятности (47). Формула Бейеса (48).
Лекция № 61. Тема : Повторение испытаний . . . . . . . . . . . . 49
Независимые испытания. Формула Бернулли. (49). Локальная теорема Муавра – Лапласа (50). Интегральная теорема Лапласа (51). Теорема Пуассона (52). Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях (53).
Лекция № 62. Тема : Случайные величины и функции распределения . 54
Случайные величины (54). Функция распределения вероятностей для дискретной СВ (55). Непрерывная СВ. Функция распределения и плотность распределения вероятностей (56).
Лекция № 63. Тема : Числовые характеристики случайных величин . . 57
Математическое ожидание (57). Дисперсия (59). Понятие о моментах (60).
Лекция № 64. Тема : Основные законы распределения СВ . . . . . . 61
Дискретные законы распределения: биномиальное распределение (61), распределение Пуассона (62), геометрическое распределение (62). Непрерывные законы распределения: равномерное распределение (63), показательное распределение (64).
Лекция № 65. Тема : Основные законы распределения СВ (окончание) . 66
Непрерывные законы распределения: нормальное распределение (66).
Тема : Закон больших чисел . . . . . . . . . . . . . 68
Неравенство Чебышева (68). Теорема Чебышева (69).
Лекция № 66. Тема : Многомерные случайные величины . . . . . . 70
Многомерные случайные величины и их функции распределения (70). Числовые характеристики двумерной случайной величины (72).
Лекция № 67. Тема : Элементы математической статистики. Введение . 74
Тема : Статистические законы распределения выборки . 74
Полигон и гистограмма (74). Эмпирическая функция распределения (76).
Тема : Статистические оценки параметров распределения 77
Точечные оценки (77). Интервальные оценки (78).
Лекция № 68. Тема : Проверка статистических гипотез.
Критерий согласия Пирсона . . . . . . . . . . 80
Тема : Элементы теории корреляции . . . . . . . . . 82
Статистические зависимости (82). Линейная регрессия (83). Корреля-ционная таблица (84). Выборочный коэффициент корреляции (85).
Лекция № 69. Тема : Функции комплексной переменной . . . . . . . 86
Комплексные числа и действия над ними (86). Тригонометрическая и показательная формы записи комплексного числа (86). Определение функции комплексной переменной (88).
Лекция № 70. Тема : Функции комплексной переменной (окончание) . 90
Предел и непрерывность функции комплексной переменной (90).
Тема : Ряды с комплексными членами . . . . . . . . 91
Числовые ряды (91). Степенные ряды (92). Основные элементарные функции комплексной переменной (92).
Лекция № 71. Тема : Производная функции комплексной переменной . 94
Определение производной (94). Гармонические функции (96).
Тема : Интеграл от функции комплексной переменной . 97
Определение интеграла (97). Основная теорема Коши (98).
Лекция № 72. Тема : Интеграл от функции комплексной переменной . 99
Интегральная формула Коши (99). Ряд Тейлора (100). Ряд Лорана (101).
Лекция № 73. Тема : Вычеты . . . . . . . . . . . . . . . . . . . 103
Изолированные особые точки аналитической функции (103). Определение вычета (104). Основные теоремы о вычетах (106). Приложения вычетов к вычислению интегралов (106).
Лекция № 74. Тема : Операционное исчисление . . . . . . . . . . . 108
Определение оригинала и изображения (108). Изображение некоторых функций (109).
Тема : Основные теоремы операционного исчисления . 110
Теоремы подобия, запаздывания и смещения (110).
Лекция № 75. Тема : Основные теоремы операционного исчисления . 112
Теорема о свертке (112). Теорема о дифференцировании оригинала (112). Теорема о дифференцировании изображения (113). Теорема об интегрировании оригинала (113). Теорема об интегрировании изобра-жения (114). Теорема разложения (114).
Лекция № 76. Тема : Приложения операционного исчисления . . . . . 116
Решение линейных дифференциальных уравнений и систем с посто-янными коэффициентами (116). Приложения операционного исчисле-ния к задачам техники (118).
