Лекция № 68

Тема 3 : Проверка статистических гипотез. Критерий согласия Пирсона

Часто в задачах практики на основании тех или иных данных делается предположение о виде закона распределения интересующей нас случайной величины. Однако, для окончательного решения вопроса о виде закона распределения нужно проверить насколько сделанные предположения согласуются с опытными данными. Таким образом, необходимы критерии, которые позволили бы исследовать как согласуются наблюдаемые значения: случайной величины X с гипотезой относительно её функции распределения. Такие критерии называются критериями согласия. В основе их построения лежит исследование меры отклонения теоретической функции распределения от эмпирической

Наиболее распространённой такой мерой является мера, введённая Пирсоном

. (1)

Множество значений случайной величины Х разбито на т полу-интервалов без общих точек

. . . . .

[ [ [ [ [

Здесь  частота появления признака, принадлежащего интервалу . Очевидно, что объём выборки .

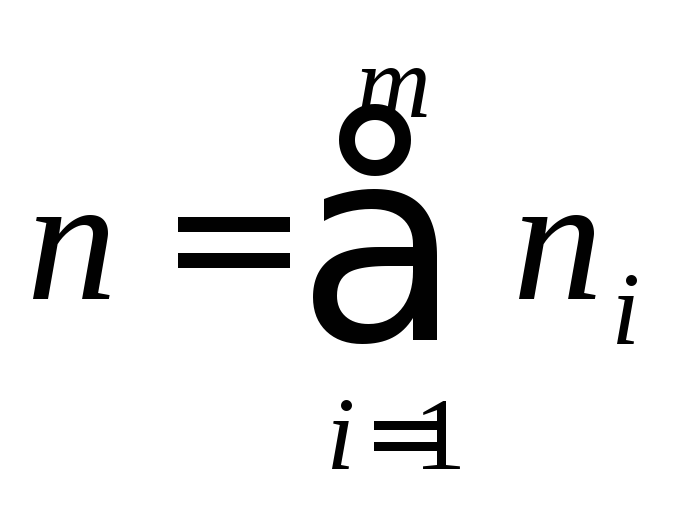Теоретические частоты , соответствующие эмпирическим, вычис-лены по предполагаемому закону распределения (гипотеза), для них также выполняется равенство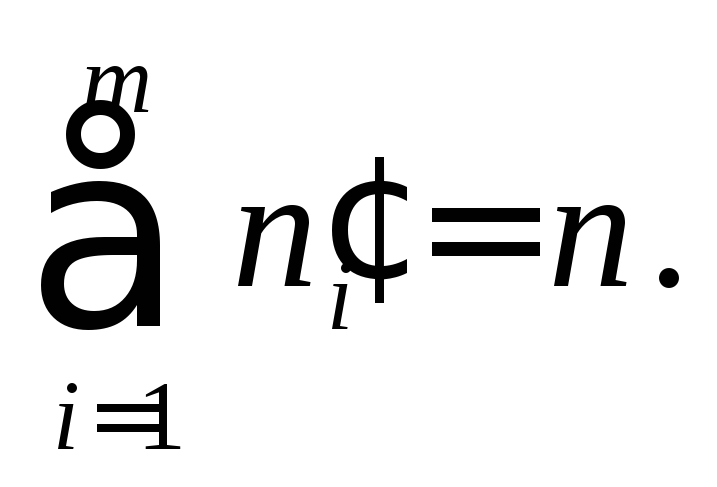

Величина является случайной величиной, при этом ее распреде-ление не зависит от функции распределения случайной величиныX и стре-мится при к так называемому-распределению сстепенями свободы, гдеr  число параметров теоретического закона.

Из этого следует критерий для проверки гипотезы о распределении изучаемой случайной величины (критерий Пирсона). Рассмотрим его при-менение для проверки гипотезы о нормальном распределении.

Пусть эмпирическое распределение задано в виде вариационного ряда равноотстоящих вариант с шагом h

			…
			…

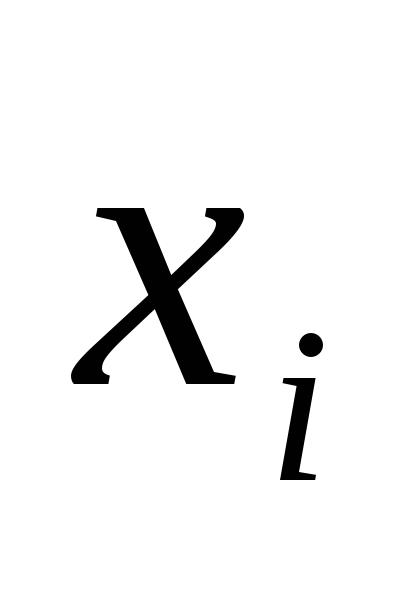
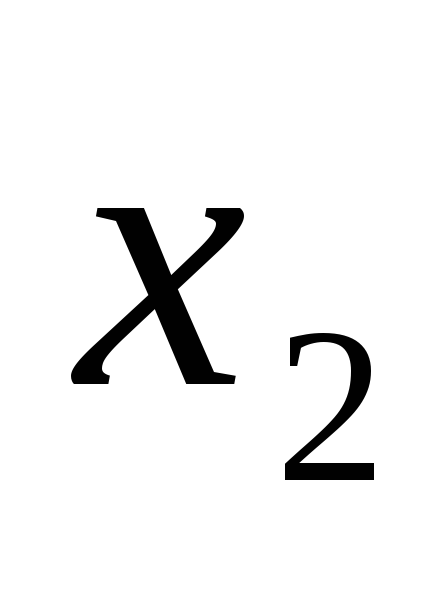
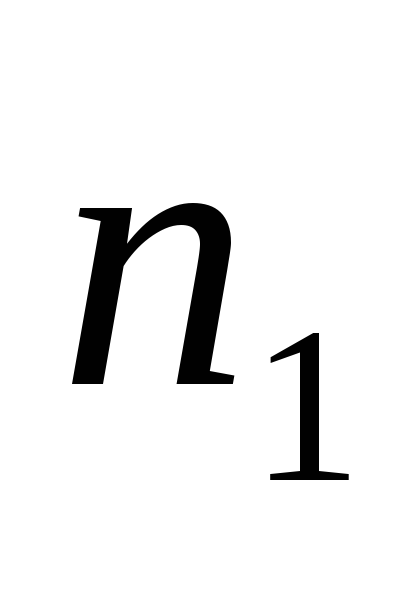
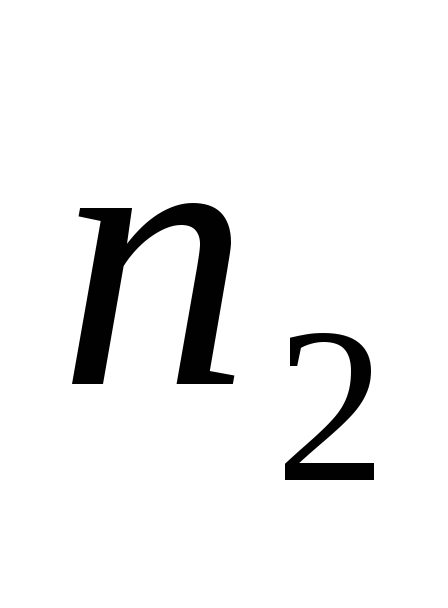
Необходимо:

1. Вычислить выборочное среднее

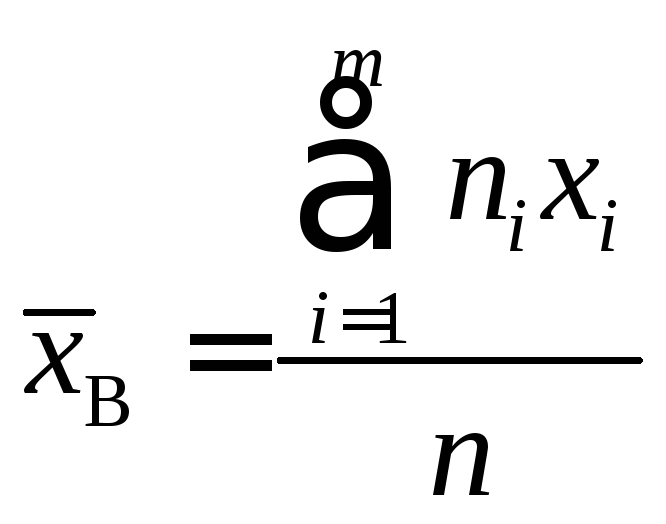
и исправленное выборочное среднее квадратическое отклонение

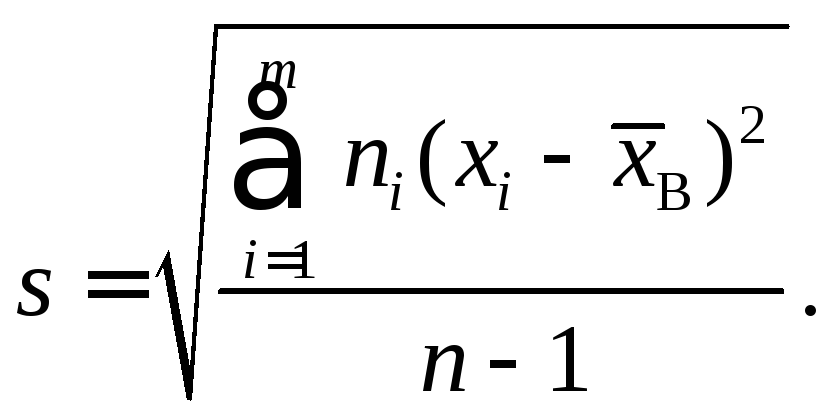
2. Определить теоретические частоты, считая закон распределения нормальным, т.е.

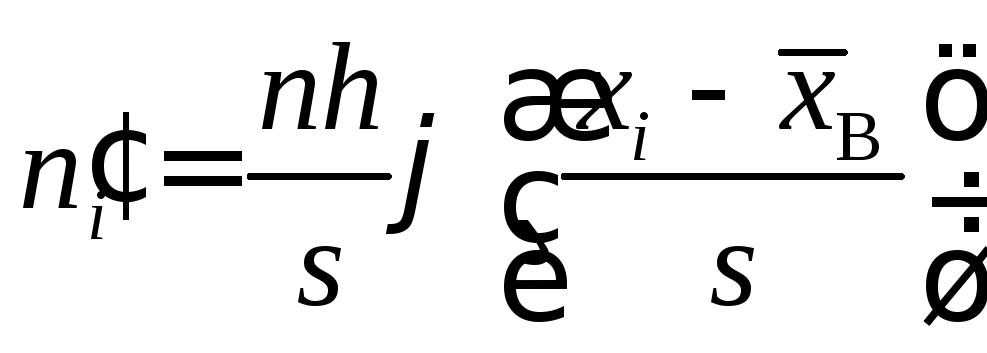, (2)

где

.

3. По формуле (1) вычислить величину . Пусть она оказалась равной.

4. Определить число степеней свободы для нормального распределения

5. По таблице критических точек распределения , по заданному уровню значимостии числу степеней свободыk находим критическую точку . Если , то гипотеза о нормальном распределении принимается, т.е. эмпирические и теоретические частоты различаются незначительно. В противном случае гипотеза отвергается.

Уровень значимости означает, что вероятность, т.е. осуществление такого события практически невозможно.

Замечание 1. Рассмотренный критерий на практике даёт хорошие результаты, если .

Пример 1. Проверить, согласуются ли данные таблицы с предполо-жением, что рост мужчины является нормально распределённой случайной величиной, приняв уровень значимости

156	11	11	0
160	26	27	0,0370
164	65	65	0
168	120	120	0
172	181	176	0,1420
176	201	199	0,0201
180	170	175	0,1429
184	120	122	0,0328
188	64	66	0,0606
192	28	28	0
196	14	11	0,8182
Итого	1000	1000	1,2536

Из таблицы следует, что ,и теоретические частотыопределяем по формуле (2).

Таким образом, . По уровню значимости и числу степеней свободыпо таблице критических точек распределениянаходим=20,1. Так как , то гипотеза принимается.