1.7. Аксиоматическое определение вероятности

Аксиоматический подход основывается на основных свойствах вероятности, подмеченных на примерах классического определения и частоты.

Пусть Е - пространство элементарных событий, а  класс событий (набор подмножеств множества E). Будем считать, что в результате любых введенных выше операций над событиями, вновь получаются события этого же класса.

Пример 11. Опыт состоит из подбрасывания игральной кости один раз. Здесь . Выпишем все события, которые образуют. Тогда.

Замечание. Число подмножеств множества из N элементов с учетом Е и равно. Например, в рассмотренном выше примере число таких подмножеств равно.

Определение 2. Числовая функция Р, определяемая на классе событий , называется вероятностью, если выполнены следующие аксиомы:

1. ;

2. ;

3. Если несовместные события, то

.

Из этого определения следуют свойства:

1. .

Действительно, так как или, с учетом аксиом2 и , получаем .

2. .

Действительно, так как , то с учетом свойства1 и аксиомы 2, получаем .

3. Если образуют полную группу событий, т.е., то.

Это следует из аксиом 23.

4. .

Это следует из свойства 3 и аксиомы 1.

Лекция № 60. Тема 2 : Основные теоремы теории вероятностей

2.1. Теорема умножения вероятностей

Определение 1. Условной вероятностью события B при условии, что событие A произошло, называется вероятность, определяемая формулой

. (1)

Это можно легко показать для случая классического определения веро-ятности. Будем считать, что формула справедлива в общем случае и про-иллюстрируем её на примере.

Пример 1. В урне 3 белых и 3 синих шара. Из урны вынут один шар, затем второй. Рассмотрим два события: A – первым вынут белый шар, В – вторым вынут синий, тогда АВ – вынуты по очереди белый и синий шары. Найдем вероятности: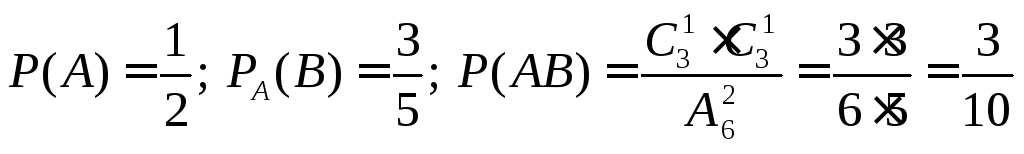. Подста-вив эти вероятности в формулу (1), убеждаемся, что она справедлива.

Определение 2. Если и, то такие события называютсянезависимыми.

Теорема 1. . (2)

Это следует из формулы (1).

Следствие 1. Для независимых событий .

Следствие 2. Если обозначить и, то вероятность появленияхотя бы одного из событий, независимых в совокупности, равна

. (3)

Рассмотрим событие  ни одного не наступило. Тогда по следствию 1 из определения вероятности получаем

.

2.2. Теорема сложения вероятностей

Теорема 2. . (4)

Из диаграммы событий легко получить равенства:

,

где и попарно

несовместные события. А В

Тогда, согласно третьей аксиоме,

получаем

и .

Если из последнего равенства выразить и подставить в первое, то получим формулу (4).

Следствие 3. Если А и В  несовместные события, то получаем третью аксиому.

Пример 2. Вероятности попадания при двух выстрелах соответственно равны . Найти вероятность поражения цели.

Вероятность поражения цели представляет собой событие , где событиеА  поражение цели при первом выстреле, а событие В - поражение при втором выстреле.

Первый способ: По теореме сложения вероятностей получаем

Второй способ: По формуле (3) получаем

.

Пример 3. Устройство содержит три независимо работающих элемента. Вероятности отказа элементов соответственно равны: 0,05 ; 0,06 ; 0,08 . Найти вероятности событий:

1. Откажет один элемент.

Введём события: А - интересующее нас событие; В - отказал первый элемент; С - отказал второй элемент; D - отказал третий элемент.

Тогда

и, согласно теоремам об умножении и сложении вероятностей, получим

2. Ни один элемент не откажет.

Здесь интересующее нас событие и тогда