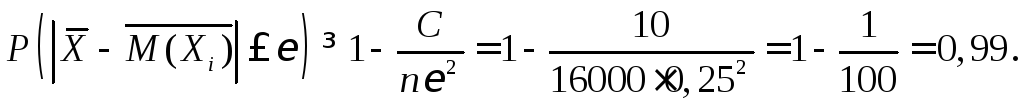- •Курс лекций
- •2. Решение волнового уравнения методом Фурье
- •Кратные интегралы Лекция № 51. Тема 1: Определение кратного интеграла
- •1.1. Задачи, приводящие к понятию кратного интеграла
- •1.2. Определение кратного интеграла и его основные свойства
- •Тема 2: Двойной интеграл
- •2.1. Определение двойного интеграла
- •2.2. Вычисление двойного интеграла.
- •Лекция № 52
- •2.3. Замена переменных в двойном интеграле.
- •2.4. Двойной интеграл в полярной системе координат
- •2.5. Приложения двойного интеграла
- •. Лекция № 53
- •Лекция № 54. Тема 3 : Тройной интеграл
- •3.1. Определение и вычисление тройного интеграла
- •3.2. Замена переменных в тройном интеграле
- •3.3. Приложения тройного интеграла
- •Лекция № 55. Тема 4 : Криволинейные интегралы
- •4.1. Криволинейные интегралы первого рода или по длине дуги
- •4.2. Криволинейные интегралы второго рода или по координатам
- •Лекция № 56.
- •4.3. Формула Грина
- •4.4. Условие независимости криволинейного интеграла второго рода от пути интегрирования
- •Тема 5 : Поверхностные интегралы
- •5.1. Поверхностные интегралы первого рода
- •5.2. Поверхностные интегралы второго рода
- •5.3. Приложения поверхностных интегралов
- •Лекция № 57. Тема 6 : Элементы теории поля
- •6.1. Понятие поля
- •6.2. Формула Гаусса Остроградского
- •6.3. Формула Стокса
- •Теория вероятностей Лекция № 58. Тема 1 : Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •Лекция № 59
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •Лекция № 60. Тема 2 : Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •Лекция № 61. Тема 3 : Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •Лекция № 62. Тема 4 : Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Непрерывная св. Функция распределения
- •Лекция № 63. Тема 5 : Числовые характеристики св
- •5.1. Математическое ожидание св
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Понятие о моментах св
- •Лекция № 64. Тема 6 : Основные законы распределения случайных величин
- •6.1. Дискретные законы распределения
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Непрерывные законы распределения
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •Лекция № 65
- •6.2.3. Нормальное распределение
- •Тема 7 : Закон больших чисел
- •Лекция № 66. Тема 8 : Многомерные случайные величины
- •8.1. Многомерные св и их функции распределения
- •8.2. Числовые характеристики двумерной случайной величины
- •Элементы математической статистики Лекция № 67. Введение
- •1. Предмет математической статистики
- •Тема 1: Статистические законы распределения выборки
- •1.1. Полигон и гистограмма
- •1.2. Эмпирическая функция распределения
- •Тема 2 : Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •Лекция № 68
- •Тема 3 : Проверка статистических гипотез. Критерий согласия Пирсона
- •Тема 4 : Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
- •Теория функций комплексной переменной Лекция № 69. Определение функции комплексной переменной
- •1.1. Комплексные числа и действия над ними
- •1.2. Тригонометрическая и показательная формы записи
- •1.3. Определение функции комплексной переменной
- •Лекция № 70
- •1.3. Предел и непрерывность функции комплексной переменной
- •Тема 2 : Ряды с комплексными членами
- •2.1. Числовые ряды
- •2.2. Степенные ряды
- •2.3. Основные элементарные функции комплексной переменной
- •Лекция № 71. Тема 3 : Производная функции комплексной переменной
- •3.1. Определение производной
- •3.2. Гармонические функции
- •Тема 4 : Интеграл от функции комплексной переменной
- •4.1. Определение интеграла
- •4.2. Основная теорема Коши
- •Лекция № 72
- •4.3. Интегральная формула Коши
- •4.4. Производные высших порядков от аналитической функции
- •4.5. Ряд Тейлора
- •. . . . .
- •4.6. Ряд Лорана
- •Лекция № 73
- •Тема 5 : Вычеты
- •5.1. Изолированные особые точки аналитической функции
- •5.2. Определение вычета
- •5.3. Основная теорема о вычетах
- •5.4. Приложение вычетов к вычислению интегралов
- •Операционное исчисление Лекция № 74. Тема 1 : Оригинал и изображение
- •1.1. Определение оригинала и изображения
- •1.2. Изображения некоторых функций
- •Тема 2 : Основные теоремы операционного исчисления
- •2.1. Теоремы подобия, запаздывания и смещения
- •Лекция № 75.
- •3.2. Приложение операционного исчисления к задачам техники
- •С о д е р ж а н и е
Лекция № 65
6.2.3. Нормальное распределение
Определение 3.
СВ X
называется распределённой по нормальному
закону, если функция плотности
распределения
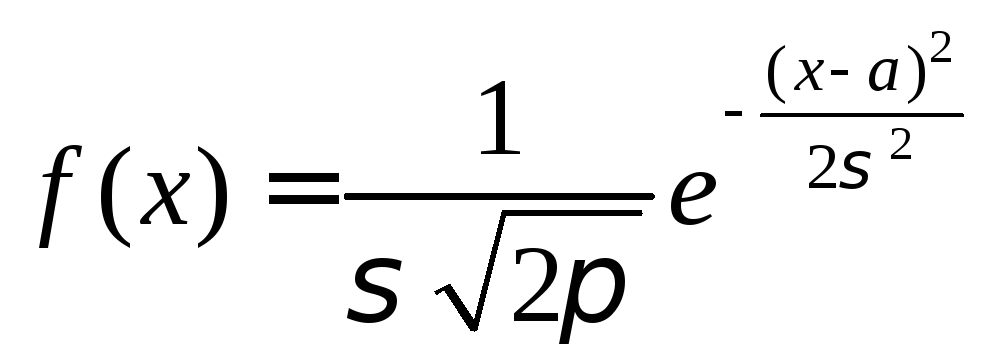 .
.
Определим смысл
параметров a
и
![]() .
Для этого вычислим:
.
Для этого вычислим:
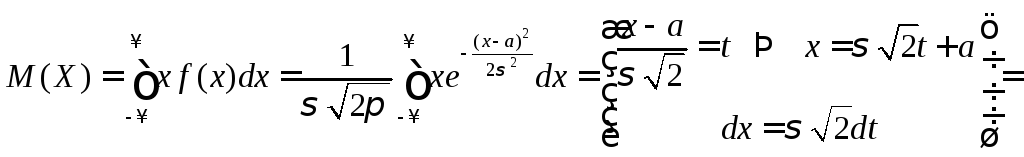
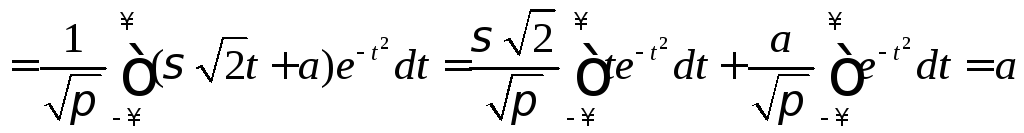 ,
,
так как первый интеграл равен нулю, как интеграл от нечетной функции в симметричных пределах, а второй является интегралом Пуассона.
Таким образом,
![]() .
Аналогично можно показать, что
.
Аналогично можно показать, что![]() ,
т.е.
,
т.е.![]() .
.
График функции нормального распределения имеет вид (Лекция 22)

f(х)
О ![]() а
а
![]() х
х
Здесь
![]() точки
перегиба,
точки
перегиба,
![]() .
.
Если вычислить значения центральных моментов
 ,
,
то получим
![]()
Часто на практике в качестве числовых характеристик используются так называемые эксцесс Ex и коэффициент асимметрии As. В частности, для нормального распределения они равны:
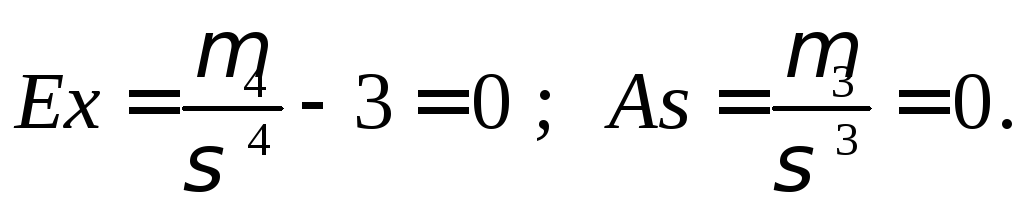
Таким образом, эти коэффициенты определяют степень отклонения распределений от нормального.
Вероятность попадания в заданный интервал случайной величины, имеющей нормальное распределение, определяется по формуле

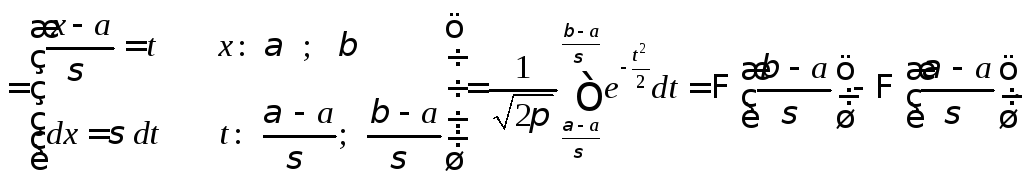 (1)
(1)
Следствие 1.
При
![]() и
и![]() из формулы (1) получаем
из формулы (1) получаем
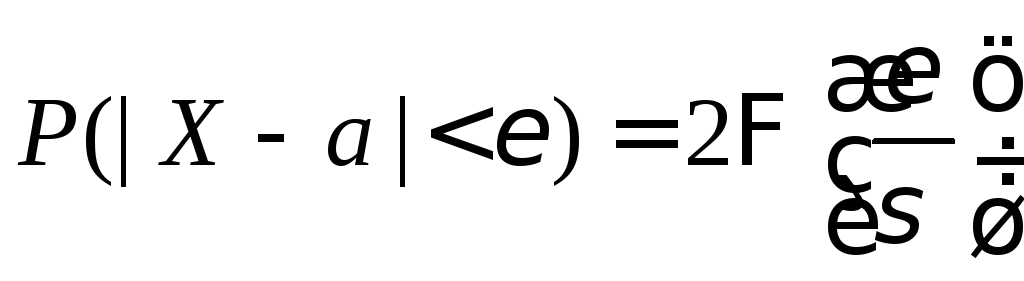 .
(2)
.
(2)
Следствие 2.
Если положить в формуле (2)
![]() и учесть, что при
и учесть, что при![]()
![]() ,
то получим
,
то получим
![]() .
(3)
.
(3)
Выражение (3)
представляет собой так называемое
правило трёх
сигм. Оно
означает, что практически в интервале
![]() находятся все возможные значения
нормально распределённой СВ.
находятся все возможные значения
нормально распределённой СВ.
Нормальный закон распределения играет в теории вероятностей важную роль, так как является предельным законом, к которому приближаются многие другие законы. Это отражено в центральной предельной теореме Ляпунова.
Теорема.
Если Х
сумма большого числа независимых
случайных величин
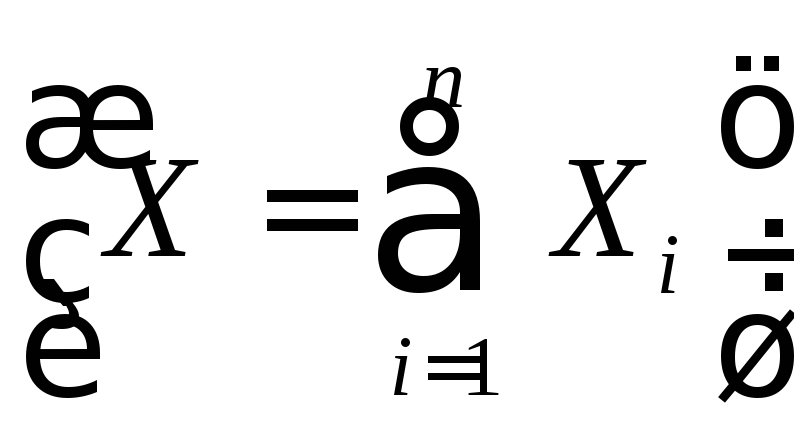 ,
которые имеют различные распределения
и их влияние на СВХ
незначительно, то Х
имеет распределение близкое к нормальному.
А в пределе СВ Х
стремится к нормальному закону.
,
которые имеют различные распределения
и их влияние на СВХ
незначительно, то Х
имеет распределение близкое к нормальному.
А в пределе СВ Х
стремится к нормальному закону.
Нормальный закон широко используется в теории ошибок, в теории стрельбы, теории надёжности и т.д.
Пример 3.
По цели, имеющей вид полосы, ширина
которой 20
м, ведётся стрельба в направлении
перпендикулярном полосе. Прицеливание
ведётся по средней линии. Среднее
квадратическое отклонение (точность
прицела) в направлении стрельбы равна
![]() .
Найти вероятность попадания в цель при
одном выстреле.
.
Найти вероятность попадания в цель при
одном выстреле.
 у
у
10 а = 0 10 х
Здесь
![]()
Подставляя в формулу (2) эти значения, получим
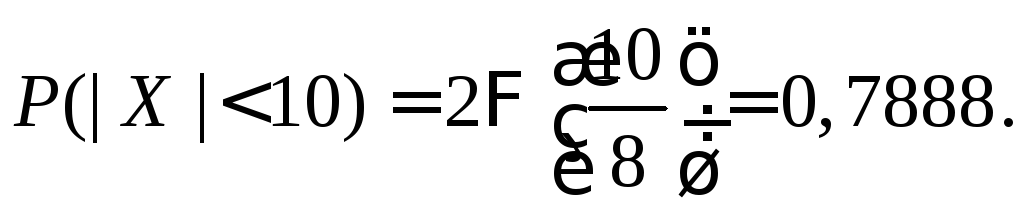
Тема 7 : Закон больших чисел
Этот закон обосновывает устойчивость средних, т.е. при очень большом числе случайных событий их средний результат практически перестаёт быть случайным и может быть предсказан с большой точностью. Какие условия необходимы для этого?
7.1. Неравенство Чебышева
Теорема
1.
Если случайная величина Х
имеет конечную дисперсию, то для
![]() справедливо
неравенство
справедливо
неравенство
 .
.
Доказательство проведём для непрерывной СВ.
Из рисунка

![]()
![]()
![]() х
х
![]()
![]()
![]()
следует
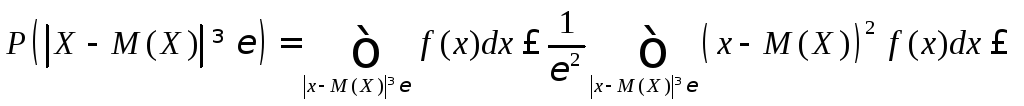
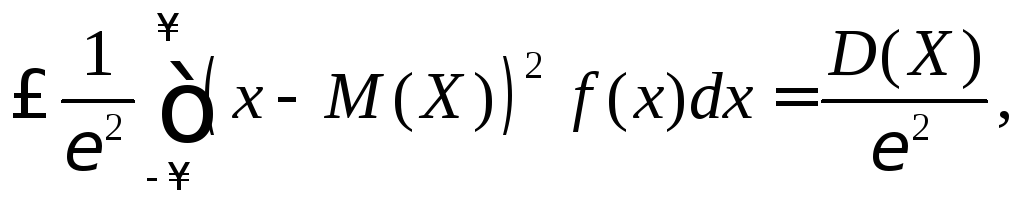
что и требовалось доказать.
Пример 3.
Дана случайная величина Х
с математическим ожиданием
![]() и дисперсией
и дисперсией![]() .
Оценить вероятность того, что случайная
величина Х
отклонится от своего математического
ожидания не менее, чем на
.
Оценить вероятность того, что случайная
величина Х
отклонится от своего математического
ожидания не менее, чем на
![]() .
.
Положим в
неравенстве Чебышева
![]() ,
тогда верхняя граница вероятностей
,
тогда верхняя граница вероятностей
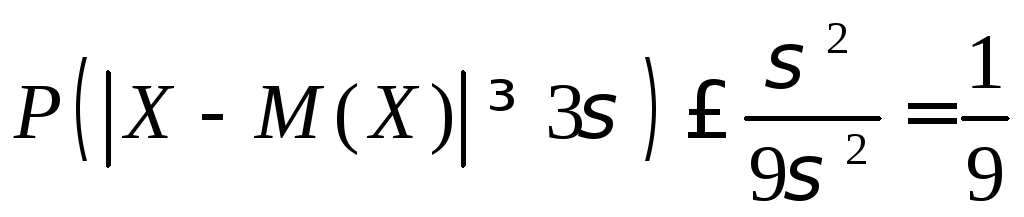 ,
,
что верно для всех законов распределения СВ.
7.2. Теорема Чебышева
Теорема 2.
Если
![]()
независимые СВ, имеющие конечные
дисперсии, т.е.
независимые СВ, имеющие конечные
дисперсии, т.е.
![]() ,
то
,
то![]()
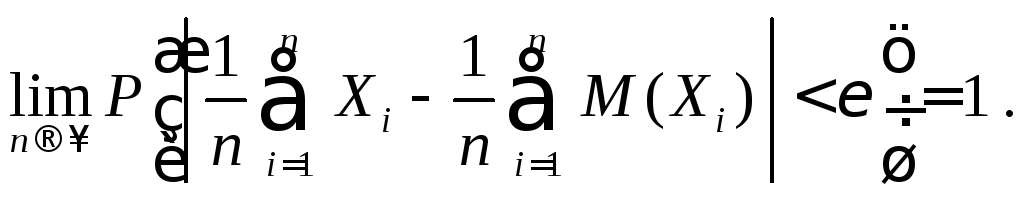
Рассмотрим новую
СВ
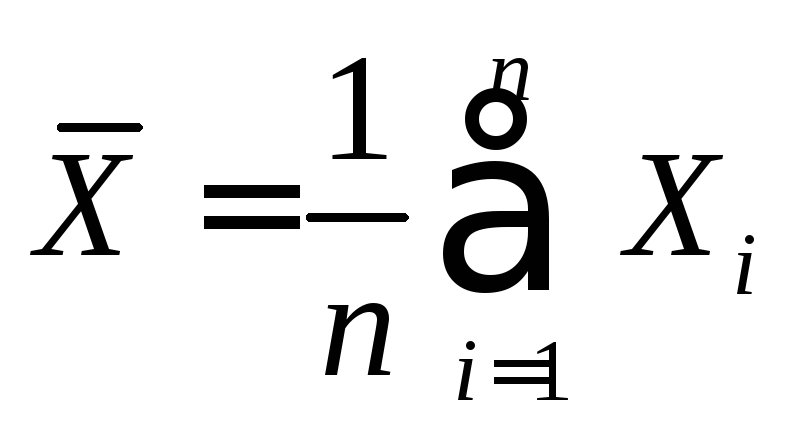 и применим к ней неравенство Чебышева
и применим к ней неравенство Чебышева
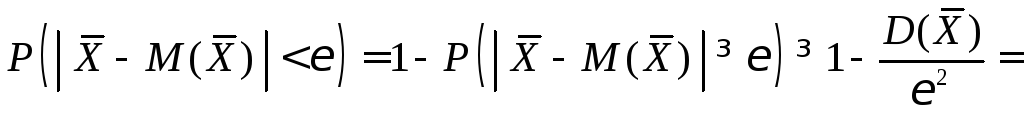
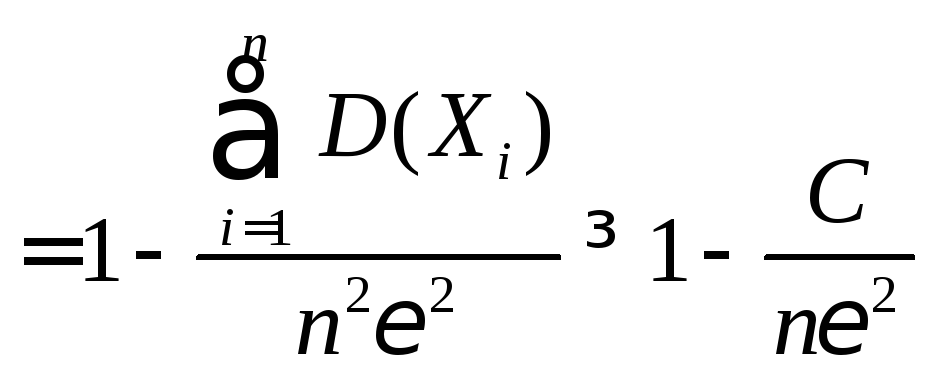 .
.
Переходя к пределу
при
![]() и, учитывая что
и, учитывая что![]() ,
получаем теорему Чебышева.
,
получаем теорему Чебышева.
Следствия:
1.
Теорема
Бернулли.
Если
![]()
число наступления события А
в п
независимых испытаниях, а р
вероятность А,
то
число наступления события А
в п
независимых испытаниях, а р
вероятность А,
то
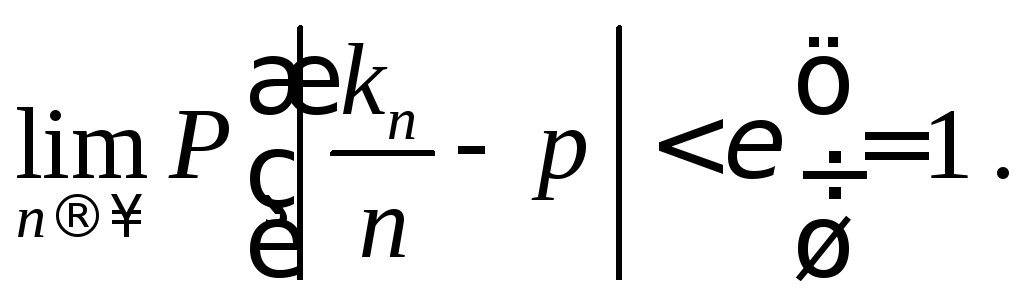
Пусть
![]()
число появления события A
в одном испытании, т.е.
число появления события A
в одном испытании, т.е.
-
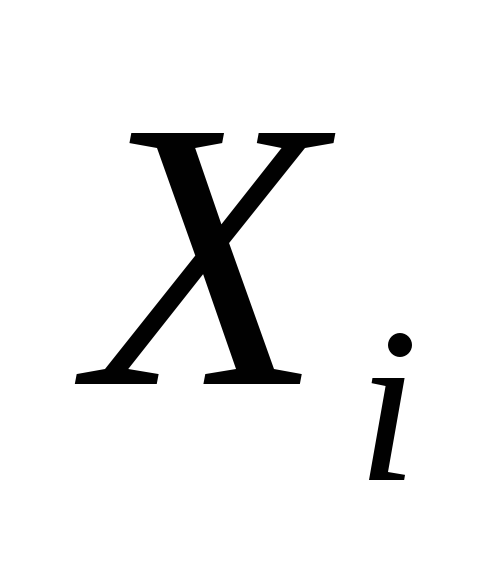
0
1
p
q
p
Тогда
![]() и
и
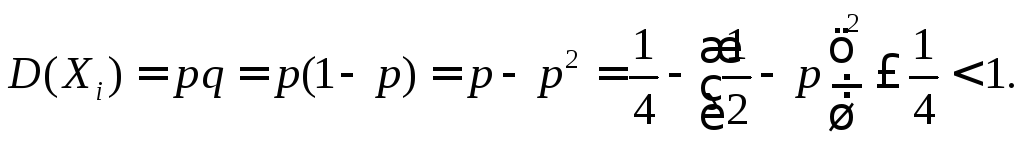
Подставляя в неравенство Чебышева соответствующие значения, полу-чаем теорему Бернулли.
2.
Если для последовательности независимых
случайных величин вы-полняется
равенство
![]() ,
то
,
то
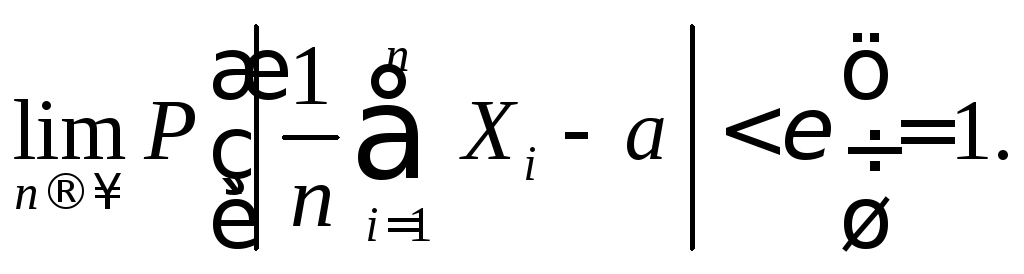
Доказательство следует из теоремы Чебышева.
Этот частный случай
даёт основание правилу среднего
арифметичес-кого, употребляемого в
теории измерений, т.е. если результаты
измерений:
![]() ,
то искомая величина
,
то искомая величина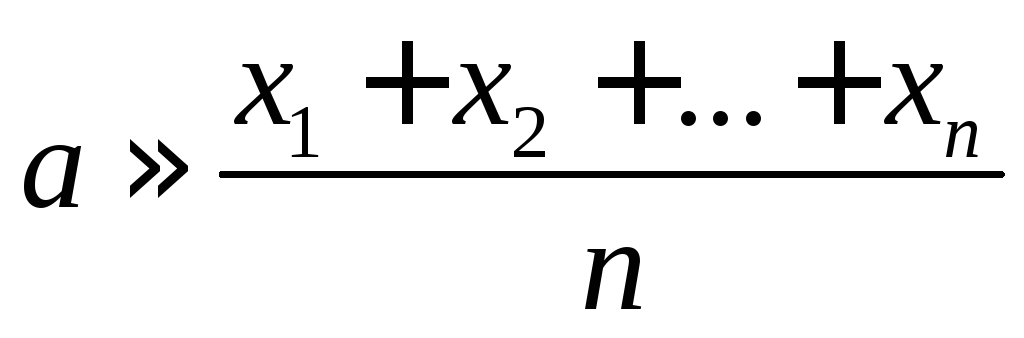 .
Следовательно,
увеличивая число измерений, мы получим
более надежный результат.
.
Следовательно,
увеличивая число измерений, мы получим
более надежный результат.
Пример 3. Дисперсия каждой из попарно независимых случайных величин не превышает 10. Оценить вероятность того, что отклонение среднего арифметического 16000 этих величин от среднего арифметического их математических ожиданий не превосходит 0,25.
По условию
![]()
Тогда по теореме Чебышева С = 10 и искомая вероятность