
- •Курс лекций
- •2. Решение волнового уравнения методом Фурье
- •Кратные интегралы Лекция № 51. Тема 1: Определение кратного интеграла
- •1.1. Задачи, приводящие к понятию кратного интеграла
- •1.2. Определение кратного интеграла и его основные свойства
- •Тема 2: Двойной интеграл
- •2.1. Определение двойного интеграла
- •2.2. Вычисление двойного интеграла.
- •Лекция № 52
- •2.3. Замена переменных в двойном интеграле.
- •2.4. Двойной интеграл в полярной системе координат
- •2.5. Приложения двойного интеграла
- •. Лекция № 53
- •Лекция № 54. Тема 3 : Тройной интеграл
- •3.1. Определение и вычисление тройного интеграла
- •3.2. Замена переменных в тройном интеграле
- •3.3. Приложения тройного интеграла
- •Лекция № 55. Тема 4 : Криволинейные интегралы
- •4.1. Криволинейные интегралы первого рода или по длине дуги
- •4.2. Криволинейные интегралы второго рода или по координатам
- •Лекция № 56.
- •4.3. Формула Грина
- •4.4. Условие независимости криволинейного интеграла второго рода от пути интегрирования
- •Тема 5 : Поверхностные интегралы
- •5.1. Поверхностные интегралы первого рода
- •5.2. Поверхностные интегралы второго рода
- •5.3. Приложения поверхностных интегралов
- •Лекция № 57. Тема 6 : Элементы теории поля
- •6.1. Понятие поля
- •6.2. Формула Гаусса Остроградского
- •6.3. Формула Стокса
- •Теория вероятностей Лекция № 58. Тема 1 : Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •Лекция № 59
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •Лекция № 60. Тема 2 : Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •Лекция № 61. Тема 3 : Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •Лекция № 62. Тема 4 : Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Непрерывная св. Функция распределения
- •Лекция № 63. Тема 5 : Числовые характеристики св
- •5.1. Математическое ожидание св
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Понятие о моментах св
- •Лекция № 64. Тема 6 : Основные законы распределения случайных величин
- •6.1. Дискретные законы распределения
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Непрерывные законы распределения
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •Лекция № 65
- •6.2.3. Нормальное распределение
- •Тема 7 : Закон больших чисел
- •Лекция № 66. Тема 8 : Многомерные случайные величины
- •8.1. Многомерные св и их функции распределения
- •8.2. Числовые характеристики двумерной случайной величины
- •Элементы математической статистики Лекция № 67. Введение
- •1. Предмет математической статистики
- •Тема 1: Статистические законы распределения выборки
- •1.1. Полигон и гистограмма
- •1.2. Эмпирическая функция распределения
- •Тема 2 : Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •Лекция № 68
- •Тема 3 : Проверка статистических гипотез. Критерий согласия Пирсона
- •Тема 4 : Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
- •Теория функций комплексной переменной Лекция № 69. Определение функции комплексной переменной
- •1.1. Комплексные числа и действия над ними
- •1.2. Тригонометрическая и показательная формы записи
- •1.3. Определение функции комплексной переменной
- •Лекция № 70
- •1.3. Предел и непрерывность функции комплексной переменной
- •Тема 2 : Ряды с комплексными членами
- •2.1. Числовые ряды
- •2.2. Степенные ряды
- •2.3. Основные элементарные функции комплексной переменной
- •Лекция № 71. Тема 3 : Производная функции комплексной переменной
- •3.1. Определение производной
- •3.2. Гармонические функции
- •Тема 4 : Интеграл от функции комплексной переменной
- •4.1. Определение интеграла
- •4.2. Основная теорема Коши
- •Лекция № 72
- •4.3. Интегральная формула Коши
- •4.4. Производные высших порядков от аналитической функции
- •4.5. Ряд Тейлора
- •. . . . .
- •4.6. Ряд Лорана
- •Лекция № 73
- •Тема 5 : Вычеты
- •5.1. Изолированные особые точки аналитической функции
- •5.2. Определение вычета
- •5.3. Основная теорема о вычетах
- •5.4. Приложение вычетов к вычислению интегралов
- •Операционное исчисление Лекция № 74. Тема 1 : Оригинал и изображение
- •1.1. Определение оригинала и изображения
- •1.2. Изображения некоторых функций
- •Тема 2 : Основные теоремы операционного исчисления
- •2.1. Теоремы подобия, запаздывания и смещения
- •Лекция № 75.
- •3.2. Приложение операционного исчисления к задачам техники
- •С о д е р ж а н и е
2.3. Формула полной вероятности
Пусть событие А
может наступить при условии появления
одного из событий
![]() ,
образующих полную группу событий. Будем
называть ихгипотезами.
Пусть известны вероятности гипотез:
,
образующих полную группу событий. Будем
называть ихгипотезами.
Пусть известны вероятности гипотез:
![]()
![]() и условные вероятности:
и условные вероятности:![]() .
Тогда имеет место формула полной
вероятности
.
Тогда имеет место формула полной
вероятности
Теорема 3.
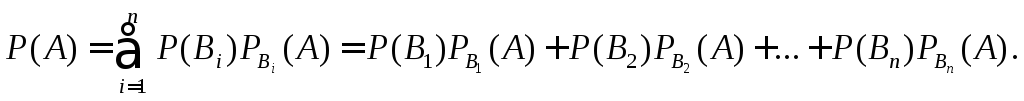 (5)
(5)
Представим событие А в виде
![]() .
.
Так как события
![]() попарно несовместны, т.е.
попарно несовместны, т.е.![]() ,
то и
,
то и![]() .
.
Тогда по третьей аксиоме и теореме умножения вероятностей получим
![]()
![]() .
.
Пример 4. Три станка выпускают одинаковую продукцию. Первый станок выпускает 20%, из них – 5% брака, второй - 30% и 3% брака, третий - 50% и 2% брака. Из общей партии берётся наудачу деталь. Какая вероятность того, что эта деталь бракована?
Пусть А - интересующее нас событие, в качестве гипотез рассмотрим события:
![]() - деталь изготовлена
на первом станке,
- деталь изготовлена
на первом станке,
![]()
![]() - деталь изготовлена
на втором станке,
- деталь изготовлена
на втором станке,
![]()
![]() - деталь изготовлена
на третьем станке,
- деталь изготовлена
на третьем станке,
![]()
Тогда по формуле (5) получим
![]()
![]()
2.4. Формула Бейеса
Условия такие же, как и для формулы полной вероятности. Пусть событие А произошло, тогда вероятности гипотез могут быть переоценены по формуле Бейеса.
Теорема 4.
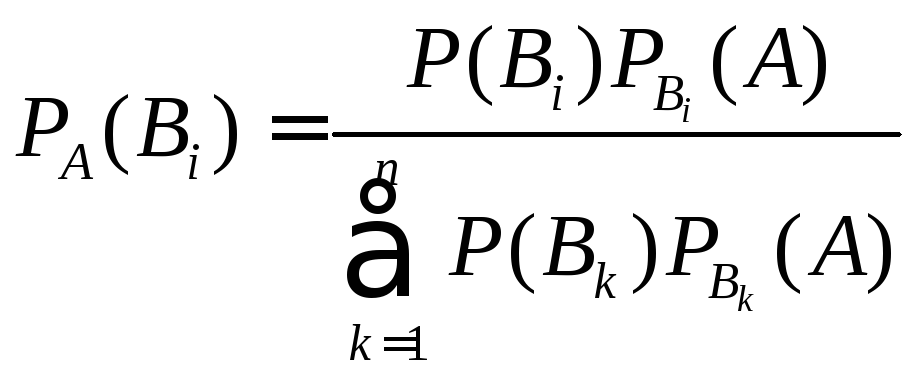 .
(6)
.
(6)
По теореме умножения вероятностей имеем
![]()
или, с учетом формулы полной вероятности, получаем
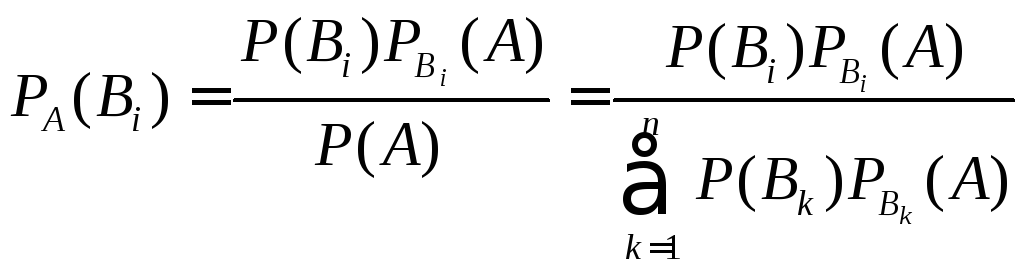 .
.
Пример 5. Число грузовых автомашин, проезжающих по шоссе, на котором находится бензоколонка, относится к числу легковых как 3:2. вероятность того, что будет заправляться грузовая равна 0,1, легковая – 0,2. К заправке подъехала машина. Найти вероятность того, что она грузовая.
Введём гипотезы:
![]() - подъехала грузовая
машина,
- подъехала грузовая
машина,
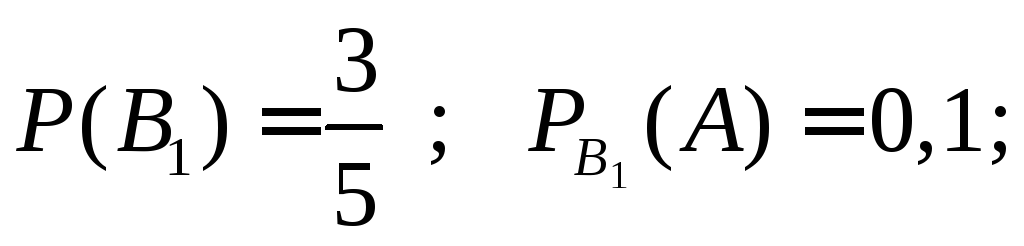
![]() - подъехала легковая
машина,
- подъехала легковая
машина,
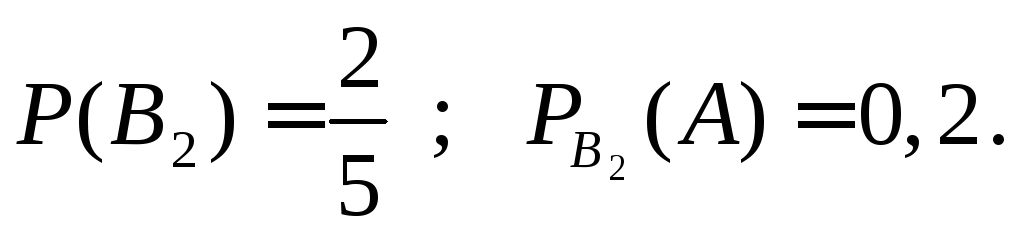
Тогда по формуле (6) получаем
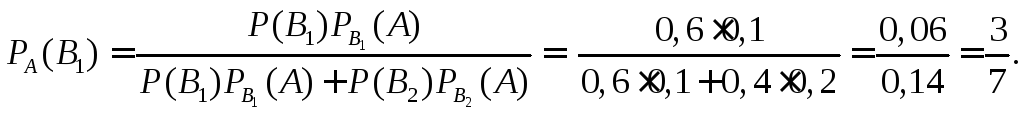
Лекция № 61. Тема 3 : Повторение испытаний
3.1. Независимые испытания. Формула Бернулли
Испытание – это
осуществление определённых условий, в
результате которых может произойти
то или иное элементарное событие
простран-ства E.
Если число исходов испытания - m,
то назовём событие
![]()
i-м
исходом
i-м
исходом
![]() .
Обозначим
.
Обозначим![]() и будем считать, что все
и будем считать, что все
события
![]() образуют полную группу событий, тогда
образуют полную группу событий, тогда
Пусть произведено n испытаний.
Определение 1. Если исходы испытания в каждом опыте не зависят от предыдущих исходов, то такие испытания называются независимыми.
Например, при бросании игральной кости, исходы: выпало одно, два очка и т.д. не зависят от предыдущих очков – испытания независимые.
Рассмотрим случай
![]() (схема Бернулли). Положим
(схема Бернулли). Положим![]()
![]() ,
т.е.
,
т.е.![]() .
.
Рассмотрим
следующую задачу. Пусть произведено n
независимых испытаний, в каждом из
которых событие A
может появиться с одной и той же
вероятностью р.
Требуется найти
![]()
вероятность того, что событие А
появится k
раз, а событие
вероятность того, что событие А
появится k
раз, а событие
![]() появится
появится![]() раз.
раз.
Рассмотрим в какой
либо последовательности чередование
событий А
и
![]() так, чтобыА
повторялось k
раз, а событие
так, чтобыА
повторялось k
раз, а событие
![]() появилось
появилось![]() раз. Это событие
раз. Это событие![]() .
По теореме умножения вероятностей
получаем
.
По теореме умножения вероятностей
получаем
![]() .
.
По теореме сложения
вероятностей
![]() равна сумме таких вероятностей для всех
различных способов появлений событияА
(k
раз из п),
т.е. их число
равна сумме таких вероятностей для всех
различных способов появлений событияА
(k
раз из п),
т.е. их число
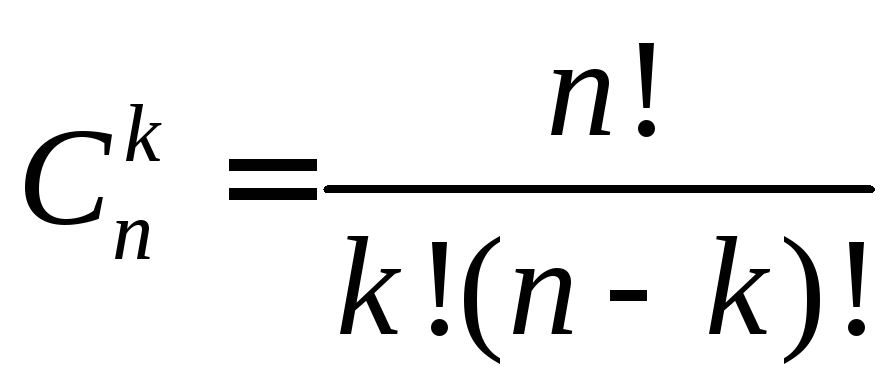 .
Поскольку все эти вероятности равны,
то получаем формулу Бернулли
.
Поскольку все эти вероятности равны,
то получаем формулу Бернулли
 .
(1)
.
(1)
Замечание 1.
Так как все возможные исходы:
событие А
появилось 0
раз, 1
раз, …
, п
раз образуют полную группу событий,
то
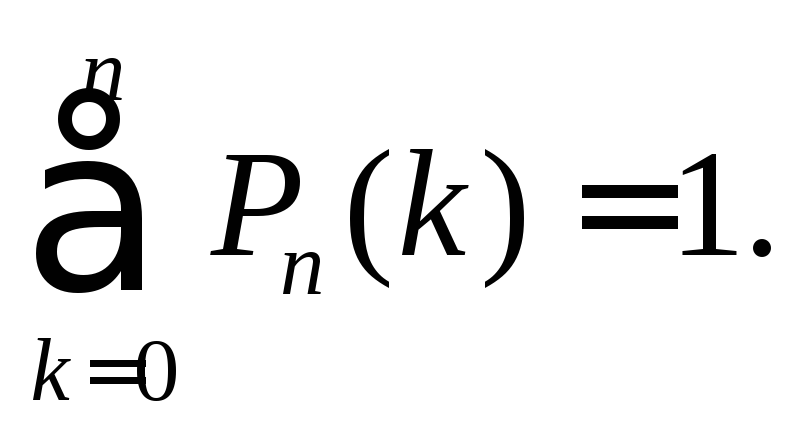
Пример 1. Вероятность хотя бы одного попадания при двух выстрелах равна 0, 96. Найти вероятность трёх попаданий при четырёх выстрелах.
Если
![]()
вероятность хотя бы одного попадания
при двух выст-релах, то
вероятность хотя бы одного попадания
при двух выст-релах, то
![]() ,
,
тогда вероятность
одного попадания
![]() и вероятность трёх попаданий при
четырёх выстрелах
и вероятность трёх попаданий при
четырёх выстрелах

