
- •Курс лекций
- •2. Решение волнового уравнения методом Фурье
- •Кратные интегралы Лекция № 51. Тема 1: Определение кратного интеграла
- •1.1. Задачи, приводящие к понятию кратного интеграла
- •1.2. Определение кратного интеграла и его основные свойства
- •Тема 2: Двойной интеграл
- •2.1. Определение двойного интеграла
- •2.2. Вычисление двойного интеграла.
- •Лекция № 52
- •2.3. Замена переменных в двойном интеграле.
- •2.4. Двойной интеграл в полярной системе координат
- •2.5. Приложения двойного интеграла
- •. Лекция № 53
- •Лекция № 54. Тема 3 : Тройной интеграл
- •3.1. Определение и вычисление тройного интеграла
- •3.2. Замена переменных в тройном интеграле
- •3.3. Приложения тройного интеграла
- •Лекция № 55. Тема 4 : Криволинейные интегралы
- •4.1. Криволинейные интегралы первого рода или по длине дуги
- •4.2. Криволинейные интегралы второго рода или по координатам
- •Лекция № 56.
- •4.3. Формула Грина
- •4.4. Условие независимости криволинейного интеграла второго рода от пути интегрирования
- •Тема 5 : Поверхностные интегралы
- •5.1. Поверхностные интегралы первого рода
- •5.2. Поверхностные интегралы второго рода
- •5.3. Приложения поверхностных интегралов
- •Лекция № 57. Тема 6 : Элементы теории поля
- •6.1. Понятие поля
- •6.2. Формула Гаусса Остроградского
- •6.3. Формула Стокса
- •Теория вероятностей Лекция № 58. Тема 1 : Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •Лекция № 59
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •Лекция № 60. Тема 2 : Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •Лекция № 61. Тема 3 : Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •Лекция № 62. Тема 4 : Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Непрерывная св. Функция распределения
- •Лекция № 63. Тема 5 : Числовые характеристики св
- •5.1. Математическое ожидание св
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Понятие о моментах св
- •Лекция № 64. Тема 6 : Основные законы распределения случайных величин
- •6.1. Дискретные законы распределения
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Непрерывные законы распределения
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •Лекция № 65
- •6.2.3. Нормальное распределение
- •Тема 7 : Закон больших чисел
- •Лекция № 66. Тема 8 : Многомерные случайные величины
- •8.1. Многомерные св и их функции распределения
- •8.2. Числовые характеристики двумерной случайной величины
- •Элементы математической статистики Лекция № 67. Введение
- •1. Предмет математической статистики
- •Тема 1: Статистические законы распределения выборки
- •1.1. Полигон и гистограмма
- •1.2. Эмпирическая функция распределения
- •Тема 2 : Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •Лекция № 68
- •Тема 3 : Проверка статистических гипотез. Критерий согласия Пирсона
- •Тема 4 : Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
- •Теория функций комплексной переменной Лекция № 69. Определение функции комплексной переменной
- •1.1. Комплексные числа и действия над ними
- •1.2. Тригонометрическая и показательная формы записи
- •1.3. Определение функции комплексной переменной
- •Лекция № 70
- •1.3. Предел и непрерывность функции комплексной переменной
- •Тема 2 : Ряды с комплексными членами
- •2.1. Числовые ряды
- •2.2. Степенные ряды
- •2.3. Основные элементарные функции комплексной переменной
- •Лекция № 71. Тема 3 : Производная функции комплексной переменной
- •3.1. Определение производной
- •3.2. Гармонические функции
- •Тема 4 : Интеграл от функции комплексной переменной
- •4.1. Определение интеграла
- •4.2. Основная теорема Коши
- •Лекция № 72
- •4.3. Интегральная формула Коши
- •4.4. Производные высших порядков от аналитической функции
- •4.5. Ряд Тейлора
- •. . . . .
- •4.6. Ряд Лорана
- •Лекция № 73
- •Тема 5 : Вычеты
- •5.1. Изолированные особые точки аналитической функции
- •5.2. Определение вычета
- •5.3. Основная теорема о вычетах
- •5.4. Приложение вычетов к вычислению интегралов
- •Операционное исчисление Лекция № 74. Тема 1 : Оригинал и изображение
- •1.1. Определение оригинала и изображения
- •1.2. Изображения некоторых функций
- •Тема 2 : Основные теоремы операционного исчисления
- •2.1. Теоремы подобия, запаздывания и смещения
- •Лекция № 75.
- •3.2. Приложение операционного исчисления к задачам техники
- •С о д е р ж а н и е
3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
Пусть производится
п
независимых испытаний с постоянной
вероят-ностью р.
Требуется найти вероятность того, что
отклонение частоты
![]() отр
по абсолютной величине не превосходит
данного
отр
по абсолютной величине не превосходит
данного
![]() ,
т.е.
,
т.е.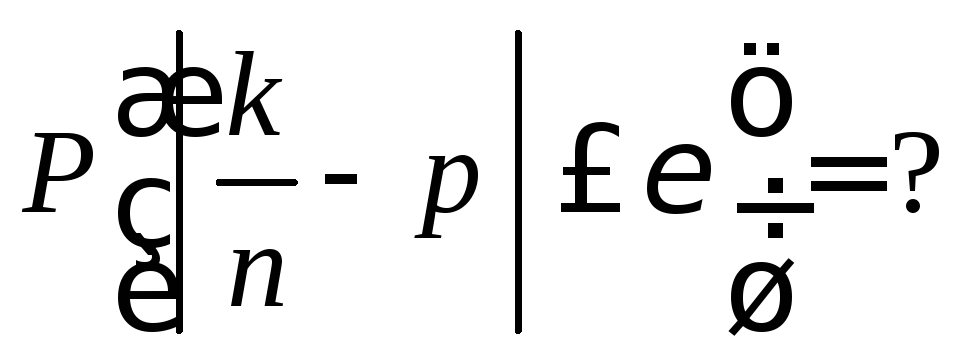
Преобразуем неравенство в скобках

и умножим полученное
неравенство на
![]()

Полагая в формуле
(3)
 и учитывая нечетность функции Лапласа,
получаем
и учитывая нечетность функции Лапласа,
получаем
 .
(5)
.
(5)
Пример 6.
Вероятность появления события А
в каждом из независимых испытаний равна
0,2.
Найти число испытаний п,
при котором с вероят-ностью 0![]() ,9876
можно ожидать, что
,9876
можно ожидать, что
![]()
Подставим данные задачи в формулу (5)

По таблице значений
функции Лапласа
![]() находим соответствующее значение
аргумента
находим соответствующее значение
аргумента
Лекция № 62. Тема 4 : Случайные величины и функции распределения
4.1. Случайные величины
Определение 1.
Случайной величиной (СВ) называется
величина Х,
которая в результате опыта может принять
то или иное значение, заранее неизвестно
какое, т.е.
![]() ,
гдее
элементарное событие.
,
гдее
элементарное событие.
СВ бывают двух типов:
1. Дискретные – если возможные значения СВ (значения, которые она принимает) могут быть перечислены. Например, число попаданий в мишень при п выстрелах, число вызовов на АТС и т.д.
2. Непрерывные – если возможные значения СВ непрерывно заполняют некоторый промежуток. Например, расстояние от точки попадания до центра мишени, время безотказной работы блока устройства.
Для того, чтобы задать СВ, необходимо знать её возможные значения и как часто она их принимает, т.е. с какой вероятностью. Для дискретных СВ закон распределения обычно задается в виде таблицы
|
X |
|
|
… |
|
… |
|
P |
|
|
… |
|
… |
Замечание.
Так как события
![]() образуют полную группу событий, то
образуют полную группу событий, то![]() .
.
Рассмотрим примеры наиболее распространённых дискретных СВ.
1. Биномиальное распределение.
|
X |
0 |
1 |
… |
k |
… |
n |
|
p |
|
|
… |
|
… |
|
2. Распределение Пуассона.
|
X |
0 |
1 |
… |
n |
… |
|
p |
|
|
… |
|
… |
Пример 1. Монета брошена три раза. Построить закон распределения СВ – число появлений герба.
Здесь
![]() .
По формуле Бернулли вычислим
соответст-вующие вероятности:
.
По формуле Бернулли вычислим
соответст-вующие вероятности:
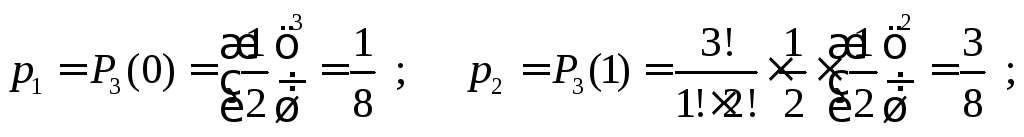
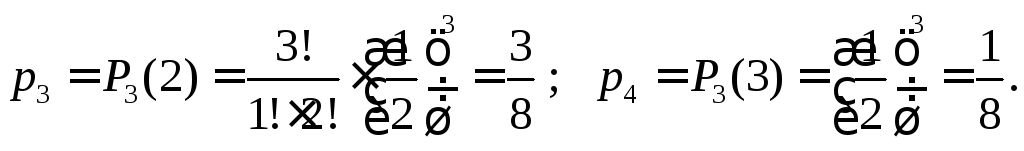
Проверим
 .
.
Получили закон распределения
|
X |
0 |
1 |
2 |
3 |
|
p |
|
|
|
|
4.2. Функция распределения вероятностей для дискретной св
Для количественной
характеристики распределения вероятностей
удобно пользоваться не вероятностью
события
![]() ,
а вероятностью события
,
а вероятностью события![]() .
.
Определение 2.
Функция
![]() называется функцией распределения
вероятностей случайной величиныХ
или интегральной функцией распределения.
называется функцией распределения
вероятностей случайной величиныХ
или интегральной функцией распределения.
Геометрически это
означает, что
![]()
вероятность того, что СВ примет значение,
лежащее левее х.
вероятность того, что СВ примет значение,
лежащее левее х.
Пример 2.
Построить функцию
![]() распределения вероятностей для примера1.
распределения вероятностей для примера1.
1.
![]() ,
для таких значений
,
для таких значений![]() .
.
2.
![]() ,
для таких значений
,
для таких значений .
.
3.
![]() ,
для таких значений
,
для таких значений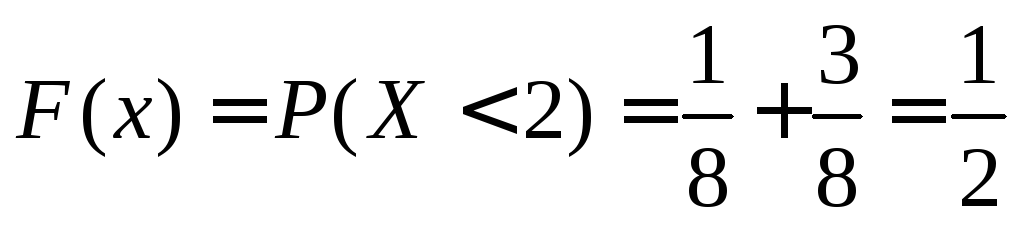 .
.
4.
![]() ,
для таких значений
,
для таких значений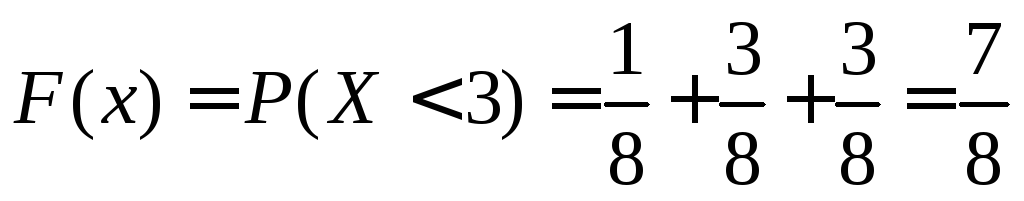 .
.
5 .
.
![]() ,
для таких значений
,
для таких значений .
.
![]()
1
0,5
0 1 2 3 4 х
Из определения функции распределения следуют её свойства:
1.
![]()
2.
![]() - неубывающая функция.
- неубывающая функция.
3.
![]() .
.
4.
Вероятность того, что СВ примет
значение, заключенное в интер-вале
![]() ,
равно
,
равно![]() .
.
Рассмотрим события
![]() ,
тогда
,
тогда![]() .
Так как А
и С
несовместные события,
то
.
Так как А
и С
несовместные события,
то
![]() .
Тогда
учитывая, что
.
Тогда
учитывая, что
![]()
![]() ,
получим
,
получим![]() .
.
5.
![]() имеет разрывы первого рода во всех
точках, соответству-ющих возможным
значениям СВ, а величина скачка равна
имеет разрывы первого рода во всех
точках, соответству-ющих возможным
значениям СВ, а величина скачка равна
![]() .
.


