II Окремі випадки. Важливі поняття

А) Границя на нескінченності ().

Означення 2.

.

Аналогічне означення й для .

Приклад 3. ,.Розглянемо . Тоді для послідовності значень функціїбудемо мати:, тому що н.в., а  обмежена, виходить , тобто. Це означає, що.

Неважко переконатися, що й . Для тих функцій, для яких, можна писати. Навпроти, писатине можна, тому що, а.

Геометрична ілюстрація: скінчена границя функції на означає наявністьу графіка функції горизонтальної асимптоти на (на).

В) Нескінченно малі функції ().

Означення 3. Функцію називають нескінченномалої (н.м.) у точці (або: при) і пишуть «при», якщо, тобто

.

Наприклад, у попередньому пункті ми показали, що при.

Основний результат дає наступна теорема.

Теорема 1. Функція має вточці границютоді й тільки тоді, колирізниця єн.м. при :

при .

С) Нескінченно великі функції ().

Означення 4. Функцію називають нескінченновеликою (н.в.) у точці (при), якщоабо, тобто

н.в. послідовність визна-ченого знака.

Всі властивості н.м. і н.в. послідовностей залишаються справедливими й для н.м. і н.в. функцій. Приведемо лише деякі з них.

Теорема 2. Для того, щоб функція була нескінченновеликою у точці необхідно й достатньо, щоб функціябула нескінченномалої в цій же точці.

І дві властивості.

1) Якщо при, а обмежена в деякому околі точки , тодобуток при.

2) Якщо  н.в. у точці , атака, що, тодобуток єн.в. функція при .

Наприклад, уточці , а многочленєн.в. на , тому що

.

Еталонні н.в. і н.м. функції приведемо в таблиці.

б.м
б.б.

Так само як і н.в. послідовності, н.в. функції можна впорядкувати по їхньому порядку росту: при

.

III Однобічні границі

Розглянемо функцію . Для довільноїн.м. послідовності додатних чиселрозглянемо послідовність . Якдобуток обмеженої на н.м., вона збігається до нуля. Відповідна послідовність значень функції не має грани-ці. Це означає, щоне існує. Однак,імаємо, а дляй .

Така ситуація характерна для багатьох функцій, у яких немає границі в якій-небудь точці, що й привело до появи поняття односторонніх границь.

Означення 5. Нехай

.

Тоді число називають правою границею (границею праворуч або правобічною границею) функціївточці й пишуть:або.

Визначення лівої границі аналогічно, тільки вимогу заміняють вимогою. Позначення:

або .

Якщо , то іноді замістьпишуть. Наприклад,,.

Сформулюємо теорему, на якій базується використання однобічних границь.

Теорема 3. Для існування границі необхідно й достатньо існування порізно й рівність однобічних границь:

.

IV Теореми про границі функцій

Теорема 4. Нехай у функції існує. Тоді в деякомуоколі точки (за винятком, може бути, самоїточки ).Більш того, .

Теорема 5. Нехай у функції існує скінчена границя при. Тоді в деякомуоколі точки функціяобмежена.

Теорема 6. Функція має границю в кожнійточці числової прямої, причому .

Теорема 7 (операції над границями). Нехай функції ймають уточці скінчені границійвідповідно. Тоді в ційточці мають скінчені границі й функції: 1) ; 2); 3); 4); 5)(при). При цьому мають місце наступні рівності:

,

(тут  символ арифметичної операції).

Для доведення розглянемо  довільну послідовність значень аргументу, що збігається до .

Завдяки існуванню границь функцій івідповідні послідовності значень функційімають межій. Тоді, використовуючи теорему 2 §7,одержимо, що послідовність збігається до. Відповідно до визначення границі функції це означає, що.

Теорема 8 (граничний перехід у нерівностях). Нехай функції ймають уточці скінчену границю й у деякомуоколі цієї точки (за винятком, бути може, самої точки) . Тоді й. Зокрема, якщо(), то й().

Теорема 9. Якщо й у деякомуоколі точки (за винятком, бути може, самоїточки) , то.

Теорема 10 (про заміну змінної). Нехай хоча б одна з функцій абоє строго монотонною й нехай існують границі й. Тоді йу складної функції існує границя вточці , причому.

Теорема 11 (границі елементарних функцій). Нехай  елементарна функція й точка разомз деяким околом. Тоді (завдяки неперервності елементарних функцій).

Теорема 12. Усяка обмежена монотонна на проміжку функція має в кожній точці проміжку скінчені односторонні границі.

Приклад 4.

,

.

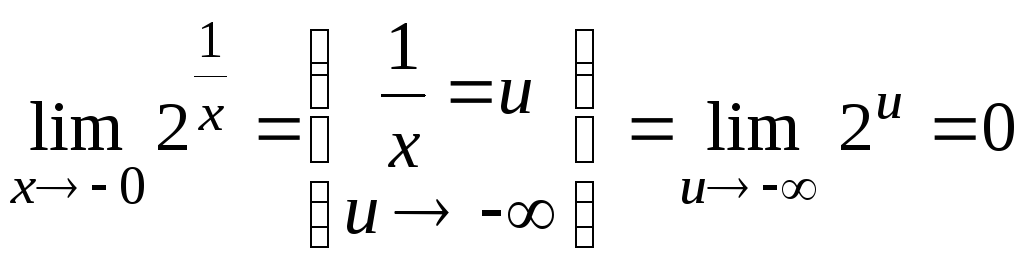Приклад 5.

а) ; б).

Шляхом ділення чисельника й знаменника на самий швидкозростаючий доданок, перейдемо від н.в. функцій до н.м. функцій і одержимо результат:

а) ;

б) .

Зауваження. Крім означення границі функції на «мові послідовнос-тей», існує (рівносильне) визначення границі функції на т.зв. «мові ».Деякі з теорем про границі зручніше доводити саме на цій мові.