104

Тема дослідження функцій за допомогою похідних

Лекція 12

§1. Умова сталості функції

Теорема. Якщо функція неперервна на проміжку й у всіх внутрішніх точках відрізка , то постійна на цьому проміжку.

Доведення. Нехай . Застосуємо теорему Лагранжа до функції на проміжку : . Але за умовою , отже, і тому (на правому кінці через те, що функція неперервна).

Приклад. Розглянемо функцію на проміжку

. Її похідна:

Отже, const на . Щоб знайти цю константу, достатньо обчислити в будь-якій точці, наприклад, . Отже, ми довели тотожність .

В інтегральному численні важливе застосування знайде наслідок, що випливає з доведеної теореми.

Наслідок. Якщо функції й неперервні на проміжку й мають рівні похідні у всіх внутрішніх точках проміжку, то ці функції всюди у відрізняються лише на постійну: .

Для доведення досить застосувати теорему до допоміжної функції . Тоді й .

§2. Умова монотонності функції

Відомо, що функція називається строго зростаючої на , якщо для будь-яких точок з нерівності витікає нерівність . Іншими словами, знак приросту функції збігається зі знаком приросту аргументу: . Для спадної функції, природно, .

Теорема. (Достатня умова монотонності). Нехай функція диференційована на . Тоді:

1) якщо на , то строго зростає на ;

2) якщо на , то строго спадає на .

Доведення. Візьмемо дві довільні точки , причому нехай . Застосуємо теорему Лагранжа до функції на проміжку (умови теореми виконані, тому що неперервність випливає з її диференційованості): По припущенню , отже, знак визначається знаком похідної. 1) Якщо , то й і ; через те, що це вірно для будь-яких , то зростає на . 2) Якщо , то й і , що означає спадання .

Зауваження. Зв'язок між знаком і напрямком зміни геометрично очевидний, якщо згадати, що похідна – це кутовий коефіцієнт дотичноъ до графіка . Однак, навіть у строго монотонної функції дотична може бути й горизонтальною, тобто для окремих значень може обертатися в 0. Прикладом слугує функція : вона строго зростає, але похідна при дорівнює нулю.

Таким чином, теорема зводить питання про зростання (спадання) функції до розв‘яування нерівності ( ).

Приклад. Дослідити на монотонність функцію . Знаходимо похідну й розкладаємо її на множники: . Метод інтервалів дозволяє визначити знак :

-

На інтервалах і функція зростає, а на – спадає.

§3. Дослідження функції на екстремум

Нагадаємо вже відомі факти. По-перше, точка екстремуму – це завжди внутрішня точка області визначення функції; вона характеризується тим, що знак приросту функції не залежить від знака приросту аргументу, якщо останнє достатньо мале. По-друге, необхідна умова екстремуму дається теоремою Ферма: якщо в точці екстремуму функція диференційована (тобто має скінчену похідну), то похідна в цій точці дорівнює 0.

Точки, у яких похідна функції обертається в нуль, прийнято називати стаціонарними точками.

Однак, якщо розглядати функції, що не мають в окремих точках скінченої двосторонньої похідної, то не виключена можливість, що екстремум прийде на на яку-небудь із таких точок. Наприклад, функції й мають у мінімуми, у той же час , і , .

Означення. Точку називають критичною точкою першого порядку функції , якщо або не існує.

З теореми Ферма випливає, що точки екстремуму варто шукати серед критичних точок (їх ще називають точками можливого екстремуму). Потрібне додаткове дослідження таких точок, щоб відібрати серед них точки екстремуму. Це дослідження виконується за допомогою достатніх умов екстремуму.

Теорема 1 (перша достатня умова екстремуму). Нехай – критична точка першого порядку неперервної функції й нехай існує таке, що в однобічних околах цієї точки: і – функція диференційована і її похідна зберігає знак. Тоді:

1) якщо в и в , то – точка максимуму;

2) якщо в и в , то – точка мінімуму;

3) якщо одного знака в і , то в точці немає екстремуму.

Доведення. 1) Візьмемо довільні точки й і розглянемо функцію на двох проміжках: і . На кожному із цих проміжків функція задовольняє умовам теореми Лагранжа, отже, існують точки й такі, що:

,

.

Із цих нерівностей випливає, що й . У такий спосіб, значення – найбільше серед значень для . Це й означає: – точка максимуму.

2) Доводиться аналогічно.

3) Якщо , те зростає як в , так і в. Якщо ж , те спадає в тих же околах. В обох випадках таке поводження функції говорить про те, що не є точкою екстремуму.

Зауваження 1. Вимогу неперервності функції не можна послабити, про що свідчить малюнок: у точці функція має максимум, у той же час при переході через цю точку похідна не змінює знак.

Зауваження 2. Доведену теорему не завжди можна застосувати, тому що для деяких функцій вимога збереження знака похідної не виконується. Наприклад, для функції

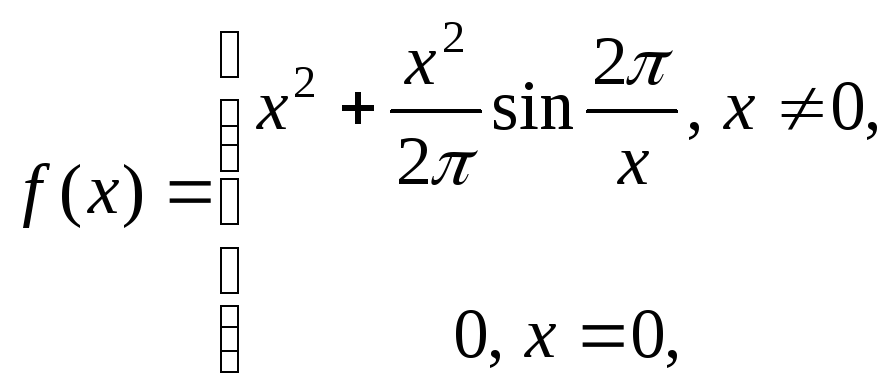
маємо:

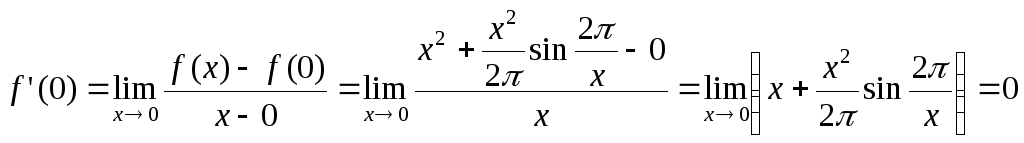, виходить, точка 0 – критична. Далі, для

Вираз в дужках обмежен, тому при близьких до нуля перший член отриманої різниці також близький до нуля, а другий член приймає значення від –1 до +1. Виходить, знак визначається членом . Але в точках виду цей член обертається в нуль і змінює знак. А тому що при , то в будь-якому як завгодно малому околі нуля нескінченне число раз змінює знак.

Теорема 2 (друга достатня умова екстремуму). Нехай функція має в критичній точці скінчену другу похідну. Тоді:

1) якщо , то – точка мінімуму;

2) якщо , то – точка максимуму;

3) якщо , то потрібне додаткове дослідження.

Доведення. Існування скінченої похідної означає, що існує скінчена похідна в деякому околі точки й , тому що – критична точка. Позначимо . Тоді умови теореми означають, що існує скінчена границя

.

Нехай, наприклад, . Тоді для близьких до і , тобто . Це означає, що функція зростає в деякому околі точки . Але . Отже, лівіше точки функція від‘ємна, а правіше – додатна. Однак, . Виходить, перша похідна даної функції при переході через точку змінює знак з «–» на «+». Це означає, що точка – точка мінімуму. Аналогічно розглядається й випадок . У необхідності додаткового дослідження, коли , переконують дві функції: і . Очевидно, що – точка 0 критична для обох функцій, і . Однак, для нуль – це точка мінімуму, а в нулі не має екстремуму.

Зауваження 3. У темі «Формули Тейлора й Маклорена» буде сформульована й доведена третя достатня умова екстремуму, за допомогою якого й виконується це додаткове дослідження.

Приклад 1. Знайти точки екстремуму функції .

Розв‘язування. Розкриємо знак модуля й обчислимо похідну:

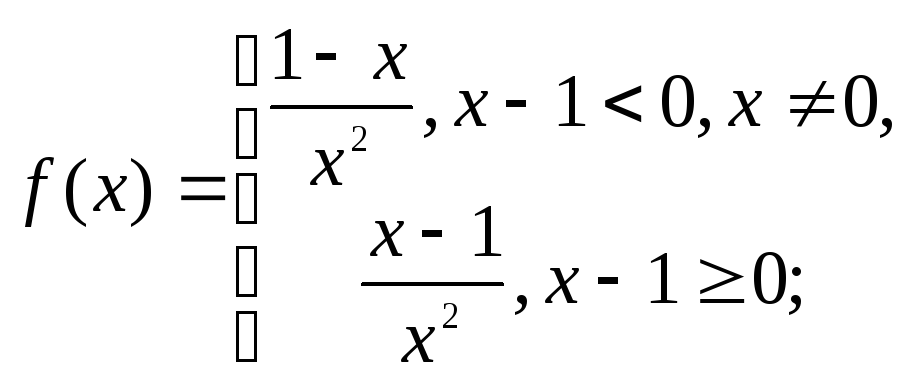
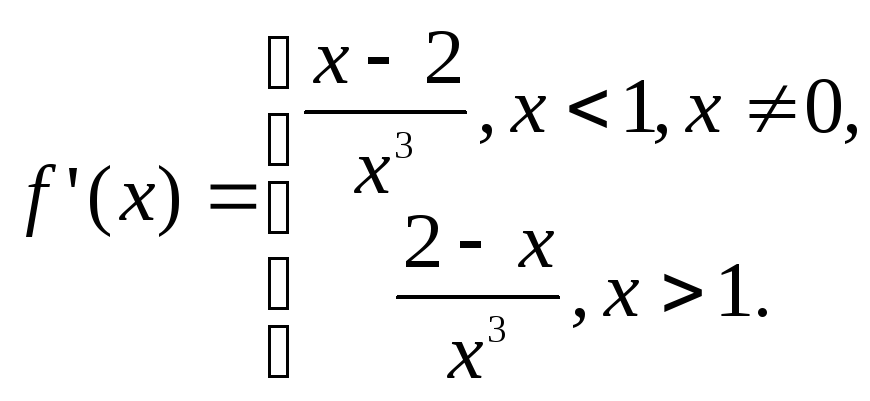
Наявність модуля у виразі для може привести, і в нашім випадку приводить, до неіснування в точці, де модуль обертається в нуль. Дійсно,

Відмінність лівої похідної від правої й означає відсутність похідної в точці , тобто ця точка – критична. Інші критичні точки – це нулі похідної:

Отже, маємо дві критичні точки Вони розбивають область визначення функції на інтервали знакопостійності похідної, тобто на інтервали монотонності функції. Для визначення знака на інтервалі досить визначити цей знак у якій-небудь точці інтервалу. Подальше дослідження зручно вести, намалювавши допоміжне креслення:

Ще раз нагадаємо, що критичні точки наносяться на область визначення. Ми одержуємо 4 інтервали. Визначаємо знаки :

Аналіз креслення показує: у точці функція має локальний мінімум, причому , а в точці – локальний максимум: .

На кресленні бачимо й інтервали монотонності : на й функція зростає, а на й – спадає.

Зауваження 4. У точці максимуму розглянута функція має нульову похідну й дотична до графіка функції – горизонтальна. Про такий максимум говорять «гладкий максимум» (аналогічно «гладкий мінімум»). На противагу цьому, точка є точкою «негладкого мінімуму» – у цій точці похідна не існує, хоча є однобічні похідні. Відповідна точка графіка називається кутовою точкою графіка.

Приклад 2. Знайти екстремуми функції .

Розв‘язування. – існує скрізь.

– точка максимуму;

– точка мінімуму;

– точка мінімуму.

Лекція 13