§4. Дослідження функції на опуклість і перегин

I Напрямок опуклості (увігнутості)

Нехай функція диференційована на інтервалі . Диференційованість означає існування скінченої похідної, що, у свою чергу, означає наявність у графіка функції невертикальної дотичної. А для такої прямої є поняття «вище» і «нижче».

Означення 1. Диференційована функція називається опуклою вниз (вгору) на інтервалі , якщо її графік лежить не нижче (не вище) будь-якої

дотичної до графіка функції на .

Говорять ще: «графік функції спрямований опуклістю вниз (вгору)». Замість «опукла вниз (вгору)» говорять іноді «увігнута вгору (вниз)». Ще замість «опукла нагору» говорять просто «опукла», а замість «опукла вниз» – «увігнута».

На малюнку ліворуч зображений графік функції опуклої вниз, а праворуч – вгору.

Теорема 1 (перша достатня умова опуклості). Нехай функція має на інтервалі скінчену похідну другого порядку. Тоді:

1) якщо на , то спрямована опуклістю вниз;

2) якщо на , то спрямована опуклістю вгору.

Доведення. Позначимо: – ордината точки графіка функції з абсцисою ; – ордината точки дотичної до графіка з тією же абсцисою. Якщо – довільна точка з , то рівняння дотичної до графіка в точці з абсцисою має вигляд: . Складемо різницю ординат: . Існування означає, що існує (і неперервна) і, отже, – неперервна. Тоді до функції на проміжку застосовна теорема Лагранжа:

Тоді

Функція неперервна й диференційована, виходить, до неї можемо застосувати теорему Лагранжа на проміжку

Отже, для різниці ординат точки графіка й точки дотичної маємо рівність: . Можливі два випадки взаємного розташування точок :

В обох випадках добуток додатний, отже, : якщо , то , тобто графік розташовано вище дотичної, функція опукла вниз; якщо , те , графік розташовано нижче дотичної, функція опукла вгору. Теорема доведена.

Зауваження 1. Доведена теорема має просту геометричну ілюстрацію. Якщо функція опукла вниз, то кутовий коефіцієнт дотичної, тобто зростає, значить . Для опуклої вгору функції перша похідна спадає, виходить, друга похідна від'ємна.

Приклад 1. Дослідити на опуклість степеневу функцію

Маємо . Якщо або , те , а якщо , то . Виходить, на промені опукла вниз при й , і опукла вгору при . При або маємо лінійну функцію або . Такі функції можуть вважатися як опуклими вгору, так і опуклими вниз.

II Точки перегину

Означення 2. Точку називають точкою перегину графіка функції , якщо вона відокремлює ділянки графіка із протилежними напрямами опуклості.

Одна корисна властивість точки перегину: якщо в точці перегину існує дотична до графіка функції, то вона перетинає графік.

Зауваження 2. Часто цю властивість приймають за означення точки перегину. Але таке означення зовсім не рівносильне даному вище. Крива може й не мати дотичної у точці перегину, а може трапитися зворотне: крива перетинає дотичну в точці, що не відокремлює ділянки із протилежними напрямами опуклості. Прикладами можуть слугувати функції й : у першої в точках перегину й немає дотичних (хоча є однобічні дотичні), для графіка другої прямі і є дотичними.

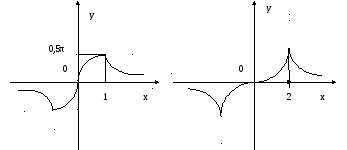
Можна навести й більш цікавий приклад:

Графік цієї функції на початку координат дотикається осі й перетинає її; тут існує неперервна друга похідна, але вона нескінченну множину разів міняє знак в околі нуля. (Надаємо читачеві змогу самому провести всі необхідні обчислення для цих функцій).

Приведемо без доведення ряд теорем, у яких використовується поняття критичної точки другого порядку.

Означення 3. Точка називається критичною точкою другого порядку функції , якщо друга похідна функції в цій точці дорівнює нулю або не існує.

Теорема 2 (необхідна умова точки перегину). Якщо – точка перегину функції , то – критична точка другого порядку.

Теорема 3 (перша достатня умова точки перегину). Нехай – критична точка другого порядку неперервної функції й нехай існує таке, що в околах і друга похідна існує й має протилежні знаки. Тоді точка – точка перегину графіка функції .

Теорема 4. (друга достатня умова точки перегину). Якщо функція має в точці скінчену похідну третього порядку й задовольняє умовам , , то графік цієї функції має перегин у точці .

Приклад 2. Знайти інтервали опуклості й точки перегину функції .

Рішення. У попередньому параграфі ми вже досліджували цю функцію на екстремум і одержали

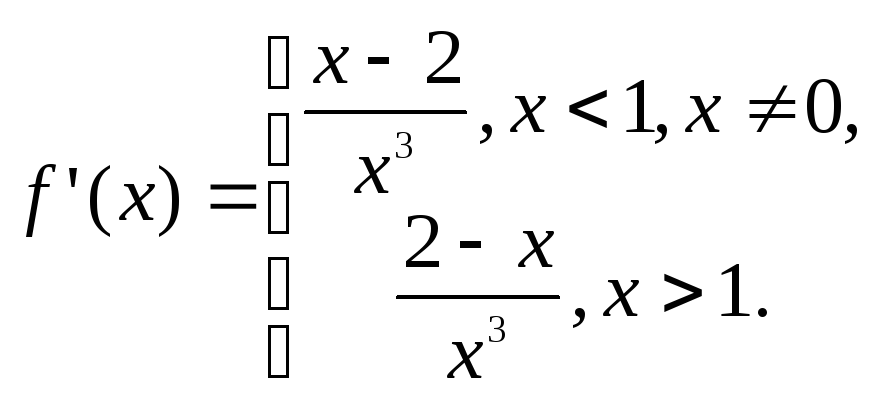
Знаходимо другу похідну:

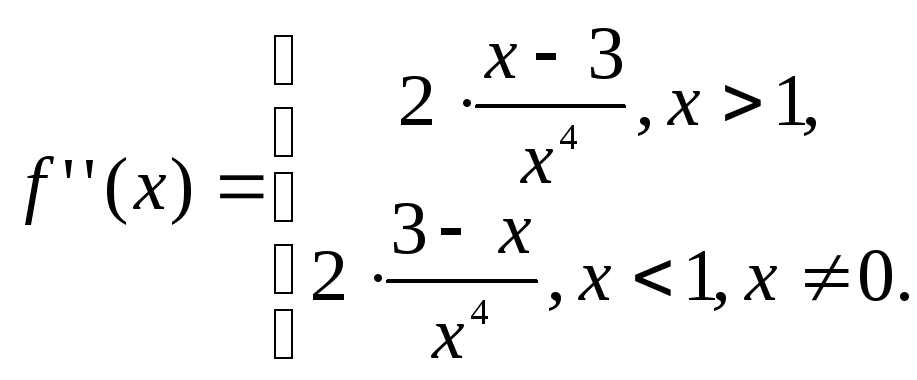
Нагадаємо, що не існує в точці , виходить, і не існує в цій точці, тобто ця точка – критична точка другого порядку. Ще одну таку точку знайдемо, розв‘язавши рівняння Ці критичні точки розбивають область визначення на інтервали знакопостійності другої похідної, тобто інтервали опуклості самої функції. Знаки визначаємо так само, як і знаки при дослідженні на екстремум. Приходимо до креслення:

Отже, маємо: на інтервалах , і функція опукла вниз, а на – опукла вгору; точки й – точки перегину.

ійй

Зауваження 3. У випадку недиференційованої функції прийняте інше означення опуклості, а саме: функція називається опуклою вниз (вгору) на інтервалі , якщо всі точки будь-якої дуги її графіка лежать під (над) відповідною хордою або на ній. Для диференційованої функції це означення рівносильне даному вище.

Зауваження 4. Третя достатня умова перегину буде дана в наступній темі.