§4. Розкладання по формулі Маклорена деяких елементарних функцій

I. .

Оскільки й , то формула Маклорена має вигляд

^{де: 1)}

²⁾ , для будь-якого проміжку (очевидно, що ).

II. .

^{Відомо, що Тоді:}

Умови теореми з §3 виконані на всій осі з Формула Маклорена має вигляд

^{де: 1)}

2) .

На перший погляд написані форми для відрізняються від загальних результатів. Але треба не забувати, що, загалом кажучи, у розкладанні для можна дописати ще один член з , тільки коефіцієнт при цієй степені дорівнює нулю.

III. .

Аналогічно попередньому неважко одержати

де: 1)

^{2) .}

IV. .

Насамперед, маємо . Тепер можна використати формулу дифе-ренціювання степеневої функції:

При Формула Маклорена має вигляд (з урахуванням того, що ):

де: 1)

2)

Відзначимо, що для оцінки залишкового члена для потрібна форма , відмінна від форми Пеано й Лагранжа. Крім того, користуватися розкладанням у наближених обчисленнях можна тільки для : ^{тільки для таких значень} .

V. .

Оскільки

то

Формула Маклорена для цієї функції має вигляд:

Тут для залишкового члена маємо: Як і у випадку логарифмічної функції для оцінки потрібна форма, відмінна від Пеано й Лагранжа. Більш докладно про це ми будемо говорити в третьому семестрі в темі «Степеневі ряди». Відзначимо тільки, що написаним розкладанням у наближених обчисленнях можна користуватися лише для

VI. Інші функції. Користуючись відомими розкладаннями, можна, не обчислюючи похідних, безпосередньо писати розкладання із залишковим членом у формі Пеано й для більш складних функцій. При цьому всі степені х, до призначеної включно, враховуємо точно, а більш високі степені будемо відразу включати в (не виписуючи їх).

Приклад 1. Написати розкладання функції до .

З пункту I маємо:

де залишковий член

, тому що . Далі, пункт II дає: . У такий спосіб

Після спрощення одержимо шукане розкладання

Приклад 2. Написати розкладання функції до члена с.

Згідно IV,

.

Необхідне розкладання для (див. III) випишемо в декількох варіантах:

.

З огляду на, крім усього, і ~ –0,5х², х→ 0, одержимо:

Після приведення подібних членів будемо мати:

.

§5. Застосування формули Маклорена

I Обчислення границь

В §11 теми «Введення в математичний аналіз» були наведені т.зв. асимптотичні формули (ще говорять «асимптотичні оцінки») такі, як: (при ) і т.п. Фактично вони є окремими випадками формул Маклорена для відповідних функцій. Для обчислення простих границь тих формул було досить. Однак, при роботі зі складними границями потрібні формули Маклорена більш високого порядку. Наприклад, границя

за допомогою формули обчислити неможливо, тому що

Якщо ж візьмемо для формулу Маклорена третього порядку , легко одержимо

Розглянемо більш складні приклади.

Приклад 1. Обчислити границю

Для обчислення використовуємо такі формули:

, де

Маємо:

.

Приклад 2. Часто студенти вважають, що при

.

Доведемо за означенням, що це не так. Дійсно,

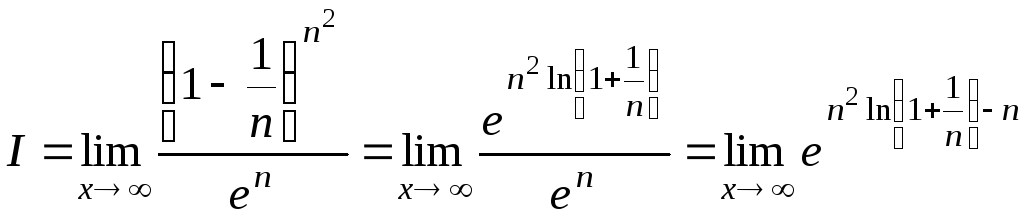
Обчислимо окремо межу показника степеня, використовуючи формулу Мак-лорена із при:

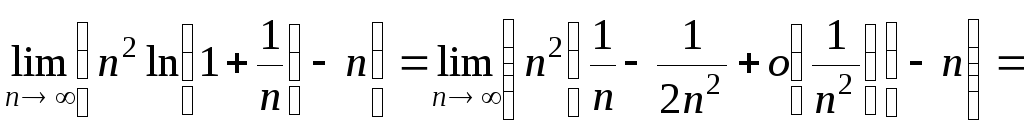
Використовуючи неперервність показникової функції, можемо записати: . Отримана границя відмінна від 1, це й означає, що передбачувана еквівалентність невірна.