69

Тема похідна

Лекція 8

§1. Задачі, що приводять до поняття похідної

I Задача про дотичну

Означення. Дотичною до лінії L у її точці М₀ називається граничне положення січної M₀M, коли точка M уздовж лінії L прагне довільним образом до збігу із точкою M₀.

Щоб додати математичну строгість цьому визначенню, будемо вважати, що лінія L – це графік деякої функції .

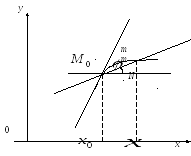Нехай – фіксована точка графіка, а –поточна точпка. Позначимо . Прагнення точки M до М₀ рівносильне або . Через точку М₀ проходить багато прямих, всі вони відрізняються одна від одної кутовими коефіцієнтами. Дотична до графіка в точці М₀ – це та пряма, кутовий коефіцієнт якої є границя кутового коефіцієнта січної M₀M при :

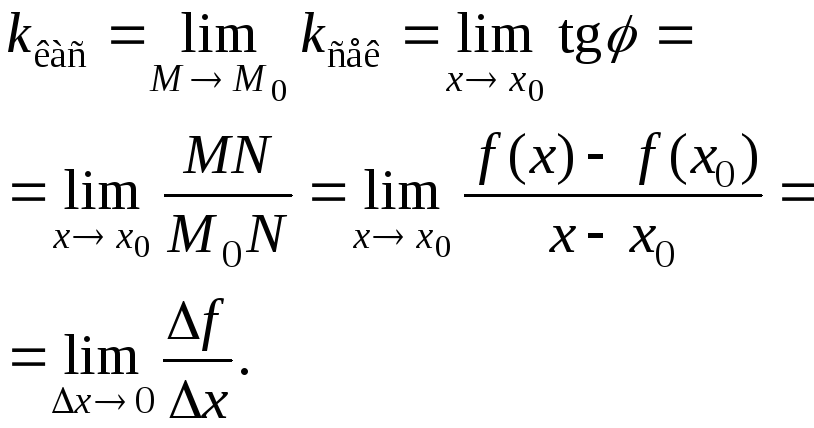
II Задача про швидкість

Нехай по прямій, на якій обрано початок відліку, одиниця виміру й напрямок, рухається точка за законом ( – це координата точки на прямій у момент часу t ). Важливою характеристикою руху є швидкість. Для рівномірного руху (тобто руху з постійною швидкістю) можна взяти довільний проміжок часу й розділити пройдений шлях на тривалість проміжку часу, тобто на . Саме тому, що швидкість постійна, отримана відповідь не буде залежати ні від , ні від .

У загальному випадку руху зі змінною швидкістю відношення є не що інше як середня швидкість руху за проміжок . Середня швидкість тим краще характеризує рух, чим менше тривалість . Спрямовуючи до нуля, ми й отримаємо миттєву швидкість .

Зауваження. Дві різні задачі, розглянуті вище, привели в процесі розв‘язування до однакового результату – границі відношення приросту функції до приросту аргументу за умови, що останнє прагне до нуля. Є багато задач у самій математиці й у її застосуваннях, які приводять до необхідності обчислення таких границь.

§2. Означення й зміст похідної

Розглянемо функцію , визначену в точці й у деякому її околі. Надамо аргументу x приріст , що не виводить аргумент за межі околиці. Функція одержить приріст .

Визначення. Границя відношення приросту функції до приросту аргументу при (якщо ця границя існує і скінчена) позначається й називається похідної функції по змінній x у точці x₀.

Таким чином,

.

З означення випливає, що похідна – це число. Однак найчастіше виявляється, що це число можна обчислити не тільки в одній точці x₀, а у всіх точках деякого інтервалу. Тим самим на цьому інтервалі визначається деяка нова функція, що теж називається похідної функції й позначається: . Крім цих позначень використовуються й інші:

– похідна як функція (читається “де ігрек по де ікс”),

– похідна у фіксованій точці x₀.

Порівнюючи результати, отримані в §1, з означенням похідної, можна надати похідній зміст:

1) якщо – закон руху, то ;

2) – це кутовий коефіцієнт (тангенс кута нахилу до осі Ox) дотичної до графіка функції в точці з абсцисою x₀.

Використовуючи 2) легко написати рівняння дотичної:

і нормалі, тобто прямої, що проходить через точку дотику перпендикулярно дотичній:

.

Приклад. Обчислити (за означенням) похідну функції .

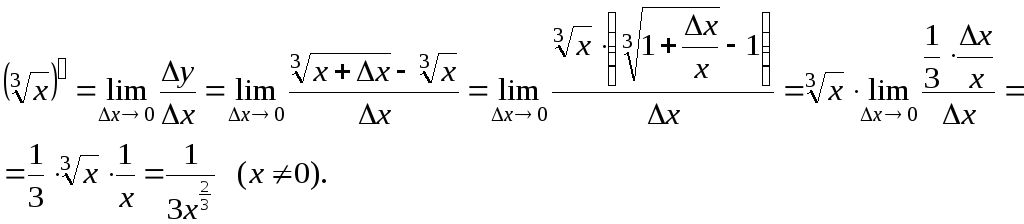
Зауваження 1. Похідну зручно розуміти як швидкість зміни функції щодо аргументу x.

Зауваження 2. Відношення приросту функції до приросту аргументу називають різницевим відношенням функції.