IV Тригонометричні функції

1. y=sinx

.

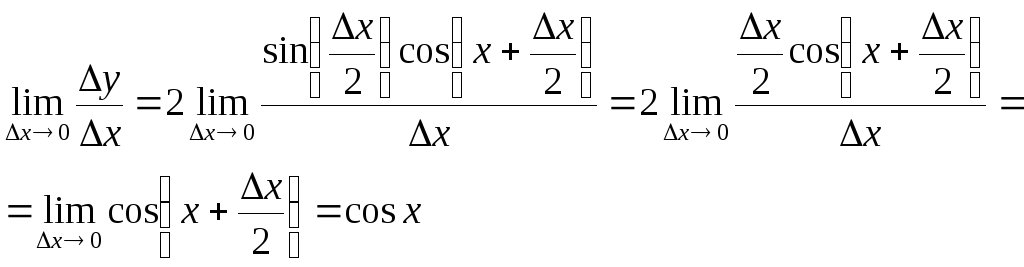
(на останньому кроці ми скористалися неперервністю косинуса).

Отже,

.

Похідні інших тригонометричних функцій можна обчислити, використовуючи означення похідної, але простіше використовувати відомі правила диференціювання й формули, що зв'язують тригонометричні функції один з одним.

2. y=cosx

.

Отже,

.

3. y=tgx

.

Отже,

.

4. y=сtgx.

Аналогічно попередньому можна одержати

(ctg.

V Обернені тригонометричні функції

Похідні цих функцій найпростіше одержати за допомогою основної тотожності, що зв'язує пари взаємно обернених функцій, а саме: .

1. y=arcsinx

Диференціюємо почленно тотожність :

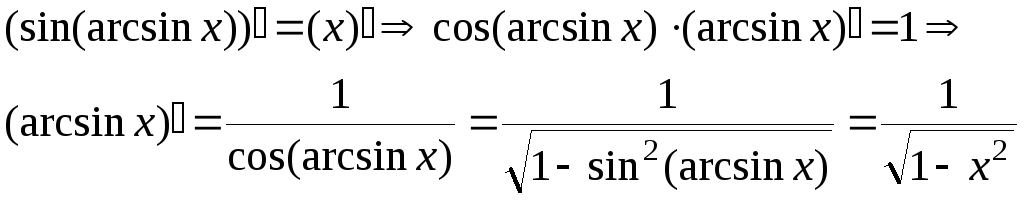
(нагадаємо, що , тому).

Отже,

.

2. y=arccosx

Відоме співвідношення й попередня формула для, дозволяютьотримати

.

3. y=arctgx

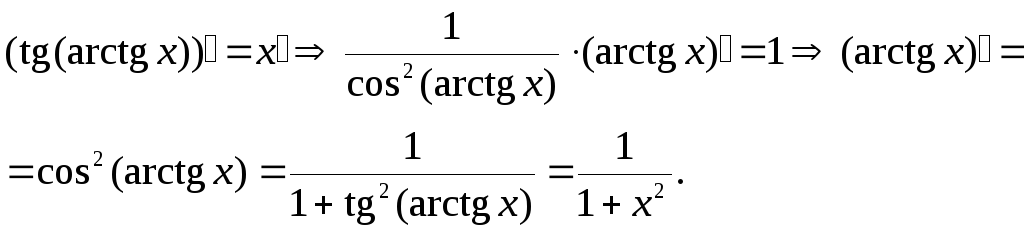
Отже,

.

4. y=arcctgx

Зі співвідношення ,будемо мати

.

Зауваження 3. Покажемо на прикладі як можнаодержувати похідні аркфункцій, виходячи з означення похідної. Приріст арктангенса прагне до 0 при(через неперервність функції). Звідсиодержуємо еквівалентність: при Тепер можна легко знайти границю різницевоговідношення:

.

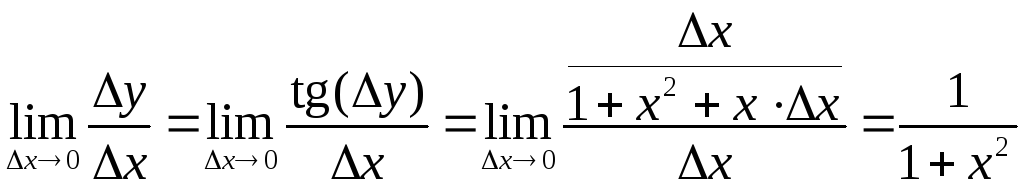Зауваження 4. Похідні аркфункцій можна одержати також, використовуючи загальне правило диференціювання оберненої функції, що буде наведено нижче.

VI Гіперболічні й обернені гіперболічні функції

Ці функції елементарним образом виражаються через показникову й логарифмічну функції. Тому найпростіше знаходити їхні похідні, використовуючи відомі правила диференціювання.

Наприклад:

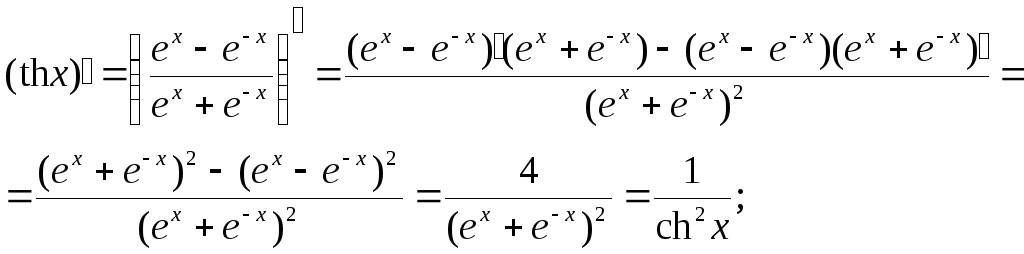
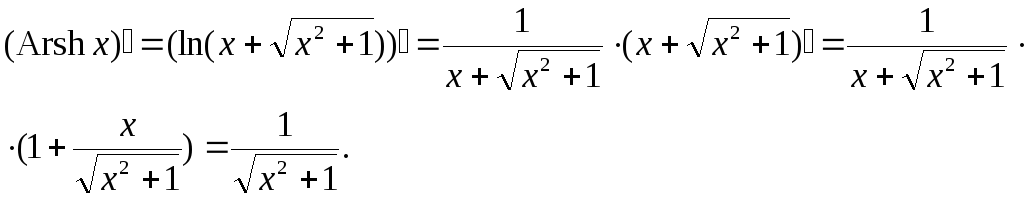
Похідні інших функцій цієї групи студентам пропонується одержати самостійно.

VII Зведення формул для похідних

1. ,,,.

2. ,.

3. ,.

4. . 5..

6. (tg. 7. (ctg.

8. . 9..

10. . 11..

12. . 13..

14. . 15..

16. .

17. .

18. .

§5 (Продовження). Основні правила диференціювання

VII Логарифмічна похідна

Нехай функція додатна йдиференційована. Тоді й функція –диференційована, причому

.

Цей вираз й називається логарифмічною похідною функції . Звідси легкоодержати похідну самої функції :

.

Використовуючи цю формулу, можна отримати правило диференціювання складної степенево-показникової функції:

.

Остаточно маємо формулу:

.

Зауваження 2. Загалом кажучи, завжди краще пам'ятати не зайву формулу, а прийом, що приводить до цієї формули. Для степенево-показникової функції можна запропонувати прийом, що використовує основну логарифмічну тотожність:

.

П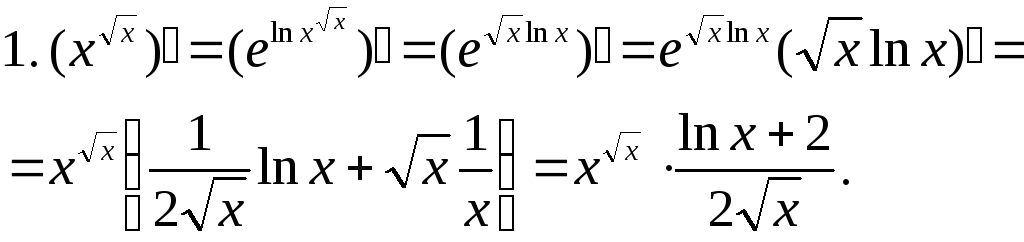риклади.

2.

VIII Диференціювання оберненої функції

Нехай функція в деякомуоколі точки – неперервна й строго монотонна, а крім того,диференційована в точці , причому. Тоді в деякомуоколі точки існує обернена функція, також неперервна, строго монотонна йдиференційована в точці , причому

. (1)

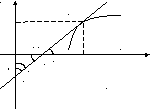
Строге доведення наводити не будемо, але дамо геометричну ілюстрацію. При цьому використовуємо той факт, що графіки взаємо-обернених функцій ізбігаються, а похідна – це кутовий коефіцієнтдотичної.

,

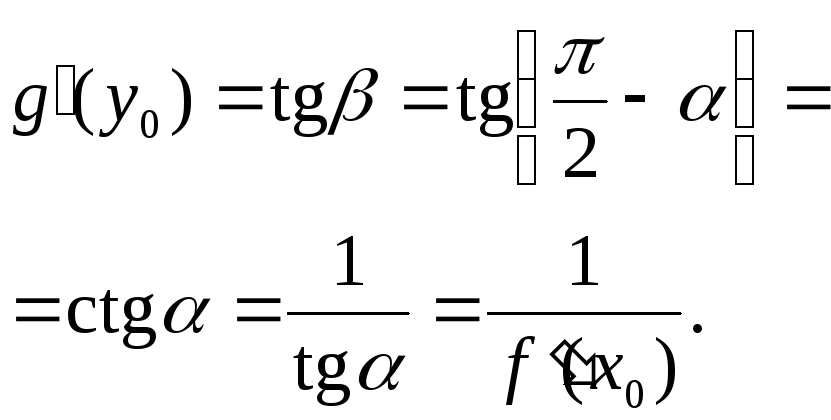
Формулу (1) записують ще у вигляді або.

Застосуємо останню формулу для обчислення похідної, наприклад, арксинуса:

,

IX Диференціювання функції, даної в параметричній формі

Нехай є система параметричних рівнянь ,, причому функціїйдиференційовані й зберігає знак. Тоді наобласті значень функції існуєдиференційована функція , причому

Дійсно, з умови (або) випливає монотонність функції; отже, у неї існує обернена. Тоді– деяка функція відx. Її похідну можна знайти, якщо застосувати правила диференціювання складної й оберненої функцій:

Приклад. 3. Складемо рівняння дотичної до еліпса вточці , що відповідає значенню параметра.

Координати точки дотику: ,.Куто-вий коефіцієнт дотичної

.

Шукане рівняння має вигляд: .

Зауваження 3. Загалом кажучи, похідна функції, даної параметрично, є функція, заданая параметрично. Методично більш правильним було б писати таку похідну у вигляді системи параметричних рівнянь: