§3. Нескінченні й однобічні похідні

I Нескінченні похідні

Означення 1. Говорять, що функція має в точці x₀ нескінченну похідну, якщо

.

При цьому пишуть або .

Приклад 1. , :

.

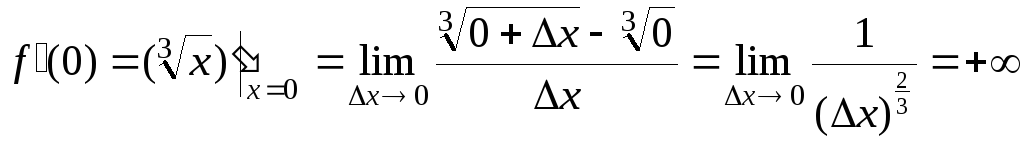II Однобічні похідні

Визначення 2. Права й ліва похідні функції в точці x₀, визначаються рівностями:

и .

Із загальних теорем про границі можна одержати таку теорему.

Теорема 1. Функція має в точці x₀ похідну тоді й тільки тоді, коли вона має в цій точці рівні одна одній однобічні похідні.

Приклад 2. Для функції знайти праву й ліву похідну в нулі.

,

.

Тому що , то не існує.

Наступна теорема дозволяє в деяких випадках спростити обчислення однобічних похідних.

Теорема 2. Нехай функція має в інтервалі скінчену похідну , причому, існує (скінчений чи ні) . Тоді в точці x₀ існує права похідна й .

Аналогічне твердження має місце й для лівої похідної.

В §2 була обчислена похідна функції для : 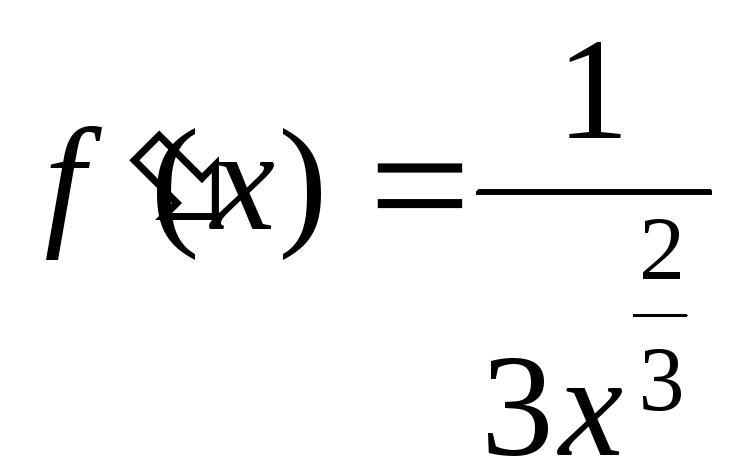. Результат приклада 1 ( ) за допомогою теореми 2 виходить моментально:

.

Аналогічно виходить і . Збіг однобічних похідних означає, що й .

Зауваження. Якщо у функції існують скінчені, не рівні одна одній похідні й , то у графіка функції є не співпадаючі права й ліва дотичні в точці . Така точка графіка називається кутовою. Якщо ж похідна (хоча б однобічна) дорівнює + або , то це означає, що у графіка є вертикальна дотична.

§4. Диференційовності функції

Означення. Говорять, що функція диференційовна в точці x₀, якщо її приріст можна представити у вигляді

(1)

де A – деяке число, що не залежить від .

Теорема 1. Для того, щоб функція , була диференційовна у точці x₀, необхідно й достатньо, щоб вона мала в цій точці скінчену похідну.

Доведення. Необхідність. Нехай диференційовна. Розділимо обидві частини рівності (1) на :

.

Переходячи до границі при , отримаємо

,

тобто у точці x₀ існує похідна й вона дорівнює A: .

Достатність. Нехай існує скінчена похідна . Тоді

й, отже, .

У цьому співвідношенні неважко побачити рівність (1). Теорема доведена.

Таким чином, для функції однієї змінної диференційованість і існування скінченої похідної – поняття рівносильні.

Формулу

називають формулою нескінченно малих приростів.

Між поняттями диференційованості й неперервності існує зв'язок, який дається наступною теоремою.

Теорема 2. Якщо функція диференційовна в точці x₀, то вона й неперервна в цій точці.

Дійсно, з формули (1) витікає, що , а це і є одне з означень неперервності.

Природно виникає питання про те, чи справедливо твердження, зворотне теоремі 2, тобто “неперервна функція диференційовна ”. На це питання варто дати негативну відповідь: існують функції, неперервні в деякій точці, але не диференційовні в даній точці. Прикладом може служити функція із приклада 2 §3: . Вона неперервна в нулі, але не існує.

Наведемо ще один приклад такої функції.

Приклад 1.

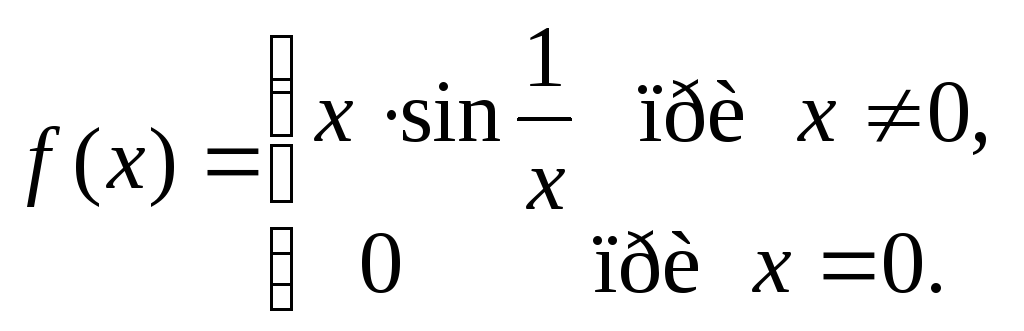
Дана функція – неелементарна, можлива точка розриву (у цій точці один елементарний вираз міняється на інший). Але

,

отже, неперервна в точці . Знайдемо похідну функції в нулі (за означенням!):

.

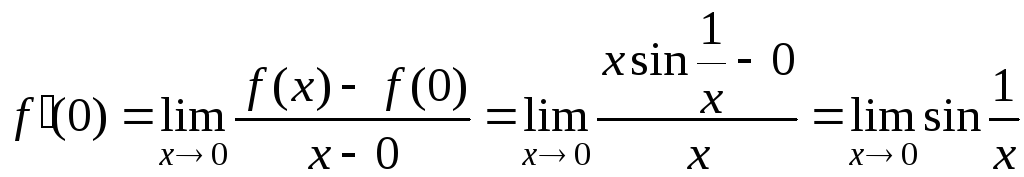Але нам уже відомо, що, коли аргумент синуса прагне в , синус границі не має. Отже, не існує, тобто не є диференційовна в нулі.

Зауважимо, що математиками побудовані приклади функцій, неперервних на деякому проміжку, але які не мають похідної в жодній точці цього проміжку.

Лекція 9