III Таблиця еквівалентностей

При :

1) ; 2); 3);

3) ; 5); 6);

7) ; 8); 9);

10) ; 11); 12);

13) .

Крім цих формул використовуються ще такі:

14) многочлен на еквівалентний старшому члену, а в нулі  молодшому;

15) при, якщо тілький;

16) ,при(,);

17) при.

Частина цих формул була отримана в §10. Виведемо ще кілька інших:

5) ;

10) ;

13) ;

15) Нехай , Тоді, тобто(у широкомузмісті).

IV Використання еквівалентностей для обчислення границь

Теорема. Нехай , апри. Якщо, то й.

Доведення.

.

Практичний висновок. При обчисленні границь часток і добутків функцій кожну з них можна замінити еквівалентною.

Приклади.

4.

.

Тут були використані еквівалентності для синуса, логарифма, арктангенса, степеневої функції й виразу типу многочлена (алгебраїчної суми степенів змінної з невід‘ємними показниками, а не тільки натуральними, як у звичайному многочлені).

5. Обчислимо границю . Використовуючиосновну логарифмічну тотожність, властивість логарифма степені й неперервність функції ,одержимо:

.

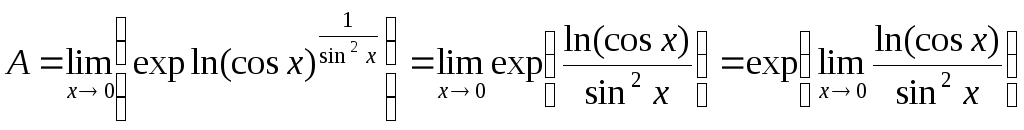Виведемо потрібну тут формулу еквівалентності при :

.

Отже, .

6. Приведемо ряд прикладів «підгонки» під табличну форму

еквівалентності:

при ;

при ;

при .

Зауваження-застереження. Використовувати еквівалентності (у зазначеній формі ) у сумах, різницях функцій і під знаками функцій, загалом кажучи, не можна.Виключення становить степенева функція, тобто, якщо , то,.

Однак, існує інша форма еквівалентностей, яку можна використовувати скрізь. Цю форму розглянемо в наступній частині параграфа.

V Асимптотичні формули

В наслідок другого означення еквівалентності співвідношення рівносильнеабо. Таким чином, таблицю еквівалентностей можна записати у формі т.зв.асимптотичних формул. Приведемо лише деякі з них. Всі інші формули студенти повинні вміти виводити самостійно.

Отже, при :

, ,

, ,

, .

Ці асимптотичні формули можна застосовувати в сумах, різницях і під знаками функцій. Однак, не завжди вони дають відповідь на поставлене питання.

Приклади.

7.

.

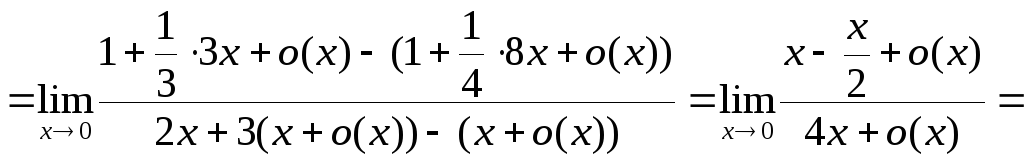
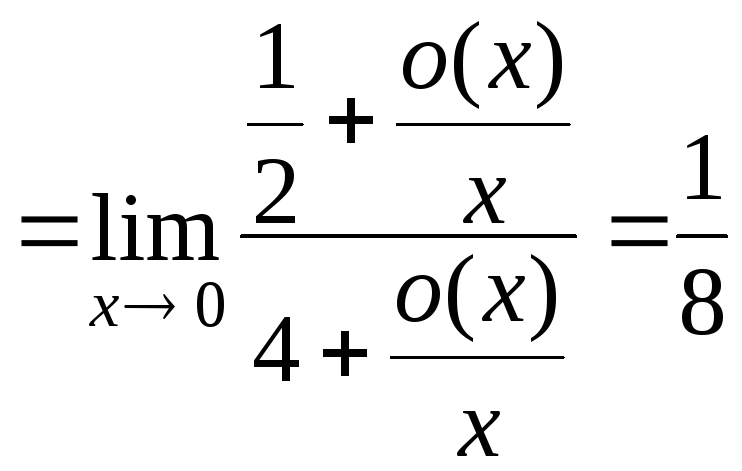Тут використаний той факт, що за означенням символу маємо:.

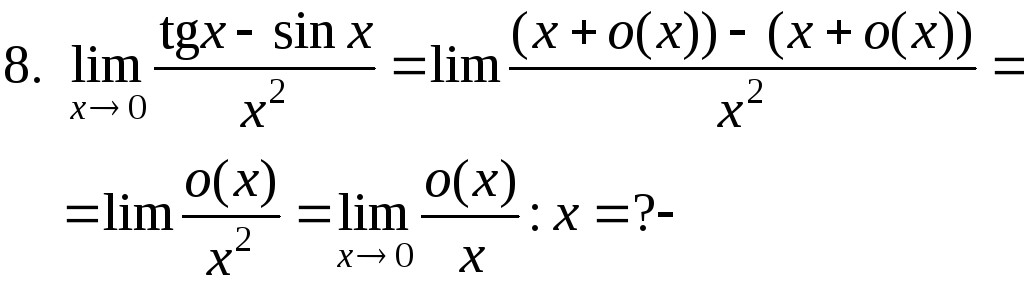
частка нескінченно малих може бути якою завгодно. Така ситуація означає, що відповідна асимптотична формула недостатньо точна. У темі «Формули Тейлора й Маклорена» будуть дані уточнення:

, .

Задача. Обчислити границі:

а) ; б).

Лекція 7

§12. Поняття неперервності функції

Розглянемо функцію y=f(x), визначену в точці x₀ і в деякому її околі.

Означення 1. Функція f(x) називається неперервної в точці x₀, якщо

. (1)

Тому що , то співвідношення (1) можна записати в такомувиді:

,

тобто, для неперервної функції можна знак границі вносити під знак функції.

Дамо ще одне означення неперервності, що рівносильне означенню 1. Для цього в рівності (1) перенесемо f(x₀) у ліву частину й внесемо під знак границі. Умови x x₀ і (x – x₀)0 рівносильні, тому одержуємо:

(2)

Різниця x – x₀ називається приростом аргументу x у точці x₀ і позначається Δx, а різниця f(x)– f(x₀) – приростом функції й позначається Δy. У цих позначеннях рівність (2) приймає вид:

. (3)

Це співвідношення і є ще одне означення неперервності, яке можна сформулювати так:

Означення 2. Функція f(x) називається неперервної в точці x₀, якщо її приріст Δy=o(1) при Δx0.

Приклад. Доведемо неперервність y=sinx у довільній точці x₀ .

Отриманий вираз є добуток обмеженої функції на нескінченно малу (з леми 2 §10 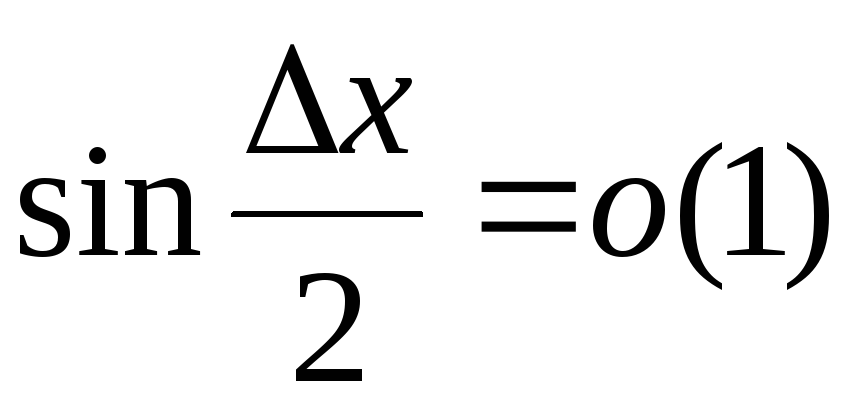при Δx0 ). По однієй із властивостей н.м. функцій одержуємо Δy=o(1) при Δx0, що й доводить неперервність y=sinx у довільній точці x₀ .

Означення 3. Функція f(x) називається неперервною в точці x₀ ліворуч (праворуч), якщо

.

Наприклад, функція y=[x] неперервна праворуч у будь-якій цілій точці, тому що [k+0]=[k]=k, у той же час ліворуч вона не є неперервної через те,що [k–0]=k–1≠[k].

Із відомих теорем про границі функцій легко одержати такі результати.

Теорема 1. Функція f(x) неперервна в точці x₀ тоді й тільки тоді, коли вона неперервна в цій точці, як праворуч, так і ліворуч, тобто

f(x₀+0)= f(x₀ – 0)= f(x₀).

Теорема 2. Нехай функції f(x) і g(x) неперервні в точці x₀, а функція F(u) неперервна в точці u₀=f(x₀). Тоді й функції f(x)±g(x), f(x)·g(x), f(x): g(x) (за умови g(x₀)≠0 ) и F(f(x)) неперервні в точці x₀.

Якби ми могли довести неперервність всіх основних елементарних функцій (як ми це зробили для синуса), то з теореми 2 ми одержали б ще один важливий результат.

Теорема 3. Усяка елементарна функція неперервна в будь-якій точці її області визначення ( що входить у цю область із деяким околом).

Означення 4. Говорять, що функція f(x) неперервна на проміжку , якщо вона неперервна в будь-якійточці проміжку (у граничних точках проміжку мається на увазі одностороння неперервність).