§8. Монотонні послідовності. Число

I Про границю монотонної послідовності

Уже відомо, що збіжна послідовність – обмежена. Однак, не всяка обмежена послідовність має скінчену границю: прикладом може слугувати послідовність .

Однією з умов, що забезпечують існування границі, є монотонність обмеженої послідовності.

Теорема. 1. Усяка обмежена монотонна послідовність має скінчену границю. 2. Усяка необмежена монотонна послідовність є нескінченно великою (певного знака).

Помітимо, що для спадної послідовності досить доводити обмеженість знизу, а для зростаючої – обмеженість зверху.

Приклад. Розглянемо послідовність із загальним членом . Для доведення монотонності перетворимо член:

.

Ми отримали рекуренте співвідношення , де.

Члени даної послідовності додатні, а , отже,, тобто спадає. Її обмеженість знизу очевидна, тому що .

Сформульована вище теорема забезпечує існування скінченної границі . Для послідовностілегкоотримати:

, тобто .

Тепер перейдемо до границі в обох частинах рекурентного співвідношення, причому в правій частині маємо право використовувати теорему про границю добутку (тому що й збіжні):

або .

Звідси одержуємо: .

II Число е

Розглянемо послідовність із загальним членом і спробуємозастосувати до неї теорему, сформульовану вище.

Монотонний характер безпосередньо не вбачається, тому щозі зростанням показника степені основа степені спадає. Щоб переконатися в монотонності, розкладемо степінь по формулі бінома Ньютона:

Якщо тепер від перейти до, тобто збільшитина одиницю, то, по-перше, додасться ще один (додатний) доданок, а, по-друге, кожен із уже написаних доданків збільшиться, тому що множники виду замінятьсябільшими множниками . Звідси маємо, що,

тобто послідовність  зростаюча.

В останньому виразі для замінемо всідужки на 1. Тим самим кожний доданок збільшиться й ми одержимо оцінку:

.

З огляду на те, що , підсилимо цю оцінку:

.

(Тут використана формула для суми геометричної прогресії). Отже, послідовність зростає й обмежена зверху, отже, вона має скінчену границю. Її позначаютьбуквою . Це число

має виняткову важливість, як для самого математичного аналізу, так і для його застосування.

Лекція 5

§9. Границя функції

I Загальне означення

Домовимося про термінологію. Термін «число » означає як звичайне число, так іодин із символів: або. Термін «точка » означає як скінчену точку, так і «нескінченновіддалену»: ,або. При цьому під околом такої «нескінченновіддаленої» точки розуміється інтервал або об'єднання цих інтервалів відповідно (придовільному ).

Околом же скінченої точки розуміємо будь-який інтервал, що містить цю точку. Для простоти формулювань і для нескінченно великих послідовностей будемо казати: «послідовність сбігається (до або)».

Розглянемо функцію ,визначену в деякому околі точки (за винятком, мабуть, самоїточки ) і візьмемо із цього околу послідовністьточок

відмінних від і збіжну к. Значення функції вточках цієї послідовності також утворять числову послідовність

і можна порушувати питання про існування її границі.

Означення 1 (мова послідовностей). Число називають границею функціївточці (або при) і пишуть

(або: при),

якщо для будь-якої збіжної до послідовності (1) значень аргументу,відмінних від , відповідна послідовність (2) значень функції збігається до числа.

Геометричний зміст рівності :графік функції в околі точки наближається доточки .

Приклад 1. Обчислимо границю функції вточці .Розглянемо довільну послідовність і. Для відповідної послідовності значень функціїмаємо. Таким чином,.

Приклад 2. Покажемо, що границя функції прине існує.Розглянемо дві послідовності значень аргументу зі членами й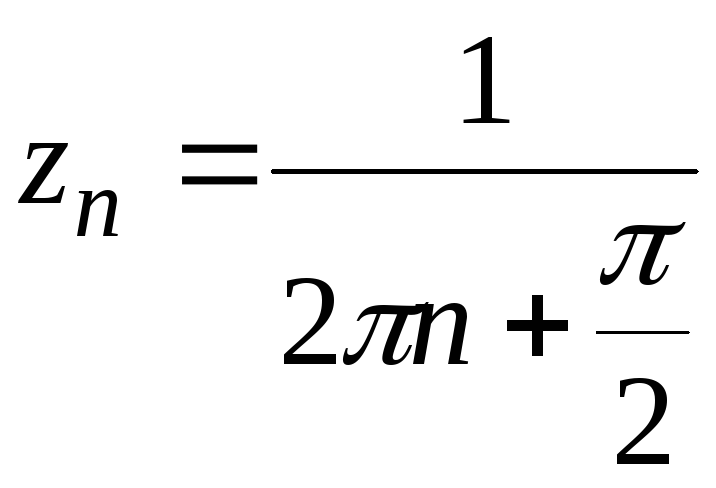. Очевидно, що. При цьому для послідовностей значень функції:

,

.

Таким чином, для двох збіжних до 0 послідовностей значень аргументу відповідні послідовності значень функцій мають різні границі. А це за означенням границі функції й означає, що не існує.