42

Розділ диференціальне числення Тема введення в математичний аналіз

Лекція 1

§1. Функції однієї змінної: основні поняття

I Означення

Розглянемо дві змінні величини x і y. Якщо за деяким правилом або законом кожному значенню змінної величини x поставлено у відповідність одне певне значення змінної величини y, то говорять, що y є функція від x і пишуть: y=f(x) або y=y(x).

Використовувана термінологія: x – незалежна змінна, y – залежна змінна; x – аргумент, y – функція.

У позначенні y=f(x) буква f є характеристикою функції й символізує правило, про яке говориться у визначенні. Якщо розглядаються різні функції, то їхні характеристики позначаються різними буквами. І взагалі, будь-який запис виду u=g(v) означає, що змінна u є деяка функція змінної v.

II Способи завдання функції

Задати функцію означає задати правило (закон) відповідності. Найбільш уживаним є завдання цього правила за допомогою однієї або декількох формул, що містять вказівку на ті операції або дії над постійними числами й над значеннями аргументу x, які необхідно зробити, щоб одержати відповідне значення функції y. При цьому розрізняють три варіанти цього т.зв. аналітичного способу завдання:

1. явний, наприклад, 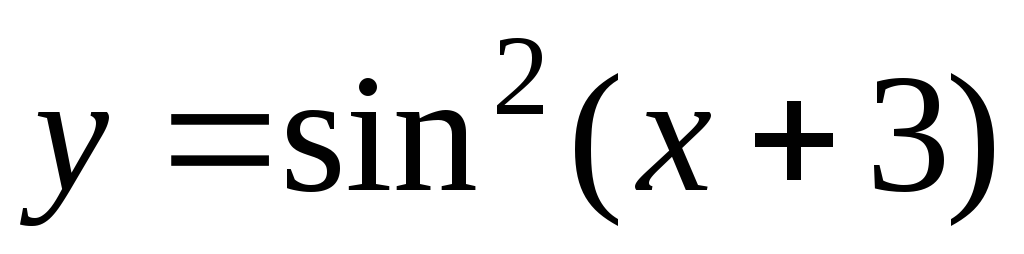або

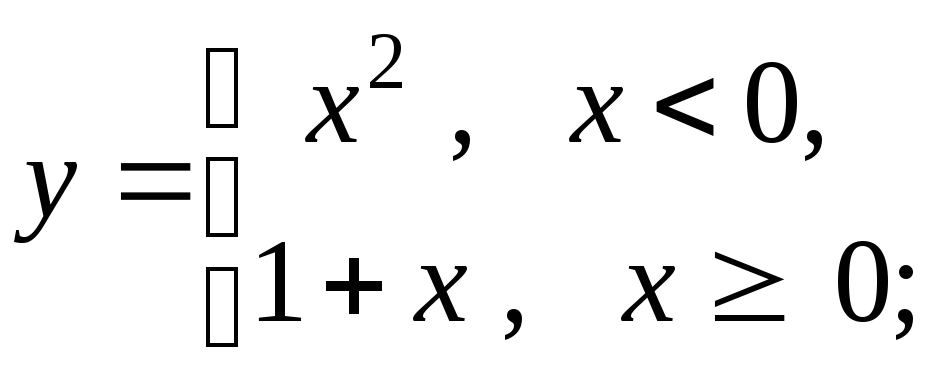
2. неявний, наприклад, 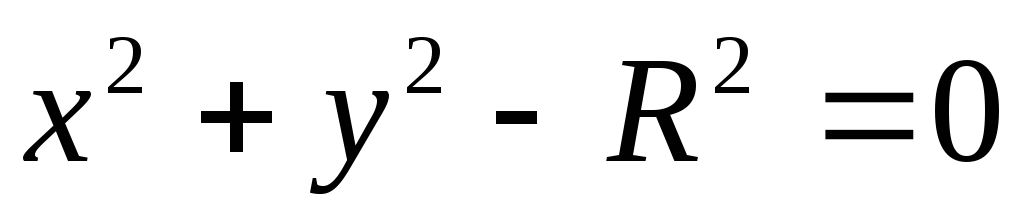(змінні x і y зв'язані деяким рівнянням виду F(x, y)=0);

3. параметричний, наприклад, 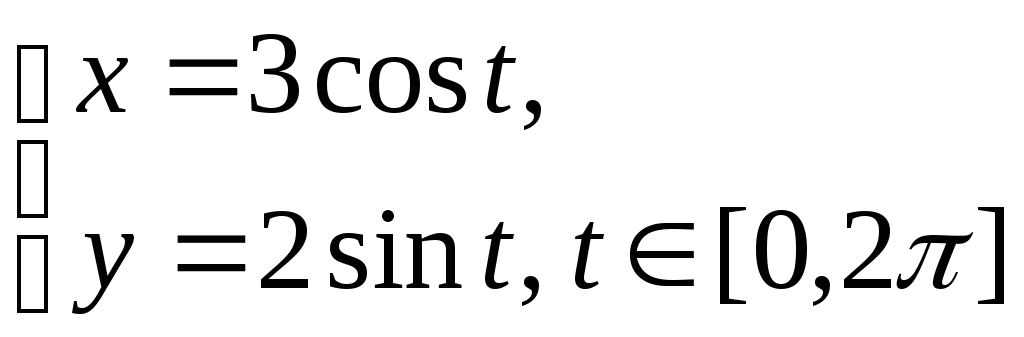(змінні x і y задані як явні функції допоміжної змінної – параметра t).

На практиці часто використовують табличний спосіб завдання функції, коли задаються таблиця окремих значень аргументу й відповідних їм значень функції. Існують методи що дозволяють обчислити (приблизно!) значення функції, що відповідають проміжним значенням аргументу, а також підібрати формулу, що задає функцію з певною точністю.

Досить розповсюдженим, особливо в експериментальних науках, є графічний спосіб завдання функції, при якому відповідність між аргументом і функцією задається за допомогою деякої лінії в системі координат xOy.

Використовують у математиці й словесний спосіб завдання, коли функція описується правилом її складання. Така, наприклад, функція y=[x]: “ є ціла частина x”, тобто найбільше ціле, що не перевершує числа x. Поряд із цілою частиною, розглядають і функцію дробова частина числа: {x}=x[x]. Приклади: [2,8]=2, [–3,4]= – 4, [2]=2.

III Область визначення й область значення функції

Множина D(y) тих значень аргументу x, для якого визначені відповідні значення функції y=f(x), називають областю визначення функції. При знаходженні області визначення функції, заданої аналітично, необхідно мати на увазі наступне:

1) якщо , то ;

2) якщо , то ;

3) якщо , то ;

4) якщо , .

Множина E(y) тих значень залежної змінної , які вона приймає, коли залежна змінна пробігає D(y), називають областю значень функції.

Для основних елементарних функцій (див. нижче) області значень відомі. У загальному ж випадку для знаходження E(y) потрібне дослідження функції за допомогою похідних.