Задача про зустріч

Визначити кількістьтаких перестановок чисел, щоточно елементівіз знаходятьсяна своїх місцях(тобто), а інші, перебуваютьу безладі.

Інакше: нас цікавлятьперестановки, в яких рівно елементів нерухомі.

Розв’язання.

Із загальногочисла елементів вибирається , які залишаютьсяна своїх місцях. Оскільки вибір елементу визначає й його місце розташування, то кількість варіантів дорівнює: . Для інших елементів розв’язується задача про безлад: . Тоді,за правилом добутку кількість способів, якими можна переставити елементівпри таких умовах, дорівнює:

Перестановки без фіксованих пар

Позначимочерез число таких перестановок чисел, що жодна з цихперестановок не містить жодної з упорядкованих фіксованихпар:

Розв’язання.

Для обчислення використовуємопринцип включення і виключення.Позначимочерез властивістьперестановки містити-ту впорядкованупару.Для обчислення скористаємосядругимокремим випадкомдля формули включень-виключень. Число всіхперестановок.Перестановки, що володіють властивістю , виходятьяк перестановки елементів тапари , що розглядається.як один елемент. Отже, незалежно від маємо:

Для перестановок, що володіють двома властивостями, тобто мають дві впорядкованіпари, наприклад та, розглянемодва випадки:

1) , пари йдутьне поспіль;

2) , пари розташованіодна за одною.

1) Якщо, то пари йдутьне поспіль.

У цьому випадку маємоперестановки двохпар, як окремих, складних елементів:та і елемента,що лишилися. Тобто всього переставляються елемента.

2) Якщо , то перестановки складаємо з однієї впорядкованої трійки елементів: та інших елементів, тобто теж із елементів.

Таким чином, число перестановок, що володіють двома властивостями, так само:

Аналогічно, число перестановок, що володіють властивостями, залежить тільки від ідорівнює:

Тоді, загальнечисло перестановок без фіксованихпардорівнює:

Наприклад.

1. Скільки різних слів можна згенеруватиізбукв слова"тік-так", щоб ніякі однакові буквине йшлиодназа одною?

Розв’язання.

Вcього в слові"тік-так": 6 букв серед яких дві букви"к" і дві букви"т".

Нехай – дві букви "т" йдуть одна за одною;

–дві букви "к" ідуть одна за одною.

Тоді , маємо:

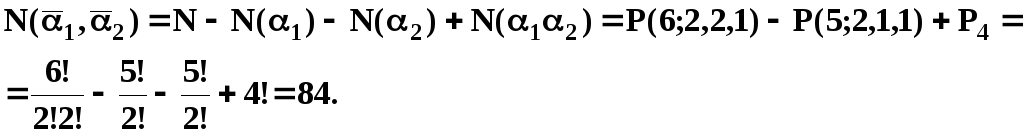
2. Скількома способами можна переставити цифри у числі 123 123 так, щоб ніякі дві однакові цифри не знаходилися поруч?

Розв’язання.

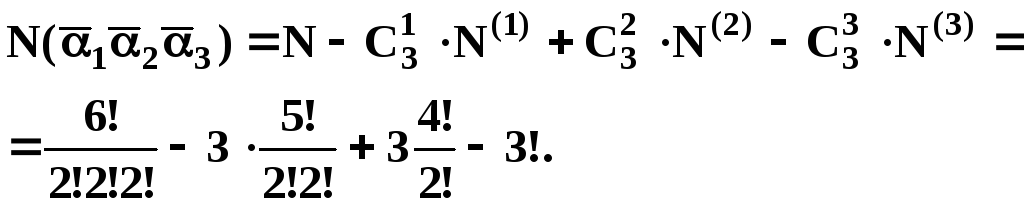
2. Пустелею йде караван із 5 верблюдів. Подорож триває багато днів і нарешті, усім набридає бачити попереду себе одного й того ж верблюда. Скількома способами можна переставити верблюдів так, щоб попереду кожного верблюда йшов інший, ніж раніше?

Розв’язання.

Завдання до лабораторної роботи

Відповіднодо заданого варіанту розв’язати задачі перерахунку.

Варіант №1.

1. Чоловік має6 друзів, і протягом 20 днів запрошуєдо себе 3 зних так, що компанія жодногоразу не повторюється. Скількомаспособами це можна зробити?

2. Скількомаспособамиіз колодиу 36 карт можна витягнути5 карт, серед яких2 з однаковиминомерами та 2 з однаковими, але іншиминомерами?

3. Із двох спортивних суспільств, в яких тренується по 100 фехтувальників, треба виділитипо одному фехтувальниковідля участів змаганні. Скількомаспособами можебути зроблений цей вибір?

4. У святах берутьучасть 12 дітей. У дідаМорозу є15 однакових подарунків. Скільки існує способів роздати дітям подарунки, якщо кожна дитина має отримати, хоча бпо одному дарунку?

5. Скількомаспособами можна посадити поруч3 англійців, 3 французів та3 турок так, щоб жоднітри співвітчизникине сиділи поруч?