Розміщення (- перестановки)

Розміщення ізпо–упорядкована послідовністьіз елементів множини, що містить всього елементів.

Два розміщення вважаються різними, якщо вони відрізняються:

– складом елементів;

– порядком розташування елементів;

– і тим, ідругим.

Наприклад.

Нехай є множина

Згенеруватиусі розміщенняіз3 по 2. Розміщенняіз3 по 2 для:

Два розміщення та – відрізняються порядком розташування елементів; та – відрізняютьсяскладом елементів;а та – і складом, і порядком розташування елементів.

Теорема 2

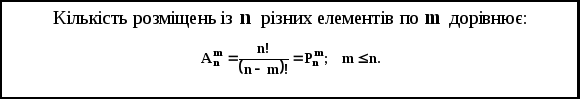
Примітка: при:

Доведення.

Нехай є різних об'єктів і їх необхідно розміститина різних місць. На 1-е місце є претендентів,на 2-е – претендент, на третє – , ..., на -е місце – претендентів. За правиломдобуткуотримаємо, що кількість різних розміщень із по складає:

Наприклад.

1) Скількома способами можна розставити на полиці 5 книг із 7?

Розв’язання.

Оскільки усі книжки різні, то нас цікавить і які книжки будуть розставлені на полиці, і у якому порядку:

.

2) Скільки різних чотирьохлітерних ідентифікаторів можна отримати, використовуючи літери алфавіту , якщо ні одна із літер не повторюється?

Розв’язання.

У алфавіті всього 5 літер, 4 із них вони повинні бути використані для генерування ідентифікатору, причому порядок літер у ідентифікаторі має значення:

Сполучення

Сполучення із по – набір з елементів множини, що містить різних елементів, без урахування порядку елементів у наборі.

Різні сполучення відрізняються один від одного тільки складом елементів, але не їх порядком.

Наприклад.

Нехай є множина

Згенерувати усі сполучення із3 по 2.

Сполучення із3 по 2 для:

Теорема 3

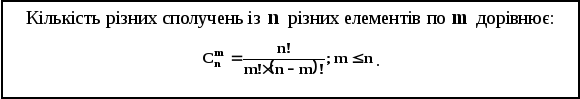
Доведення.

Кожне сполучення із елементів можна упорядкувати способами, тобто з нього виходитьперестановок. Дляусіх сполучень маємо перестановок, але цечисло дорівнює кількості різних розміщеньіз елементівпо, а отже, . Тоді, використовуючитеорему 2 маємо:

.

Властивості числа сполучень

1.

2. Симетричністьчисла сполучень:

3. Правило Паскаля

Для числа сполучень із посправедливе наступне рекурентне співвідношення:

.

4. БіномНьютона:

–біноміальні коефіцієнти.

При сума біноміальних коефіцієнтів дорівнює:

Наприклад.

1) Скількома способами із 25 членів наукового товариства можна обрати президію в кількості 3 осіб?

Розв’язання.

Оскільки треба обрати 3 осіб для роботи у президії наукового товариства, то порядок вибору значення не має, а має значеннятільки, які особи із 25 наявних увійдуть у склад президії. Тоді, число способів обрати президію у складі із 3 осіб дорівнює: .

2) Скількома способами із 25 осіб наукового товариства можна обрати президента, віцепрезидента та вченого секретаря?

Розв’язання.

У даному випадку має значення і склад обраних осіб, і порядок їх обрання, бо вони будуть мати різні повноваження. Перший із обраних буде президентом наукового товариства, другий – віцепрезидентом, а третій секретарем:

З другого боку, спочатку можна вибрати трьох осіб способами, апотім обчислити кількість способів роздати їм повноваження: . Оскільки мають значення і які особи обрані, і які повноваження кожен з них отримав, то за правилом добутку маємо

Третій варіант міркувань полягає у застосуванні тільки правила добутку. Президент наукового товариства може бути обраний способами. Після цього і незалежно від цього, віцепрезидент може бути обраний вжеспособами. Відповідно, секретар,способами. За правилом добутку маємо: .

2. На книжковій полиці розміщується томів книг. Скількомаспособами можна розставити їхтак, щоб татоми не стояли поряд?

Розв’язання.

Задача легше розв’язується через зворотну задачу. 30томів книгможна розставити на полиці без будь-яких обмежень способами. Обчислимо число способів розставити книжки так, що йтом будутьстояти поряд. Перший та другий том можна поставити поряд способами (або). Далі маємо розставити на полиціокремих томів та один складний об'єкт, що складається ізтатомів:.

За правилом добутку маємо рішення зворотної задачі:.

Тоді, пряма задача має наступний розв’язок:

.

3. Чотири стрілка повинні вразити8 мішеней(коженпо 2). Скількомаспособами вони можуть розподілити мішені міжсобою?

Розв’язання.

Для кожного стрілка має значення, які мішені йому будуть розподілені, але не має значення у якому порядку він буде в них стріляти. Тому, число варіантів вибору двох мішеней із 8 для першого стрілка дорівнює , для другого – , для третього відповідно –, для останнього –. За правилом добутку: .

4. Колода у карт містить 4 масті по карт у кожній.

Скількомаспособами можна вибрати:

1) 5 карт, 4 з яких з однаковими номерами?

2) три карти з одними номерами та 2 з іншими однаковими номерами?

Розв’язання.

1) Для того, щоб вибрати 4 карти із одним номером достатньо із наявних номерів вибрати один, а останню, 5 карту вибрати із колоди без 4 карт із цим номером:.

2) Для того, щоб вибрати 3 карти із одним номером треба спочатку вибрати один номер із існуючих, а потім із 4 карт з таким номером вибрати три карти:. Аналогічно вибираємо дві карти з однаковими номерами:, але номер вибираємо із варіанту.

Тоді, за правилом добутку.

5. Хор складається з 10 учасників. Скількома способами можна протягом 3-х днів вибирати по 6 учасників так, щоб кожен день були різні склади хору?

Розв’язання.

Порядок виступів важливий (який склад хору, в який день виступає),

,

не важливий:

.

5. Скількома способами можна переставити літери слова "паралелізм", щоб не змінювався порядок голосних?

Розв’язання.

Тема 2

З'єднання з повтореннями елементів

До цих пір розглядали підмножини із скінченних множин, що складаються з різних елементів. Часто на практиці мають місце випадки, коли серед розглянутих елементів є однакові. Тому вводять три типа аналогічних комбінаторних з'єднань, але з елементами, що поможуть повторюватися:

1) перестановки із повтореннями елементів;

2) розміщення із повтореннями елементів;

3) сполучення із повтореннями елементів.

Перестановки із повторенням елементів

Дана множина , що складається із елементів, у якій:

– елемент належить першомутипу;

– елементів належить другого типу елементів; ;

...;

– елементів належить -томутипу елементів.

Елементи одного й того ж типу не розрізняються між собою.

Специфікацією множини називається набір.

Теорема 1

Доведення.

Нехай – число різних перестановок з повтореннями у множині . Якщо б всі елементи множини були різні, то їх можна було б переставити способами.

Число меншеза у разів самеза рахунокперестановок елементівпершого типу, у – за рахунок елементів2 типу,та, ...,у – за рахунок елементів-того типу.

Слідство

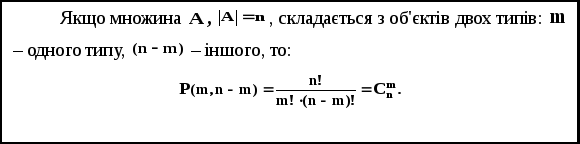
У загальному випадку:

Наприклад.

1) Скількома способами можна переставити букви в слові "каша"?

Розв’язання.

Усього в слові "каша" чотири літери, серед яких дві однакові:

2) Скільки різнихчисел можна отримати, переставляючи цифричисла 12341234?

Розв’язання.

У числі 8 цифр: дві – "1", дві – "2", дві – "3", дві – "4". За теоремою 1 маємо:

3) Скільки різних перестановок можна утворити з усіх літер слова «Міссісіпі»?

Розв’язання.

Всьогов слові9 букв, зних – 4 літери"і", три літери"с", одналітера"м" та одналітера"п".

.

4) Тридцять осіб розбиті на 3 групи по 10 чоловік у кожній. Скільки різних складів груп можна скласти?

Розв’язання.

Задача може бути розв’язана двома способами, що випливає із слідства до теореми про перестановки із повтореннями.

Порядок входження людей до груп не має значення. Тоді, спочатку, вибираємо десять чоловік із тридцяти, що увійдуть у першу групу. Це можна зробити способами. Потім, із двадцяти тих, що лишилися, вибираємо десять чоловік для другої групи, й останні десять складуть третю групу. За правилом добутку, маємо:

.

Другий спосіб слідкує із безпосереднього застосування логіки теореми про перестановки із повтореннями. Розбиття тридцяти чоловік на три групи можна отримати наступним чином. Взяти усі перестановки тридцяти чоловік: та виключити з них перестановки перших десяти: , бо вони усі увійдуть у першу групу і перестановки їх між собою враховувати не треба (тобто вони в цьому сенсі вважаються однаковими). Потім аналогічно, виключити перестановки другої десятки та третьої. Тоді, кількість перестановок із повтореннями із специфікацієюдорівнює:

.